仓库源文，站点原文

layout: post title: 【整理】APBS教程 categories:

• 科 tags:
• gmx math: true

• 2017年03月12日 20:57:37

【按】在算MM/GBSA或MM/PBSA时可能会用到APBS程序. 网上有一个此程序低版本文档的翻译, APBS教程. 翻译得不够专业, 也不大通顺, 但大致可以作为入门资料. 我对这份文档稍加整理, 希望对将要使用APBS的人有所帮助. 大致而言, 对要使用APBS做静电势能表面图的人, 参考文档前三章足够了; 对要计算自由能的人, 参考4-7章; 最后几章用到的人少, 文档也不详细, 仅作参考.

1. 怎样阅读教程

本教程是以"怎样做"的形式设计的, 使读者能熟悉使用APBS进行静电计算. 读者需要最新版本的APBS来练习本教程中提供的实例.

重要信息 注意本教程中的许多实例操作也可以通过网络Gemstone实现, 而不需要在本地安装APBS软件. 更多信息见 第10章 怎样通过网络运行APBS? (Gemstone).

提示 本教程仍在完善之中, 并且会在下一版本的APBS发布之前完成. 未完成部分涵盖的许多课题在APBS实例目录中有所展示.

2. 怎样准备结构进行静电势计算

为了对你关注的生物大分子结构进行静电计算, 你需要向APBS提供每个原子所带电荷及原子半径等信息. 电荷用来为求解泊松-波尔兹曼(PB)方程提供生物分子的电荷分布, 半径则用来构建电介质和离子的可及度函数. 电荷和半径信息可由不同的文件格式提供给APBS, 下面对此进行详细阐述.

2.1 PQR格式

PQR格式提供了一种添加参数信息的简单方式: 将PDB格式结构文件中的occupancy和temperature列以电荷(Q)和半径(R)代替. 然而, 这种格式的简单性也限制了它的可扩展性: 如果不借助使用其它软件如PDB2PQR, 向一般的格式中添加新的原子形式和参数是非常困难的. 下面介绍的XML格式则要容易修改得多.

2.2 XML格式

XML格式提供了一个添加参数信息的复杂格式, 但同时在格式化, 可扩展性和其它修改方面具有更大可能性. 正如在PQR格式中, 原子坐标被补充以电荷和半径信息. 完整的格式说明请见APBS用户手册.

2.3 由PDB文件生成PQR文件(PDB2PQR)

注意 本教程适于运用 PDB2PQR 1.2.1

PDB2PQR网络服务和软件可将绝大多数PDB文件转换成PQR格式, 同时生成一些"警告"信息, 特别是不能对大量缺失原子的坐标进行"修复". 虽然PDB2PQR能修复某些侧链中缺失的重原子, 但目前它不能建模大范围缺失的骨架和侧链坐标.

PDB2PQR也可进行氢键优化, 侧链旋转异构体搜索, 附加限定的滴定状态, 设定配体参数和准备APBS输入文件等. 详细内容见APBS用户手册.

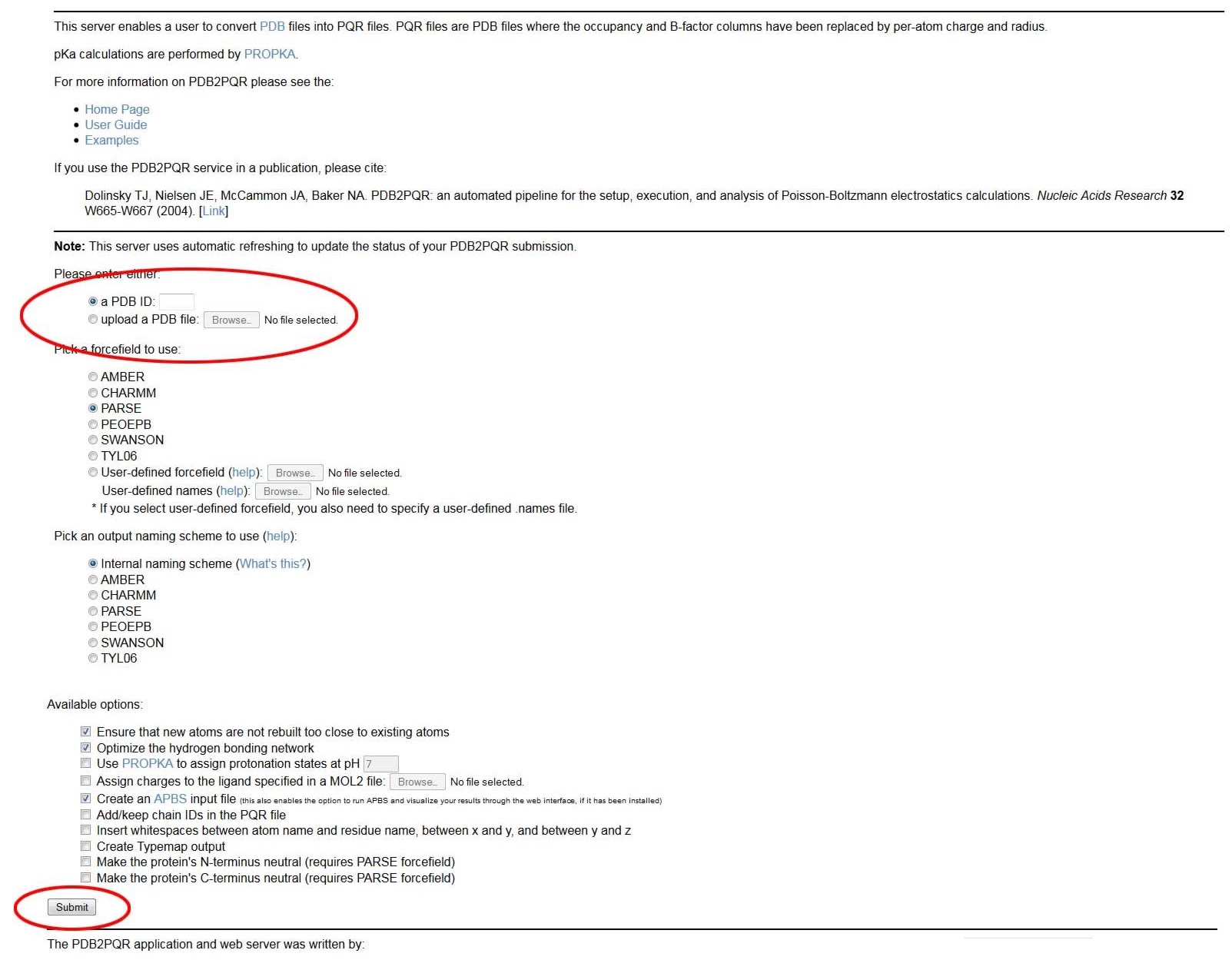
PDB2PQR在PDB2PQR主页中进行了详细讨论. 因此, 我们这里简略地回顾由PDB文件生成PQR文件的所需步骤. 首先, 打开PDB2PQR网络服务器.

2.3.1 选择要转化的PDB文件

输入四个字符的PDB ID或编号(如1FAS, 1MAH, 1LYS等)或者是上传自己的PDB文件均可.

注意 如果你选择输入四个字符的PDB文件, PDB2PQR将对所有PDB文件中的链进行转换, 因为它结晶于PDB中(比如, 对所有相关的进行转换而不仅是生物单元).

2.3.2 选择力场

大多数情况下, 这个选择是简单的: PARSE. 该力场经过了优化适用于隐式溶剂计算, 而且可能是蛋白质静电势能和许多一般形式的能量计算可视化处理的最佳选择. 然而, AMBER和CHARMM在某些情况下更合适, 比如想与用这些力场进行的模拟做比较, 需要有核酸的力场, 想利用这些力场对配体进行参数化等.

上传自定义力场也是可行的(比如, 对配体或不常见残基进行半径和电荷定义). 详细信息见PDB2PQR手册.

2.3.3 输出命名设置

这基本与静电计算无关, 但对可视化至关重要. 在不确定时, 选择Internal naming scheme, 使其与IUPAC标准一致.

2.3.4 其它选择

这些选择可分为两类: 怎样在结构上构建缺失原子(包括氢原子)和附加输出设置.

最后下载生成的pqr文件

3. 怎样观察生物大分子周围的静电势

有许多极好的分子可视化软件可用来观察生物分子的静电性质. 由于这样的程序太多, 我们将主要介绍三个我们熟悉的软件包.

3.1 VMD

VMD分子可视化软件包支持运行APBS计算并对得到的静电势能结果进行可视化处理. VMD开发者提供了APBS插件. 作为补充, 我们将展示怎样在VMD中利用APBS从PDB文件得到结构和静电势能图.

注意 本教程基于VMD 1.85. 部分图片取自VMD配合APBS显示分子表面静电势.

3.1.1 生成PQR

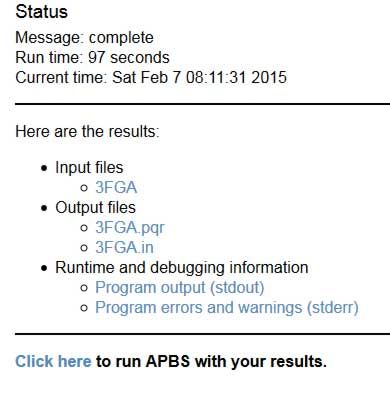
我们以ARC(PDB ID 1MYK)为例, 它是一个DNA结合蛋白. 可视化过程的第一步是为VMD和APBS生成PQR文件. 请参见2.3 由PDB文件生成PQR文件(PDB2PQR).

3.1.2. 载入PQR

在VMD中载入刚生成的PQR文件(在VMD主窗口中选择File→New molecule...). 调整分子, 使其以你所希望的方式显示. 根据你在PDB2PQR中运用的力场不同, 你可能会在VMD中看到一些奇怪的成键. 当载入PQR文件时, 键的长度是由PQR半径推得的. 这些半径与连续静电计算有关, 而与可视化无关. 不必担心会出现一些奇怪的成键(可隐藏氢原子以达到更好的视觉效果).

3.1.3 运行静电计算

现在已经为静电计算做好了准备

1. 在VMD主窗口中选择Extensions→Analysis→APBS Electrostatics. 此时弹出一个APBS Tool窗口.
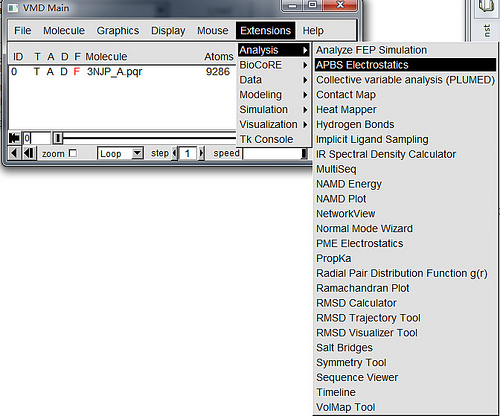
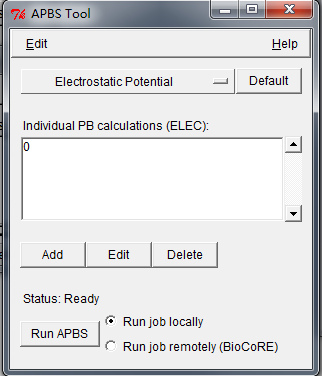
2. 在APBS Tool窗口左上角选择Edit→Settings..., 修改工作路径(计算结果保存路径), 指定APBS程序所在路径. 点击OK关闭此窗口. 注意, 此设置无法保存, 每次运行都要重新设置.
3. 从Individual PB calculations (ELEC):窗口选择0. 单击Edit按钮. 根据需要调整APBS计算设置. 默认设置一般可行, 然而修改Mobile Ions来调整计算时的离子强度也是有用的. 完成后单击OK.
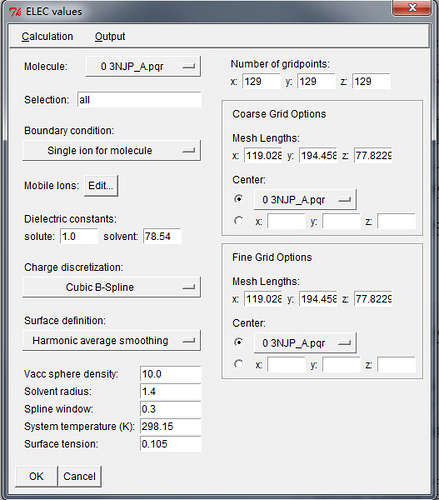
4. 现在已经准备好了运行计算. 在APBS Tool窗口中单击Run APBS. 打开VMD终端窗口察看运行计算时返回的信息. 计算完成后会出现一个APBSRun: Load APBS Maps窗口. 选择Load files into top molecule, 然后单击OK将APBS的计算结果会加载到打开的分子中. 这时, VMD主窗口中分子的Vol项应该为1, 表示里面有一组格点数据.

3.1.4 静电可视化

3.1.4.1 等势面可视化

最常用的可视化方法之一就是绘制等势面.

1. 首先, 在VMD主窗口中选择Graphics→Representations....
2. 单击Create Rep按钮, 创建新的图层, 改变Drawing Method至Isosurface.
3. 将Draw由Points改至Solid Surface, Material改至Transparent.
4. 注意现在isovalue值是0; 根据个人使用偏好, 改变它至1(或5, 10等).
5. 若沿用静电势能着色的标准传统, 在Coloring Method中选择ColorID 0.
6. 对于负值等势面, 单击Create Rep, 选择新创建的图层. 改变isocontour值至-1(或5, 10...), ColorID改至1.

这时, 你得到的图像将类似下图(注意, 为使得图像更加清晰我们将Drawing Method由表面改为了点状)

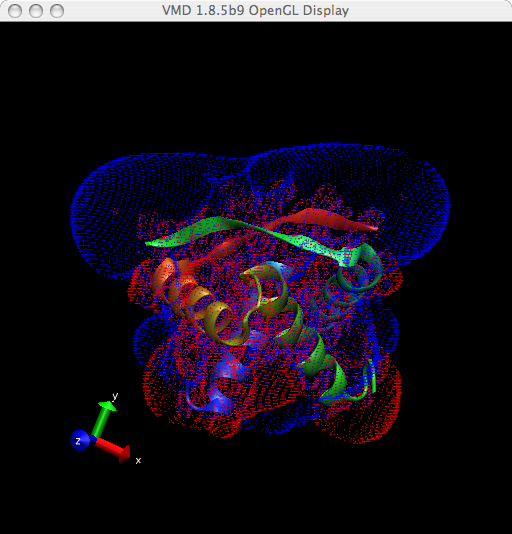
图 3.1. VMD显示的ARC等值面

3.1.4.2 表面势能可视化

静电势能可视化的另一个常用方式是将静电势能映射到生物分子的表面. 开始之前, 在VMD图形窗口中用Delete Rep来删除刚才创建的两个等势面图层.

1. 在图形窗口(从VMD主窗口中选择Graphics→Representations...)中使用Create Rep按钮创建新的图层.
2. 在Drawing Method标签下改变绘图方式至Surf¹, Coloring Method改至Volume.
3. 在Trajectory标签下改变Color Scale Data Range:至-10到10(或其它偏好的值).
4. 基于你所使用的VMD版本和个人偏好, 你可能想改变图像的颜色映射方式. 在VMD主窗口中选择Graphics→Colors..., 然后在弹出的颜色控制窗口中选择Color Scale标签. 传统的静电着色设置是RWB(在Method菜单中).

现在, 你的分子看起来应该如下图所示:

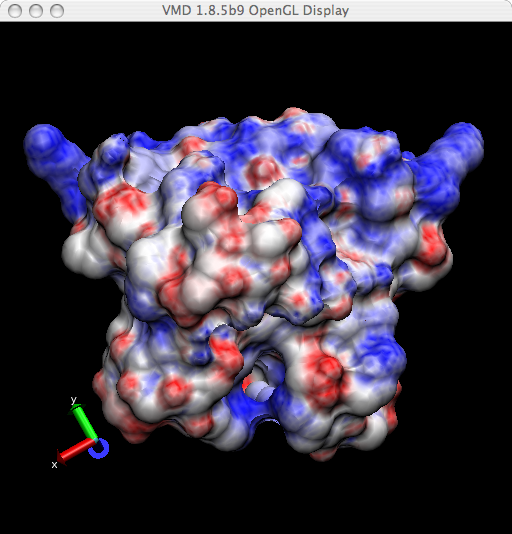
图 3.2. VMD显示的ARC表面静电势

3.2 PyMOL

PyMOL分子可视化软件包同样支持运行APBS计算和对得到的静电势能结果进行可视化处理. 我们将展示怎样在PyMOL中利用APBS从PDB文件得到结构和静电势能图

注意 本教程基于PyMOLX11Hybrid 0.99. 部分图片取自用PyMOL查看蛋白质表面静电势.

3.2.1 生成PQR文件

我们将以fasciculin-2(PDB ID 1FAS)为例, 它是一种能结合到带负电的乙酰胆碱酯酶上的蛇神经毒素. 请参见2.3 由PDB文件生成PQR文件(PDB2PQR)来生成PQR文件.

在PyMOL中载入生成的PQR文件(File→Open...), 选择你喜欢的显示方式.

3.2.2 进行静电计算

点击Plugin→APBS Tools...打开APBS计算插件, 出现PyMOL APBS Tools窗口.

1. 在Main标签下, 选择Use another PQR, 然后搜索所需PQR文件(通过Choose Externally Generated PQR:按钮)或直接输入PQR文件的路径. 这一步是必须的, 它保证了你使用的是PDB2PQR所赋予的半径和电荷.
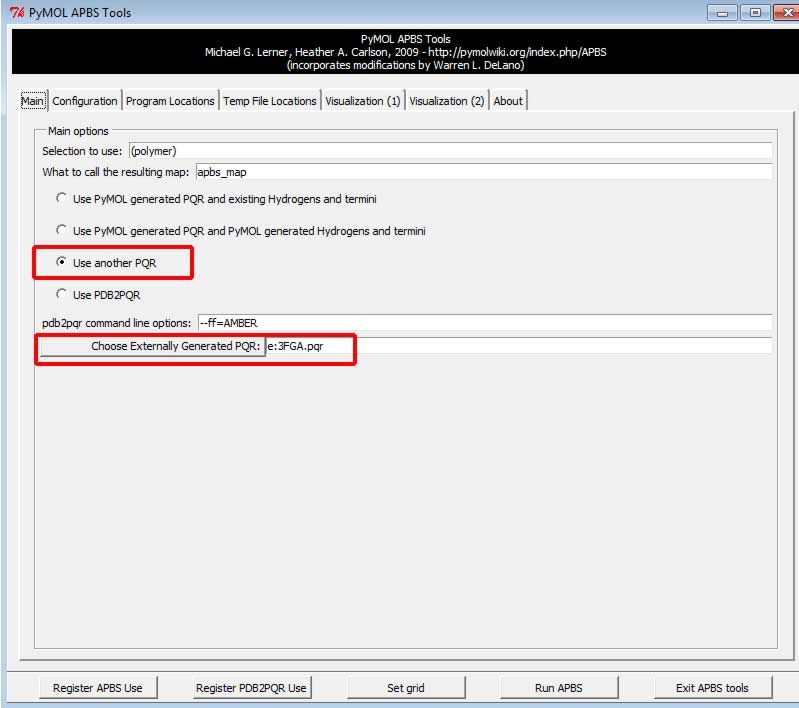
2. 在Program Location标签下, 指定APBS程序的路径(通过APBS binary location:按钮)或直接输入其路径. 对大多数生物分子来说APBS psize.py location:项无须设置.
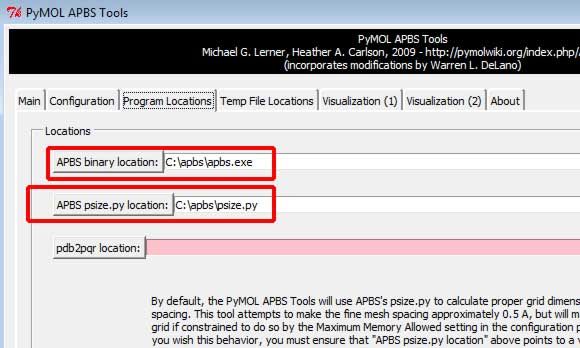
3. 在Temporary File Locations标签下, 设置在计算过程中生成的各种文件的路径. 如果你想保留生成的文件以待后用, 这一步十分必要.
4. 在Configuration标签下, 单击下方的Set grid进行空间格点设置. 默认设置对除高度荷电的分子外一般都是适用的.
5. 在Configuration标签下, 设置其余的参数, 默认值通常是可行的.
6. 在Configuration标签下, 单击Run APBS按钮开启APBS计算. 根据计算机的运算速度, 计算可能需要几分钟时间. 计算结束后Run APBS按钮变灰.

3.2.3 静电势能可视化

在进行下面的操作之前, 你需要将静电势能数据载入PyMOL. 在PyMOL APBS Tools窗口Visualization标签下, 点击Update按钮.

3.2.3.1 静电势能等势面

PyMOL可轻松进行此操作: 调整正电和负电"等势"面至所需值(通常是+/- 1, +/- 5或+/- 10 kT/e), 在Positive Isosurface, Negative Isosurface框中单击Show按钮.

这时, 你将得到如下所示图形:

图 3.3. PyMOL显示的FAS2 +/- 1 kT/e 静电势等值面

3.2.3.2 表面势能

如果没准备好, 你可以通过点击Positive Isosurface, Negative Isosurface和Hide按钮来隐藏等势面.

表面势能也可直接看到. 在Molecular Surface框中设置Low和High至所需值(通常是+/- 1, +/-5或+/-10 kT/e), 表面被以红色(-)或蓝色(+)着色. 选中Solvent accessible surface和Color by potential on sol. acc. surf.按钮来在溶剂可及(probe-inflated or Lee-Richards)表面上绘制势能图². 单击Show按钮载入表面势能.

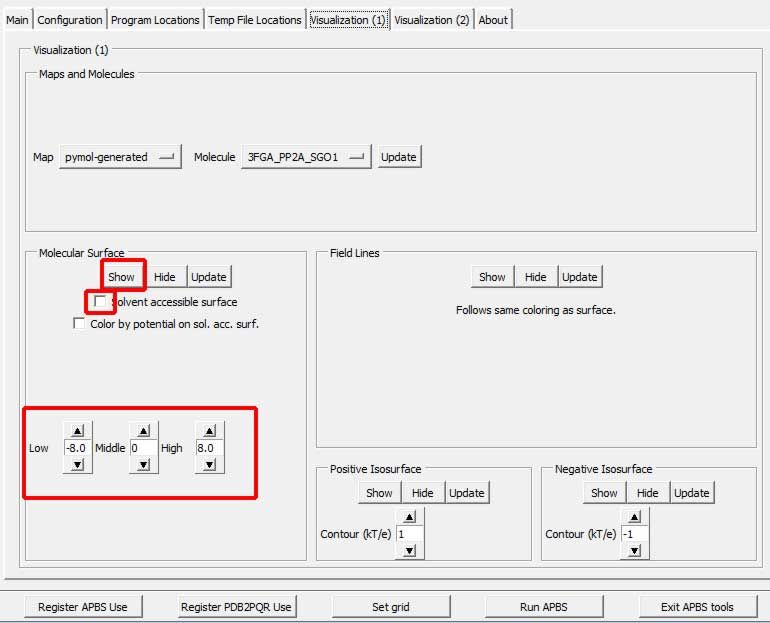
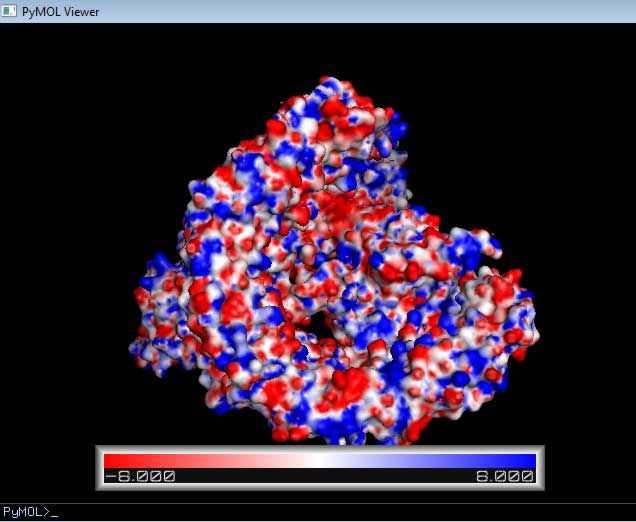
图 3.4. PyMOL显示的FAS2 +/- 5 kT/e 表面静电势能

4. 怎样计算溶剂化能?

溶剂化能通常被分解成自由能循环, 如图4.1. 注意此类溶剂化能通常对应于固定构象; 由此, 它们应确切地被称为"平均力的势能". 在下面的章节中会详细介绍怎样将APBS计算应用于这样的循环中的极性和非极性部分.

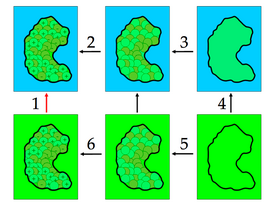
图 4.1 全溶剂化能循环. 这个循环将许多过程组合在一起得到溶剂化能(步骤1). 步骤2表示溶剂中溶质的充电过程(例如, 非均匀介质, 有离子存在). 步骤3表示引入相吸引的溶质-溶剂的扩散作用(例如, 在溶剂可及空间的Weeks-Chandler-Andersen作用积分). 步骤4表示引入相排斥的溶质-溶剂相互作用(例如, 孔道形成). 步骤5和6基本是无用的, 虽然它们可以用来补偿在步骤3和步骤4中加入的不想要的能量. 最后, 步骤6表示在无可移动离子真空或均一介质环境中溶质的充电过程.

4.1 极性溶剂化

图4.1 中的全自由能循环通常被分解成极性部分和非极性部分. 极性部分通常以步骤2和步骤6中的充电能表示:

$$\D_p G=\D_2 G - \D_6 G$$

APBS静电计算返回的能量是充电自由能. 因此, 要得到极性部分对溶剂化自由能的贡献, 我们仅需启动与图4.1 中步骤2和步骤6相对应的两项计算即可. 然而, APBS返回的充电自由能包括自相互作用部分. 即因自身电荷分布相互作用产生的能量. 这些自相互作用能通常很大, 且对离散化(格点分布, 位置等)中出现的问题特别敏感. 因此, 一定要在格点分布, 长度和中心相同的设置下进行这两项计算, 以保证能精确地抵消自相互作用能项.

玻恩离子是极性溶剂化的一个典型例子: 非极性的球中间有一个电荷, 电荷周围是水介质. 在不存在外部离子的情况下, 该体系的极性溶剂化能由以下方程给出:

$$\Dp G\text{Born} = {q^2 \over 8\p \ve0 a} \left( {1\over\ve\text{out} } -{1\over \ve_\text{in} } \right)$$

方程4.1 玻恩离子的极性溶剂化能. $q$ 为离子电荷, $a$ 为离子半径, 两个 $\ve$ 表示内部和外部(溶剂)的介电常数. 这个模型假定离子强度为0.

为使用APBS, 我们可以为玻恩离子创建一个PQR文件.

例 4.1. 玻恩离子 PQR

我们关注在均一和非均一介电系数下进行两项APBS充电自由能计算. 我们假定内部介电常数是1(真空), 外部介电常数是78.54(水). 这样设置后, 极性溶剂化能的表达式具有以下形式:

$$\Dp G\text{Born} = {-685.83\over R} \;\AA\ \text{kJ/mol} $$

$R$ 表示半径, 以埃为单位. 进行计算所需的APBS输入文件如下

例 4.2. 波恩离子输入文件

用最新版本的APBS运行这个例子给出的结果是-229.59 kJ/mol, 这与由上面的解析方程给出的结果-228.61 kJ/mol是非常一致的.

注意上面玻恩离子的例子可以轻松地推广到其它的极性溶剂化能计算. 比如, 可以将离子加到solv ELEC区, 可以修改介电常数, 可以改变表面定义(在ELEC区均可!), 或者可试着应用于更加复杂的分子. APBS里的许多例子(比如, solv和ionize)也运用了溶剂化能计算.

注意 随着分子变的更大, 考察得到的溶剂化能值对格点空间分布和尺寸的敏感程度是很重要的.

4.2 非极性溶剂化

在图4.1 的全自由能循环中, 非极性溶剂化自由能通常以步骤3到步骤5的能量变化表示:

$$\D_n G=(\D_3 G-\D_5 G)+\D_4 G$$

步骤4表示在溶剂中构建一个孔穴的能量, 步骤3-5是与溶质, 溶剂之间扩散作用相关的能量. 有许多选择可以用来模建非极性溶剂化过程. APBS实现了一个相对通用的模型, 此模型是由Wagoner和Baker(PNAS 2006)提出的, 可供参考. APBS用户手册详细说明了此模型的实现和调用.

我们关于孔穴构建项(步骤4)的基本模型是受定标离子理论的启发, 它具有下面形式:

$$\D_4 G=p\D V+\g \D A$$

其中, $p$ 是溶剂压强(APBS中的press关键词), $\D V$ 是溶质的溶剂可及体积, $\g$ 是溶剂表面张力(APBS中的gamma关键词), $\D A$ 是溶质的溶剂可及表面面积.

我们关于扩散项的(步骤3和步骤5)基本模型遵循了Levy, Zhang, Gallicchio(J Comput Chem, 2002)提出的Weeks-Chandler-Anderson框架:

$$\D_3 G-\D5 G=\r \int\W u^\text{(att)} (y)\q(y) \rm d y$$

其中 $\r$ 是溶剂密度(APBS中的bconc关键词), $\W$ 是问题域, $u^\text{(att)}(y)$ 表示在 $y$ 点溶质, 溶剂相吸引的扩散作用, 其中的Lennard-Jones扩散参数是由APBS参数文件定义的, $\q(y)$ 描述 $y$ 点的溶剂可及程度.

注意 Press, gamma, 和bconc值可单独调整意味着上面提到的通用非极性溶剂化模型可轻松应用于其它常见的非极性溶剂化模型. 比如, 将press和bconc设为0将会产生一个典型的溶剂可及表面积模型.

与玻恩离子不同, 没有简单的例子来展示这些类型的非极性计算. APBS包括许多用上面的非极性模型进行计算的例子. 感兴趣的读者可考察APBS提供的非极性烷烃的例子.

5. 怎样计算结合能?

一般地, 隐式溶剂模型被用来计算溶剂化对结合自由能的贡献. 其余对结合自由能的贡献(分子势能, 熵变等)必须单独计算, 本教程并未对其进行讨论. 唯一例外的是本教程包括了分子间库仑作用; 下面我们将讨论这些能量在APBS中怎样计算.

我们计算溶剂化对结合自由能贡献的框架如图5.1

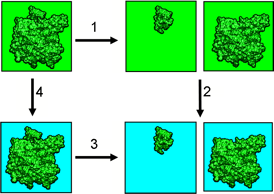
图5.1 结合自由能循环. 展示了从均一介质环境(相互作用由库仑定律描述)到非均一介质环境的结合自由能, 其中非均一介质环境具有不同的内部(绿色)和外部(青色)介电常数. 结合(解离)自由能由步骤3描述.

结合自由能由以下方程给出

$$\D_\text{bind} G =-\D_3 G=\D_4 G -\D_1 G-\D_2 G$$

方程 5.1 基于图5.1的结合自由能方程

以下章节将对怎样计算方程中的各项进行详细说明.

5.1 溶剂化能对结合能的贡献

如果仅关注计算溶剂化对结合能的贡献(图 5.1中第4步和第2步), 我们只需按照4. 怎样计算溶剂化能?的说明计算复合和分离组分的溶剂化能. 那么, 溶剂化能对结合的贡献由以下方程给出:

$$\alg \D \D_\text{solv} G &=\D_4 G -\D2 G \ &=\D\text{solv} G\text{complex} -\D\text{solv} G\text{mol 1} - \D\text{solv} G_\text{mol 2} \ealg$$

方程 5.2 在由mol 1和mol 2组成的双组分复合物中, 溶剂化对结合自由能的贡献. 编号参见图 5.1

溶剂化的贡献可以分成极性和非极性两部分, 正如4. 怎样计算溶剂化能?中提到的.

5.2. 包含库仑力的贡献

为得到完整的结合自由能循环(见图 5.1), 我们需要在溶剂化能差值的基础上增加分子间的库仑力贡献以得到静电/溶剂化对结合自由能的全部贡献. 特别地, 我们对结合过程中库仑静电势能的变化很感兴趣, 它由以下方程给出:

$$\alg \D \D_\text{coul} G &= -\D1 G \ &= \D\text{coul} G\text{complex}-\D\text{coul} G\text{mol 1}-\D\text{coul} G_\text{mol 2} \ealg$$

方程5.3 在由mol 1和mol 2组成的双组分复合物中, 库仑力对结合自由能的贡献. 编号见方程 5.1

方程 5.3中每个 $\D G\text{coul}$ 的值是在统一介电常数下分子(或复合物)中所有原子两两之间库仑作用的总合和. 为了能将这些库仑贡献与上面提到的溶剂化能相结合, 必须保证在计算库仑贡献时使用了一致的介电常数. 特别地, 库仑作用计算时使用的一致介电常数必须以溶剂化能计算时的状态作为参考态. 比如, 如果溶剂化能计算的是蛋白质由统一介电常数为 $\ve{in}$ 的介质转移到内部介电常数是 $\ve{in}$, 外部介电常数是 $\ve{out}$ 的介质, 库仑力能必须在介电常数为 $\ve{in}$ 下计算. APBS附件coulomb就是用来进行这些单分子库仑势能计算的. 将PQR文件作为输入文件, coulomb程序将在真空电介质(比如统一介电常数为1)下计算库仑力能. 如果参考介电常数是 $\ve{in}$, 那么所有coulomb返回的能量需要除以 $\ve_{in}$.

在使用恰当的介电常数 $\ve_{in}$ 来计算库仑结合能的情况下, 静电/溶剂化总自由能可通过方程 5.1-5.4算得

$$\D\text{bind} G =\D\D\text{solv} G +\D\D_\text{coul} G$$ 方程5.4. 结合自由能

5.3 不行! 配体没有设置参数!

PDB2PQR现在已经能为配体设置参数了(1.2.0版), 这要感谢Jens Nielsen小组的协作. 详细信息请参见PDB2PQR主页.

5.4 一个配体结合的例子

警告 未完成

6. 怎样计算溶剂化力?

APBS提供对极性和非极性溶剂化过程中力的计算, 步骤与4. 怎样计算溶剂化能?一样. 一般地, 力可通过修改溶剂化能计算时使用的输入文件获得, 添加calcforce total可获得溶质分子整体受力而添加calcforce comps可获得每个原子受力的详细信息. 需要注意的是, 正如计算溶剂化能, "自身作用"项必须移除(参考例 4.2).

7. 怎样计算pKa?

重要信息 本教程由Dave Sept提供, Dave Sept是一个生物分子模拟实验室的成员之一.

7.1 概况

为什么计算pKa? 虽然用来展示连续静电概念不是pKa计算的常规应用, 但它具有重要的科研和教学价值. 从科研的观点来看, pKa值是生物分子(特别是酶)功能的重要决定因素, 并且它可以用来评定功能活动和确定活性位点. 从教学的角度来看, pKa计算需要所有重要的连续静电学概念, 因此可联系到溶剂化和结合能.

注意 本教程包括测定生物分子pKa值的Poisson-Boltzmann方法. 其余测定pKa和滴定状态的方法在PDB2PQR示例中给出. 如果将用这些方法得到的结果与PDB2PQR结果作比较, 将会发现更多乐趣.

7.2. 介绍

下面是对生物分子pKa和滴定状态相关概念的简洁介绍. 更多的信息可参阅大多数的生物化学和生物物理教科书或一些关于pKa的原始文献³.

回顾可知, 酸解离常数Ka描述了酸解离成其组分的过程:

$$\ce{HA <=>[K_a] H^+ + A^-}$$

采用活度的方式

$$Ka={a{\ce{H}^+} a{\ce{A}^-} \over a\ce{HA} }$$

在"理想状态"下⁴, 活度可以被浓度代替

$$Ka={c{\ce{H}^+} c{\ce{A}^-} \over c\ce{HA} }$$

你应仍能记得化学平衡常数可由以下方程与自由能联系在一起

$$-RT \ln K_a = \Da G=G\ce{HA}-G{\ce{H}^+}-G{\ce{A}^-}$$

然而, 化学家发现用以10为基数的对数比用自然对数来衡量pH更简单, 因此, pKa被定义为:

$$\text{p}Ka=-\log{10}(K_a) =-\lg K_a=-{\ln K_a \over \ln 10}={\D_a G \over RT \ln 10} \approx {\D_a G \over 2.303 RT}$$

7.2.1 氨基酸模型pKa值

在许多计算中, 基于模型值来赋予氨基酸侧链的pKa 值, 以此

$$\ce{HA(aq) <=>[K_a^\text{model}]H^+(aq)}+\ce{A}^-\ce{(aq)}$$

来模拟溶剂中的单氨基酸. 许多模型pKa值在下表中列出:

在下面的章节中我们将看到, 这些模型值为计算蛋白质pKa值提供了基础.

7.2.2 蛋白质pKa值

上面章节提到的模型pKa值是将所有质子化的化学复杂性(成键和断键)转移到模型值中. 特别地, 蛋白质pKa值是以模型化合物的微扰来计算的, 正如下面的自由能循环.

蛋白质环境中氨基酸的pKa由下面的自由能循环给出

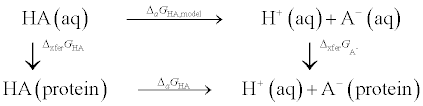
在下式中, 我们对于从已知的模型 $\Da G\text{HA,model}$ 值得到未知的 $\Da G\text{HA}$, 以及未知的 $\D\text{xfer} G\text{HA}$, $\D\text{xfer}G{\text{A}^-}$ 是十分关注的:

方程7.1 酸解离自由能

$$\alg 0 &= \Da G\text{HA, model} +\D\text{xfer} G{\text{A}^-} -\Da G\text{HA}-\D\text{xfer} G\text{HA} \ \Da G\text{HA} &= \Da G\text{HA, model} +\D\text{xfer} G{\text{A}^-} -\D\text{xfer} G\text{HA} \ealg$$

一般地, $\D\text{xfer} G\text{HA}$ 和 $\D\text{xfer} G{\text{A}^-}$ 的值由计算模拟获得. 按照一定的方案, 几乎每一个自由能计算方法都可用来获取这些能量. 在这个方案中, 带电的和不带电的氨基酸的溶剂化(去溶剂化)能是按照下面来计算的:

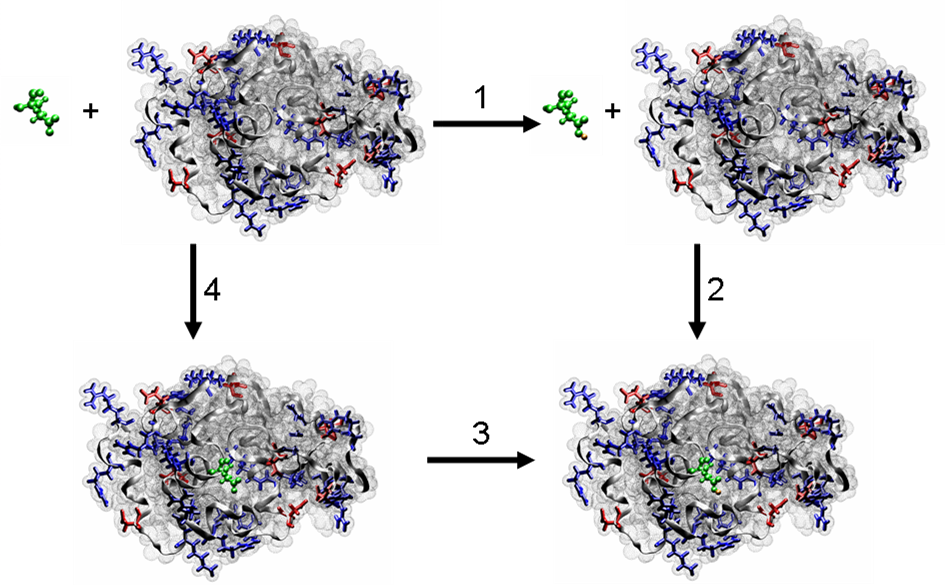
图 7.1. pKa微扰自由能原理图

注意这些能量在计算中假定了具有相同的背景状态; 换句话说, 在氨基酸带电和不带电状态这个问题上, 蛋白质中其它的可滴定基团也采用了相同的状态. 稍后我们会讨论这个假设的含义.

7.2.3 蛋白质pKa计算的连续静电方法

虽然几乎任何自由能方法都可以用来计算将质子化和未质子化的氨基酸从溶剂转移到蛋白质环境时的能量, 但连续静电方法(通常)是一个在精度和计算效率上令人满意的折衷方法.

需要计算的迁移自由能, $\D\text{xfer} G\text{HA}$ 和 $\D\text{xfer} G{\text{A}^-}$, 可从Poisson-Boltzmann(PB)能量决定. 特别地, 这些能量可作为有效的"结合能计算"来进行计算, 与APBS示例和教程中的能量计算相似:

$$\D_\text{xfer} GX = G\text{protein with charged X}-G\text{protein with uncharged X}-G\text{charged X in solution}$$

方程7.2. 迁移自由能

其中

• $G_\text{protein with charged X}$ 是蛋白结合了基团 $X$ 的静电能, 其中基团 $X$ 上的所有电荷设为正常值.
• $G_\text{protein with uncharged X}$ 是蛋白结合了基团 $X$ 的静电能, 其中基团 $X$ 上的所有电荷设为0.
• $G_\text{charged X in solution}$ 是溶剂中基团 $X$ 的静电能, 其中所有电荷设为正常值.

注意, 与结合能一样, 方程7.2可有两种方式来衡量:

衡量迁移自由能的方法

• 直接在PB方程中, 计算各个状态下PB计算结果减去总静电能(包括自身作用能)值. 为了使得这项工作能进行, 在每一个PB计算中所有构象/格点位置/电荷状态必须相同.
• 间接地, 可通过溶剂化自由能的PB计算和静电相互作用能的库仑定律计算(在介电常数为 $\ve_p$ 下)实现. 对于一个好的有效格点设置, 这个方法更稳定.

通过自由能循环, 两种方法都可以给出所需的 $\D_\text{xfer} G_X$. 然而, 考虑到所有计算都使用了相同的格点和构象, 使用总静电能的直接方法通常是最有效的.

注意, 上面讨论的两种方法都没有明确地允许在我们研究的酸性基团质子化/去质子化的过程中可以改变蛋白质中其它基团的滴定状态. 另外, 这两种方法都没有明确地提供与质子化/去质子化相伴随的蛋白质构象变化. 因此, 用这种方法我们不能计算真实的pKa值. 我们计算的是内禀pKa值.

7.3 应用于溶菌酶

7.3.1 背景

鸡蛋白溶菌酶(HEWL)是pKa计算的常用的体系, 因为它的可滴定残基有许多有意思的值. 关于此酶pKa的早期研究工作可参见Tanford C, Roxby R. Interpretation of protein titration curves. Application to lysozyme. Biochemistry. 11(11), 2192-8, 1972, 其中也有这个实验室使用的pKa值. 更多关于近来的pKa计算和许多方法的综述可见Nielsen JE, Vriend G. Optimizing the hydrogen-bond network in Poisson-Boltzmann equation-based pk(a) calculations. Proteins-Structure Function and Genetics. 43(4), 403-12, 2001. 最后, 溶菌酶的生物相关性在Wikipedia中作了简要概述.

HEWL有两个活性位点残基, 即GLU 35和ASP 52. 它们的滴定状态决定了酶的催化能力:

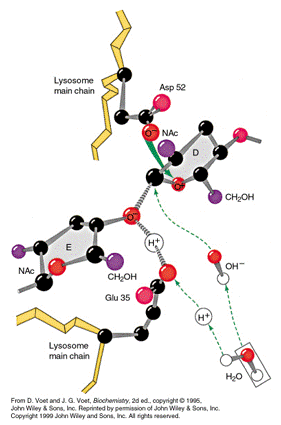
图 7.2. HEWL的活性位点

特别地, 只有在ASP 52离子化(pKa≈1.2)和GLU 35呈中性(pKa=6.3)的情况下HEWL才有活性.

另外, 溶菌酶中ASP 66的pKa值是6.6, HIS 15的pKa值是5.7.

7.3.2 概况和声明

下面, 我们将演示确定GLU 35内禀pKa的步骤. 然而, 这项工作实际上不能很好地完成(你需要找到原因!). 因此, 对HIS 15和ASP 66你也需要进行相同的操作, 以获得计算连续溶剂pKa的更好示例.

7.3.3 准备PDB文件

从PDB下载2LZT, 以2LZT-GLU35.pdb保存. 如果你有时间, 你也应该访问PDBSum分析页面以获得更多关于结构的信息.

水分子会出问题! 在继续操作之前, 将PDB中所有水分子移除. 这是非常重要的.(为什么?)

为进行pKa计算, 我们将需要获得GLU 35质子化的形式. 我们将通过PDB2PQR网络服务器来实现. PDB2PQR可进行一系列操作来"整理"PDB文件, 使其适于静电计算. 这些操作在PDB2PQR主页中做了描述.

如果没有特定要求, PDB2PQR会基于模型pKa值向残基上加氢. 因此, 我们需要将谷氨酸残基名由GLU改为GLH, 这样就指定了GLU 35的滴定状态. 可使用你喜欢的文本编辑器进行修改, 将结果以2LZT-GLH35.pdb保存.

现在我们准备好了运行PDB2PQR, 来使我们的PDB文件变为质子化的形式. 使用命令行版本的PDB2PQR或者PDB2PQR主页列出的网络服务器来生成2LZT-GLU35.pdb和2LZT-GLH35.pdb的质子化PQR文件. 将结果分别命名为2LZT-GLU35.pqr和2LZT-GLH35.pqr. 虽然考查结果对不同力场的敏感度是重要的, 我推荐现在使用PARSE.

注意 你可以使用PDB2PQR中的PROPKA来定义滴定状态. 但是上面的步骤不要这么做, 因为我们需要为我们的计算设定精确的滴定状态.

为进行内禀pKa的静电计算, 我们将需要孤立的氨基酸残基. 使用你喜欢的文本编辑器由2LZT-GLU35.pqr和2LZT-GLH35.pqr生成GLU 35或GLH 35残基格式. 将结果分别以GLU35.pqr和GLH35.pqr保存.

最后, 我们也需要对具有不带电荷残基的HEWL进行静电计算. 使用你喜欢的文本编辑器将2LZT-GLU35.pqr和2LZT-GLH35.pqr中的电荷设为0, 生成2LZT-noGLU35.pqr和2LZT-noGLH35.pqr. 这可以通过将PQR文件中倒数第二行设为0来实现, 例如:

ATOM    534  N   GLU    35       6.456  16.408  22.487 -0.5163 1.8240
ATOM    535  CA  GLU    35       6.354  15.205  23.349  0.0397 1.9080
ATOM    536  C   GLU    35       6.889  13.941  22.695  0.5366 1.9080
ATOM    537  O   GLU    35       7.705  13.192  23.277 -0.5819 1.6612
ATOM    538  CB  GLU    35       4.906  14.973  23.796  0.0560 1.9080
ATOM    539  CG  GLU    35       4.476  15.932  24.948  0.0136 1.9080
ATOM    540  CD  GLU    35       5.171  15.736  26.255  0.8054 1.9080
ATOM    541  OE1 GLU    35       5.844  14.786  26.570 -0.8188 1.6612
ATOM    542  OE2 GLU    35       5.038  16.682  27.056 -0.8188 1.6612
ATOM    543  H   GLU    35       5.671  16.799  22.056  0.2936 0.6000
ATOM    544  HA  GLU    35       6.856  15.382  24.215  0.1105 1.3870
ATOM    545  HB2 GLU    35       4.318  15.158  23.042 -0.0173 1.4870
ATOM    546  HB3 GLU    35       4.832  14.066  24.142 -0.0173 1.4870
ATOM    547  HG2 GLU    35       4.654  16.857  24.629 -0.0425 1.4870
ATOM    548  HG3 GLU    35       3.500  15.796  25.084 -0.0425 1.4870

可能变成

ATOM    534  N   GLU    35       6.456  16.408  22.487  0.0000 1.8240
ATOM    535  CA  GLU    35       6.354  15.205  23.349  0.0000 1.9080
ATOM    536  C   GLU    35       6.889  13.941  22.695  0.0000 1.9080
ATOM    537  O   GLU    35       7.705  13.192  23.277  0.0000 1.6612
ATOM    538  CB  GLU    35       4.906  14.973  23.796  0.0000 1.9080
ATOM    539  CG  GLU    35       4.476  15.932  24.948  0.0000 1.9080
ATOM    540  CD  GLU    35       5.171  15.736  26.255  0.0000 1.9080
ATOM    541  OE1 GLU    35       5.844  14.786  26.570  0.0000 1.6612
ATOM    542  OE2 GLU    35       5.038  16.682  27.056  0.0000 1.6612
ATOM    543  H   GLU    35       5.671  16.799  22.056  0.0000 0.6000
ATOM    544  HA  GLU    35       6.856  15.382  24.215  0.0000 1.3870
ATOM    545  HB2 GLU    35       4.318  15.158  23.042  0.0000 1.4870
ATOM    546  HB3 GLU    35       4.832  14.066  24.142  0.0000 1.4870
ATOM    547  HG2 GLU    35       4.654  16.857  24.629  0.0000 1.4870
ATOM    548  HG3 GLU    35       3.500  15.796  25.084  0.0000 1.4870

7.3.4 启动总静电能计算

我们将使用focusing来计算体系的静电势能和自由能.

提示 下面, 我们将计算 总静电自由能 – 比如, 包括自身电荷相互作用项的能量. 在接下来的步骤里计算溶剂化或迁移自由能时, 我们将去掉这些自身相互作用项. 因此, 在每个计算中要使用相同的格点参数(格点中心, 大小, 空间分布等), 这是非常重要的.

下面是我们计算每个溶剂化能使用的输入文件模板:

关于此输入文件, 许多方面需要注意:

• 一般地, 每个计算的compound.pqr将会改变, 但ref.pqr则不会. 选择一个分子作为ref.pqr(2LZT-GLU35.pqr是一个好的选择), 在所有计算中使用它.
• 我们使用的溶质介电常数($\ve_p$)是20(见pdie). 对pKa计算来说这个选择是常用的⁵ , 因为一般认为它暗含了溶质的内部松弛度和重排⁶.
• 对于分子表面(srfm smol), 我们使用了一个合理的高表面离散点密度(sdens 40.0). pKa和其它静电结果对表面选取有时是非常敏感的.

现在你有了足够的信息来计算相关分子的总静电能量: 2LZT-GLU35.pqr, 2LZT-GLH35.pqr, 2LZT-noGLU35.pqr, 2LZT-noGLH35.pqr, GLU35.pqr, GLH35.pqr. 通过修改上面的模板, 你应该能够为这些体系分别构建APBS输入文件. 当这些输入文件构建好后, 你可通过以下命令运行PB计算:

apbs foo.in | tee foo.out

其中foo.in是输入文件, 输出文件保存为foo.out.

7.3.5 启动迁移自由能计算

我们先前讨论过迁移自由能可以用两种方式来衡量. 由你自己决定用哪种方法; 对两种方法结果进行比较可得到足够好的格点设置. 正如前面提到的, 直接从总静电能中减除的方法通常是最稳定, 在这种方法中所有的计算采用一致的格点和溶质构象.

两种迁移自由能计算方法获得结果的不同, 通常都是由于计算中缺乏收敛性导致, 这可由降低格点间距解决(比如, 增加格点数目).

如果你选择将迁移自由能分解为溶剂化和库仑能差值, 除了前面章节列出的APBS计算外, 你还需要进行另外两项静电计算:

• 首先, 你需要在均匀电介质 $\ve_s=\ve_p$ 重新运行所有的APBS计算来得到溶剂化能. 这可通过修改前面章节中的输入文件来完成.
• 然后, 你需要计算库仑相互作用能. APBS的coulomb程序可衡量真空中一组电荷的库仑静电能. 该程序的用法是coulomb foo.pqr, 其中foo.pqr是你关注的PQR文件. 注意这个程序中有许多扩展选择. 不要忘记调整 $\ve_p$!

7.3.6 把所有的放到一起

这时, 你准备好了计算内禀pKa需要的所有东西. 考虑到你又可能出现故障, 这里我提供了许多有帮助的例子:

• 上面提到的PQR文件

  GLU35.pqr, GLH35.pqr, 2LZT-GLH35.pqr, 2LZT-GLU35.pqr, 2LZT-noGLH35.pqr, 2LZT-noGLU35.pqr

• 直接使用总静电能来计算GLH的迁移自由能需要的APBS输入文件

  2LZT-noGLH35.in, 2LZT-GLH35.in, GLH35.in

• 使用极性溶剂化能来计算GLH迁移自由能需要的APBS输入文件.

  2LZT-noGLH35-vac.in, 2LZT-GLH35-vac.in, GLH35-vac.in

• 直接使用总静电能来计算GLU的迁移自由能需要的APBS 输入文件.

  2LZT-noGLU35.in, 2LZT-GLU35.in, GLU35.in

• 使用极性溶剂化能来计算GLH迁移自由能需要的APBS输入文件.

  2LZT-noGLU35-vac.in, 2LZT-GLU35-vac.in, GLU35-vac.in

• 运行上面列出的所有APBS输入文件的Bash脚本. 假定apbs程序在你的PATH环境变量下.

  run-apbs.sh

• 用溶剂能来衡量迁移自由能时, 运行库仑能量计算的Bash脚本. 假定APBScoulomb程序在你的PATH环境变量下.

  run-coul.sh

7.3.7 接下来是什么?

通过我们简单的介绍, 你应该能试着衡量HIS 15和ASP 66的内禀pKa了. 你得到的结果与实验结果一致吗? 这些残基有什么不同?

到现在为止, 我们仅考察了内禀pKa, 并且忽略了可滴定基团之间的相互影响. Jens Nielsen开发了一个非常好的软件包pKaTool, 你可以用它来探究可滴定位点之间的耦合作用, 还有这些耦合作用对蛋白质体系滴定事件的影响. 他提供了一个教程, 可用来探究耦合滴定状态和熟悉pKaTool的使用.

• Bashford D, Karplus M. pKa's of ionizable groups in proteins: Atomic detail from a continuum electrostatic model. Biochemistry. 29 (44), 10219-25, 1990.
• Antosiewicz J, McCammon JA, Gilson MK. The determinants of pKas in proteins. Biochemistry. 35 (24), 7819-33, 1996.
• Nielsen JE, Vriend G. Optimizing the hydrogen-bond network in Poisson-Boltzmann 方程-based pKa calculations. Proteins-Structure Function and Genetics. 43 (4), 403-12, 2001.

8. 我的计算需要的内存太大!

APBS每个格点需要大约200 B的内存. 内存用量在进行计算之前就可预测, 数据是通过APBS提供的Python脚本psize.py获得的.

如果你的内存不足以满足计算的需要, 你还有其它选择:

• APBS计算可在多个机器上并行运算(共用分散内存!). 这项功能是由关键词mg-para提供的, 下面我们将详细说明, 读者也可参阅APBS用户手册.
• APBS计算可分解成一系列小的异步时序的运算, 每个运算需要的内存会小一些. 这项功能是由关键词mg-para async提供的, 下面我们将详细说明, 读者也可参阅APBS用户手册.
• 通过Gemstone将你的计算任务提交至外部计算资源.

8.1 并行计算: 示例

APBS源程序提供的肌动蛋白二聚体的例子(examples/actin-dimer/complex.pqr)是一个很大的体系, 也是并行focusing计算的极好例子.

我们将使用8个处理器并行计算来获得该复合物的静电势能图. 每个处理器在一个97³网格上使用并行focusing方法(见Baker et al, PNAS, 2001)来解决整个问题的一部分, 相邻处理器网格间有20%的重叠. 进行计算需要的输入文件应如下所示:

其中pdime 2 2 2定义了8-处理器的数组尺寸, ofrac 0.1定义了处理器计算之间有20%的重叠, dime 97 97 97定义了每个处理器计算量的大小. write pot dx pot指导APBS输出OpenDX格式的势能图, 输出文件为8个pot#.dx文件, 其中#指具体处理器的编号.

使用MPI版本的APBS来运行这个输入文件, 8个并行计算中每个运算都会得到问题域(fglen)不同位置的相当好的解. 注意8个OpenDX文件是分别由8个处理器写成的. OpenDX文件单独写成避免了并行计算时的通信问题, 并且单个文件相对来说是比较小的. 另外, 如果读者对问题域的特定部分感兴趣, 仅需少数文件便可获得局部势能信息.

然而, 大部分读者更关注整体势能. 许多程序(OpenDX, DataTank)可读入分开的势能文件并且生成整体势能图. 对于大多数其它程序, 需要读者事先得到重新组成的整体势能图; 为此APBS提供了mergedx程序. mergedx可将由并行计算得到的多个OpenDX文件组合成一张图. 这张图可从源分辨率数据中采样得到较粗糙的数据组, 以实现粗略而快速的观察等. 例如, 以下命令

mergedx 65 65 65 pot0.dx pot1.dx pot2.dx pot3.dx pot4.dx pot5.dx pot6.dx pot7.dx

将会生成gridmerged.dx文件. 这个文件是从8个OpenDX文件中采集较粗糙的数据组生成的65³文件, 它比较适合于粗略观察. 下面是mergedx输出结果的一个例子 (方法见3.1.4.1):

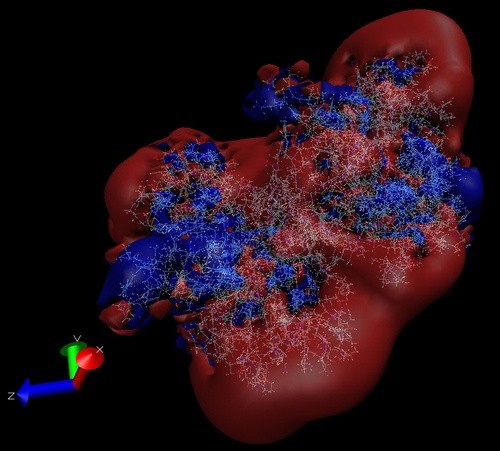
图 8.1. 并行计算得到的肌动蛋白二聚体等势面

注意采样不是必须的, 并且对高质量的观察和定量分析是不适用的.

8.2 异步时序计算

对于不能进行并行计算的程序, 也可通过MPI实现上面章节描述的步骤. 特别地, 你可以增加

async n

至APBS输入文件的ELEC mg-para, 使得单处理器模拟进行n个并行计算中的任务之一.

APBS异步时序运算得到的标量图可由上面提到的mergedx程序整合到一块. 目前, 对于APBS异步时序运算得到的能量和力, 需要手动将单个计算得到的文件合并起来. 这可由简单的shell脚本实现.

作为具体的例子, 我们可以修改上面的输入文件. 在ELEC状态中加入async 0命令, 这使得APBS运行并行计算中的第一个处理器. 修改后的输入文件应该如下:

这将生成一个名为pot.dx的OpenDX-格式势能图, 它对应于并行计算中处理器0的输出结果. 使用async 1, async 2, ..., async 7运行其它的APBS计算将相应地产生剩余处理器的OpenDX图. 如上面所述, 使用mergedx可将这些图整合到一块.

9. 怎样将APBS用于我的分子动力学软件(计算MM/PBSA, 等)?

Robert Konecny(McCammon group)开发的iAPBS软件包提供了APBS与AMBER, NAMD和CHARMM的C/C++/FORTRAN对接. 更多详细的信息可见iAPBS主页.

APBS也与正在开发的TINKER软件包新版本进行了对接. 具有APBS支持的TINKER很快可以从http://dasher.wustl.edu/tinker/得到.

10. 怎样通过网络运行APBS?(Gemstone)

通过Gemstone服务, 你可以在网上运行APBS. 本章节将展示Gemstone怎样通过命令行对接进行大多数的APBS计算. 更方便的一点是, 你能使用NBCR的资源来代替自己的!

10.1 获取Gemstone

在开始之前, 你需要为Firefox网页浏览器下载并安装Gemstone扩展, 可从http://gemstone.mozdev.org获得.

10.2 使用PDB2PQR准备结构

我们将从使用PDB2PQR准备结构开始. 首先, 你需要从Protein Data Bank下载PDB文件. 在这个例子中, 我们使用1FAS.

从Firefox菜单打开Gemstone对接Tools→Gemstone. 在Gemstone屏幕右边的Gemstone菜单中选择应用PDB2PQR: Utils→PDB2PQR. 选择你刚下载的PDB文件以及你关注的其它关于PDB2PQR的选择. 这时, 屏幕应如下所示:

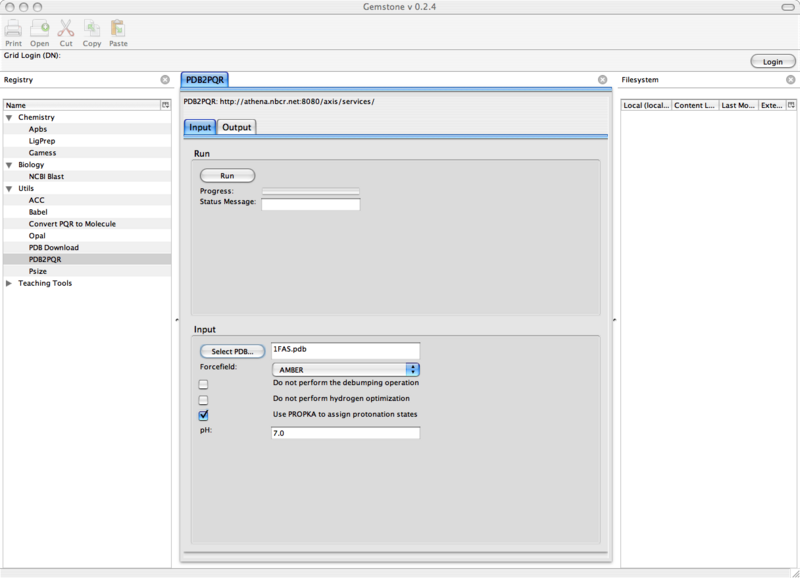
图 10.1. Gemstone PDB2PQR计算

到前面Run Gemstone计算, 检查stdOut和stdErr获取任何提示信息, 下载生成的PQR文件.

10.3 使用APBS进行静电计算

现在我们准备好了通过Gemstone进行1FAS静电势能的APBS计算. 打开Gemstone屏幕右边的Chemistry→Apbs菜单. 下面的章节我们将逐个讲解中间部分的输入标签.

10.3.1 Calculation

移至中间部分的Calculation标签.

大部分Mathematics设置可不需更改；当然, 你也可以试着修改离散化和表面定义来看一下对你的结果有何影响.

在Molecules下, 载入上面章节中准备好的1FAS PQR文件.

本次计算中, 在Energy and Force下不要选择任何选项.

这时, 你的屏幕应如下所示:

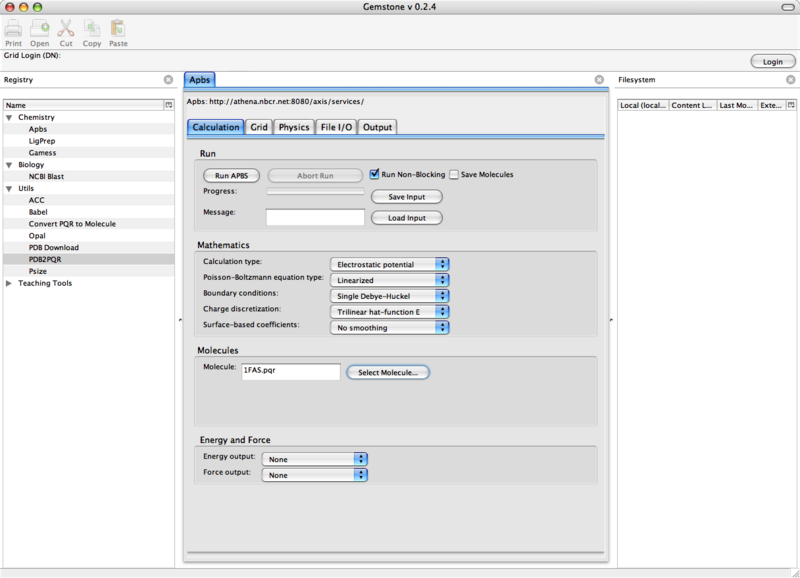
图 10.2. Gemstone APBS/Calculation窗口

10.3.2 Grid

下面, 移至中间部分的Grid标签.

在General下, 设置X, Y和Z的Grid points值为97.

在Coarse Grid下, X, Y和Z的Lengths都设为100. 选中Center Grid on molecule.

在Fine Grid下, X, Y和Z的Lengths都设为80. 选中Center Grid on molecule.

在此次计算中不用管Parallel Execution.

这时, 你的屏幕应如下所示:

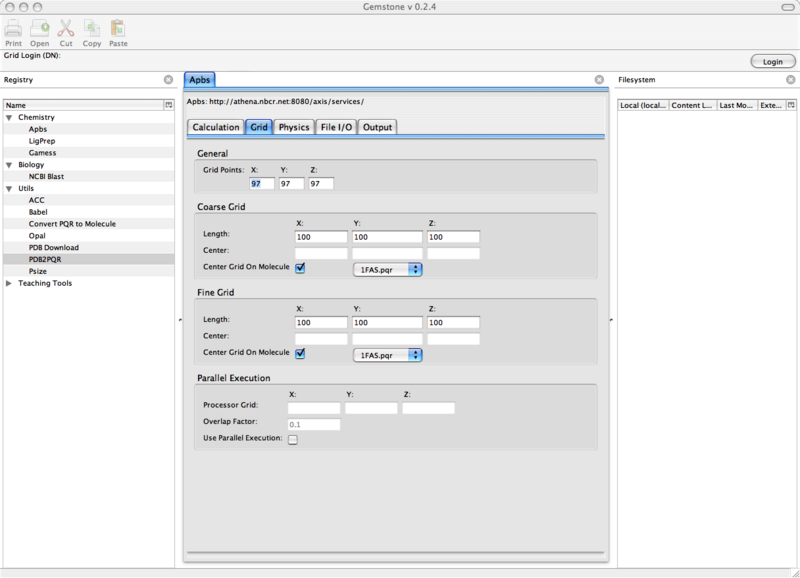
图 10.3. Gemstone APBS/Grid窗口

10.3.3 Physics

下面, 移至中间部分的Physics标签.

选择任何你喜欢的值, 默认值对大多数可视化计算来说是可行的.

这时, 你的屏幕应如下图:

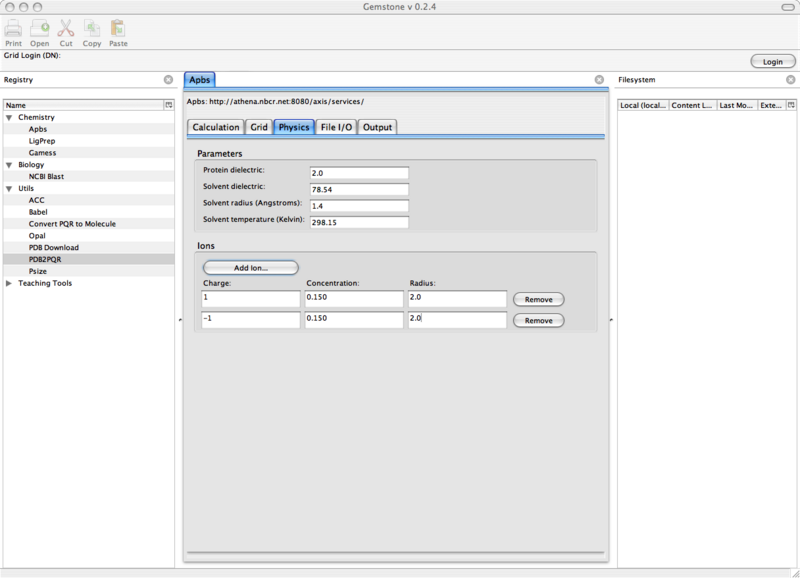
图 10.4. Gemstone APBS/Physics窗口

10.3.4 File I/O

下面, 移至中间部分的File I/O标签.

你可以不必改这些设置, 除非你想观察其它的性质.

这时, 你的屏幕应如下所示:

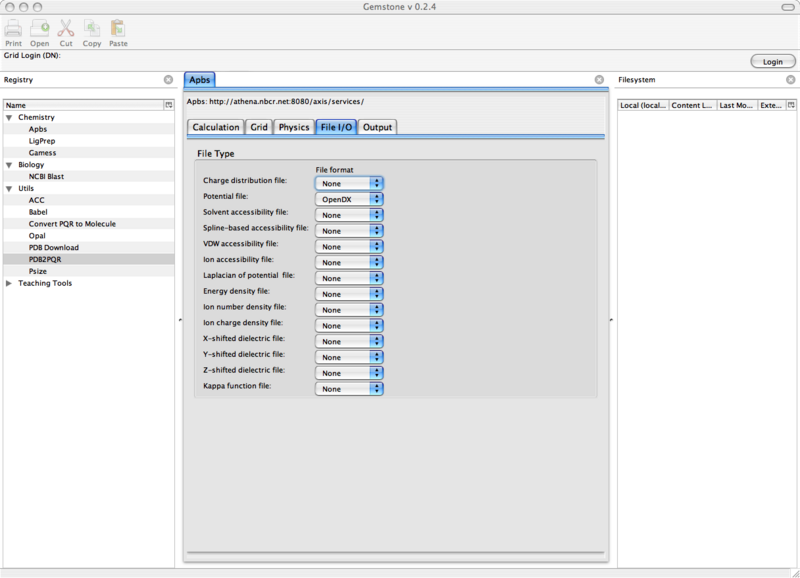
图 10.5. Gemstone APBS/File I/O窗口

10.3.5 运行计算

最后, 返回到Calculation标签下, 选择Run APBS. 一会儿后, 结果将出现在中间部分的输出标签下. 计算结束时, 你将看到:

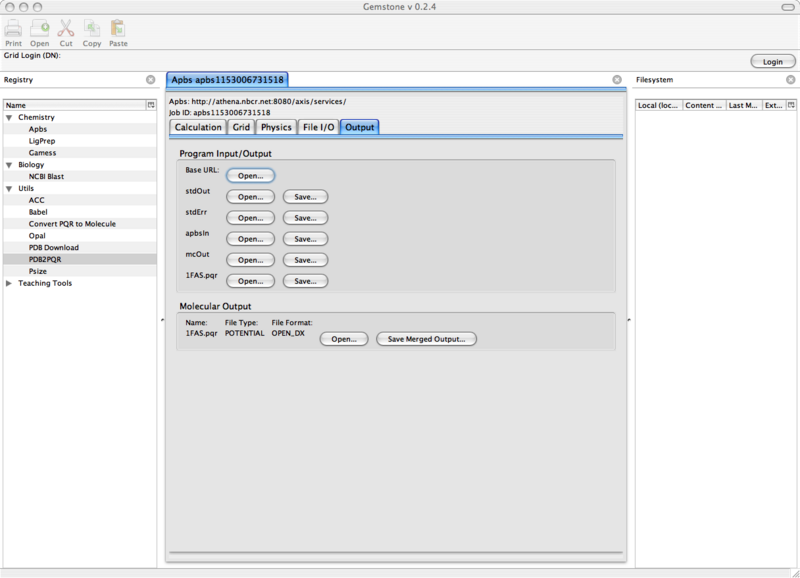
图 10.6. Gemstone APBS/Calculation窗口(计算结束)

特别地, 你可以选择是否保存计算得到的势能文件.

10.3.6 其它计算

几乎所有本教程中的例子都可以通过Gemstone进行. 更进一步, 可以上传输入文件 并使用Gemstone作为进入其它研究机构网络服务的入口.

11. 更多例子...

除了这里介绍的相对简单的应用之外, APBS软件包中含有大量其它的例子, 包括电离能, 蛋白质之间相互作用, 并行计算等.

12. 所有这些都没有回答我的问题...

请访问APBS用户邮件列表. 当你找到问题的答案后, 请将它贴到邮件列表中.