对于某些具有共性的问题, 数学和物理在处理时常会使用不同的术语和说辞. 一般而言, 数学上的说辞更通用抽象, 而物理上的则更具体形象直观. 在学习某种理论时, 如果能将这两个领域的知识结合起来, 从抽象到具体, 从具体到抽象, 互相映射, 可以加深理解, 培养直觉. 从现今的科技文献上来看, 不同领域之间的相互借鉴大量存在, 但术语说辞方面的分裂趋势却愈甚. 这种趋势一方面源于语言分化的本性, 另一个方面也反应了不同领域对话语权的争夺. 但这种分裂会人为地在不同学科之间建立藩篱, 增加隔阂, 加厚了新人进入的壁垒, 不利于科学共同体的发展. 以目前大火的人工智能, 机器学习领域而言, 其基础概念大多源于数学, 物理, 统计, 却往往会换成新的名称, 弄一些噱头唬人: 数组不叫数组, 叫张量, 期望不叫期望, 叫注意力, 大有靠向量化投资黑话的趋势.
物理中的主轴分析与数学中的主成分分析, 就是这种术语说辞不同的例子. 这两套语言实际处理的问题是一样的, 采用的方法也类似, 理解了之后, 会发现它们实际上是一回事:
物理中的惯性张量, 数学中的协方差矩阵, 二者只差一个常数单位矩阵, 其本征值(主转动惯量/主成分贡献)差同样的常数, 其本征值(主轴/主成分)相同.
遗憾的是, 很少有人将它们放在一起说, 都是各说各话, 只讲自己熟悉的一套术语. 我是从物理知晓主轴分析的, 物理的说辞我知道得早, 也容易建立直观的认识. 等学习了数学中协方差, 协方差矩阵, 协方差分析, 主成分分析之类的说辞后, 隐约觉得就是物理上的主轴分析, 也确实看到有人这么称呼. 这里我就从原始公式出发, 看看两套说辞是如何统一起来的.
物理学中, 惯性张量为二阶张量(即矩阵, 所以可称为惯性矩阵), 定义为:
$$ \mathbf{I} = \begin{bmatrix} I{xx} & I{xy} & I{xz} \ I{yx} & I{yy} & I{yz} \ I{zx} & I{zy} & I_{zz} \end{bmatrix} $$
矩阵的三个对角元称为转动惯量, 表征了在x, y, z三个轴上转动惯性的大小,
$$ I{xx}\ \stackrel{\mathrm{def}}{=}\ \int\ (y^2+z^2)\ \mathrm{d}m \ I{yy}\ \stackrel{\mathrm{def}}{=}\ \int\ (x^2+z^2)\ \mathrm{d}m \ I_{zz}\ \stackrel{\mathrm{def}}{=}\ \int\ (x^2+y^2)\ \mathrm{d}m $$
非对角元称为惯性积, 具有对称性,
$$ I{xy}=I{yx}\ \stackrel{\mathrm{def}}{=}\ - \int\ xy\ \mathrm{d}m \ I{xz}=I{zx}\ \stackrel{\mathrm{def}}{=}\ - \int\ xz\ \mathrm{d}m \ I{yz}=I{zy}\ \stackrel{\mathrm{def}}{=}\ - \int\ yz\ \mathrm{d}m $$
如果考虑离散的质点系, 则上面方程中的积分化为累加求和, 整个惯性矩阵为
$$ \mathbf{I} = \begin{bmatrix} \Sum_{i=1}^N m_i(y_i^2+zi^2) & -\sum{i=1}^N m_i x_i yi & -\sum{i=1}^N m_i x_i zi \ .. & \sum{i=1}^N m_i(x_i^2+zi^2) & -\sum{i=1}^N m_i y_i zi \ .. & .. & \sum{i=1}^N m_i(x_i^2+y_i^2) \end{bmatrix} $$
这是一个三阶实对称矩阵, 可以对其进行对角化, 所得的三个本征值称为主转动惯量(不混淆的情况下也简称主轴), 对应的三个本征向量为惯性主轴(简称主轴). 三个主轴相互垂直, 以其作为新坐标系的三个轴, 就得到了主轴坐标系. 使用主轴坐标系描述物体的转动更简单, 因为不同主轴之间的耦合最小. 因而, 惯性主轴方向上质量的分布具有某种极值性.
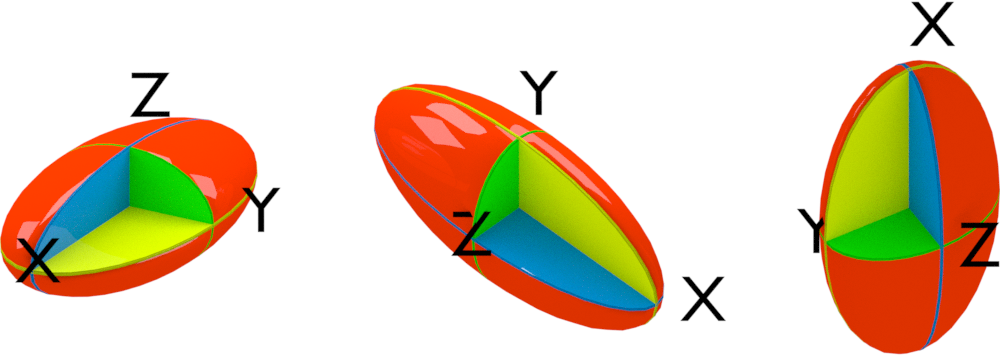
上面就是物理中的主轴分析. 物理中还常会使用惯性椭球来表示主轴分析的结果, 使人更易获得直观印象. 将三个主转动惯量从小到大排列, $I_a$, $I_b$, $I_c$, 以其平方根的倒数作为椭球的三个半轴长度, 就得到了所谓的惯性椭球
$$ I_a x² + I_b y²+I_c z² =1 \ {x²/1/I_a} + {y²/1/I_b} +{z²/1/I_c} =1 $$
此外, 可以根据三个主转动惯量的大小关系对物体进行分类. 之所以对物体作这些区分, 是因为在处理转动时有一定的区别.
化学中则借用了这种做法对分子的对称性进行分类
线型对应的物理体就是线段. 线型分子很常见, 同核或异核的双原子分子皆属此类, 如H₂, CO等. 有些三原子分子也属此类, 如CO₂.
球陀螺也就是球体, 为平面圆绕其直径旋转所成的旋转体. 这种分子的对称性比较高, 常见于Td, Ih等点群的分子, 如CH₄, C₆₀等.
不对称陀螺为三个主轴不等的椭球体, 不属于旋转体, 无法由某个平面图形绕轴旋转形成. 各种形状不规则的物体大致都属于此类. 这种分子一般没有什么对称性.

最后两种陀螺都是平面椭圆的旋转体, 区别在于长陀螺的旋转轴为短轴, 扁陀螺的旋转轴为其长轴. 这两类陀螺都有一个特征轴和两个简并轴. 若特征轴转动惯量小于简并轴, 则为长陀螺. 常见物体中的橄榄球属于此类. 化学中的扁长分子大致是细长的, 如短的直链烃类, C₂H₂, C₂H₄.
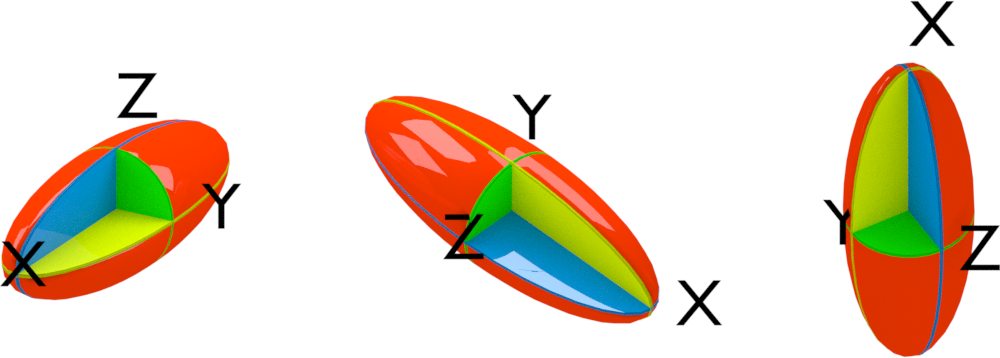
若特征轴转动惯量大于简并轴, 则为扁陀螺, 如常见的飞盘或某些药片. 扁圆分子大致是平面类的, 如苯.
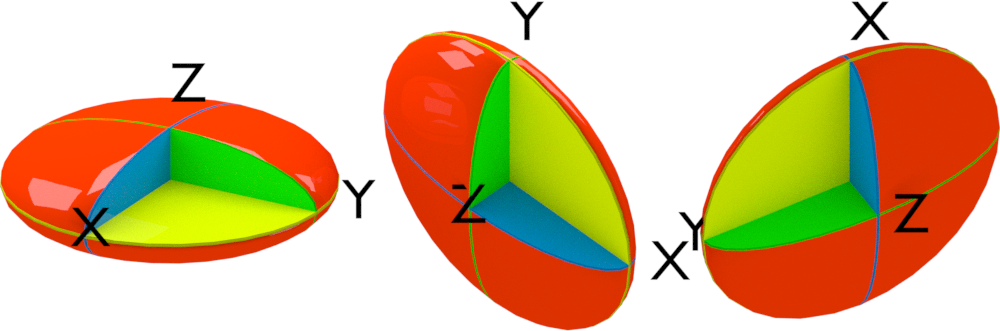
数学统计和机器学习领域中, 处理点集时, 常会用主成分分析, 获得点集在不同维度上的分布情况, 以便进行后续的降维处理.
以三维为例: 给定三维空间中的$N$个点, 其中每个点具有权重$w_i$, 坐标$x_i$, $y_i$, $z_i$, 求其三个主成分.
先对点集进行预处理, 使其加权中心为零. 这相当于进行平移操作, 方便后面的操作运算, 不会影响主成分分析的结果,
再计算协方差矩阵
$$ \mathbf{I} = \begin{bmatrix} C{xx} & C{xy} & C{xz} \ C{yx} & C{yy} & C{yz} \ C{zx} & C{zy} & C_{zz} \end{bmatrix} $$
所谓协方差, 是指两个变量对其均值(也称期望)偏离乘积的平均值. 如果两个变量相同, 协方差也就变为方差:
$$C_{αβ}= <(α-<α>) (β-<β>)>$$
应注意文献中对于均值, 平均值, 期望可能会使用不同的符号, 如$\bar x, <x>, E(x)$等.
整个协方差矩阵为
$$ \mathbf{C} = \begin{bmatrix} \Sum_{i=1}^N w_i xi^2/N & \Sum{i=1}^N w_i x_i yi/N & \Sum{i=1}^N w_i x_i zi/N \ .. & \Sum{i=1}^N w_i yi^2/N & \Sum{i=1}^N w_i y_i zi/N \ .. & .. & \Sum{i=1}^N w_i z_i^2/N \end{bmatrix} $$
最后对协方差矩阵进行对角化, 所得三个本征向量即为待求的主成分, 相应的本征值即为每个主成分的贡献. 一般会将本征值从大到小排列, 本征值越大, 贡献越大. 也常使用每个本征值对所有本征值加和的百分比表示.
从前面的公式和方法可以看出, 主成分分析与主轴分析很类似, 区别仅在于使用的是协方差矩阵而不是惯性矩阵. 那么就让我们来看看它们之间的联系.
物理中惯性矩阵的常用符号$I$, 与数学中单位矩阵的常用符号相同, 为避免混淆, 我们这里换用$T$来表示惯性矩阵.
如果我们将每个点的权重视为质量, 有
$$╤ T{xx}&=\Sum{i=1}^N m_i(y_i^2+zi^2) = \Sum{i=1}^N m_i(r_i^2-xi^2) \ &=\Sum{i=1}^N m_i ri^2-\Sum{i=1}^N m_i xi^2 \ &=\Sum{i=1}^N m_iri^2-NC{xx} \ T{xy}&=-\Sum{i=1}^N m_i x_i yi = -N C{xy} ╧$$
对比一下可以发现
$$╤ T&=RI-NC \ C&={R/N}I-{1/N}T ╧$$
其中 $R=\Sum_{i=1}^N m_i r_i^2$, $I$为单位矩阵.
若矩阵$P$可以对角化$T$,
$$ P^{-1}TP=Λ \ P^{-1}(RI-NC)P=P^{-1}RIP-P^{-1} NCP=RI-NP^{-1}CP=Λ \ P^{-1}CP={R/N}I-{1/N}Λ $$
可见, 这两个矩阵的本征向量是一致的, 本征值差了一个常数.
因此, 对角化惯性矩阵还是协方差矩阵, 本质上没有区别, 所得本征向量也不会改变. 主轴和主成分实际是一回事. 根据物理上的平行轴定理, 协方差矩阵所得的主轴相对于惯性矩阵所得的主轴进行了原点的平移.
主轴分析和主成分分析在报告结果时有个小区别, 主转动惯量常从小到大排列, 主成分贡献常从小到大排列. 根据前面的结论, 由于二者之间符号相反, 因而二者所用的顺序实际是一致的, 转动惯量越小的方向, 质量分布越集中, 主成分贡献越大. 相反, 转动惯量越大的方向, 质量分布越分散, 主成分贡献越小.
现实世界是三维的, 但数学上可以考虑多维空间. 多维空间存在多个坐标维度, 主轴分析的方法类似, 只不过矩阵变为 $N×N$ 的. 这种情况下, 我们称其为超主轴, 或高维主轴是没问题的.
如果各个维度上对应的并非实际坐标, 而是代表某些特征的任意值, 比如颜色, 价格, 购买率等, 主成分分析仍然适用. 这种情况下仍将所得的本征向量称为主轴就有点过于狭隘, 不合适了, 数学上称其为主成分可能更合适.
相应地, 为将对主成分本质的理解也从物理中脱离出来, 可以从优化角度切入: 主成分为原成分(原特征)的线性组合, 用以最大化地描述点集的特征分布. 大致而言, 是在某些约束条件下, 点集沿主成分分布最大化, 彼此间耦合最小化. 对应到主轴分析的语言, 就是求一个新的直角坐标系, 使得一组点在新坐标轴上的分布最大化.
优化表述是目前人工智能领域最流行的范式, 因为这样问题最终可以化归为网络的训练, 以便在已有框架内解决. 我不是很熟悉这套作法, 就不涉及了. 具体可参考 从优化的角度看PCA降维的原理.
主成分分析的降维作用, 从物理角度看, 类似于用第一主轴或前几个主轴来代表物体的大致形状. 若第一主轴远小于其他主轴, 那么物质大致集中于第一主轴方向, 可以将物体近似看做只沿第一主轴方向分布, 变为线型体系, 这样就将物体从三维降为一维.
以模拟轨迹的主成分分析为例. 轨迹中的每一帧结构都有很多特征参数, 简单的如能量, 压力, 结构参数, 复杂点的如RMSD. 每个特征参数可以视为一个维度, 对感兴趣的维度进行主成分分析, 所得的主成分就是原特征参数的线性组合, 并不再具有明确的物理意义, 但依然可以据其对轨迹结构进行聚类, 或者将其用于绘制自由能形貌图. 由于主成分具有分布集中的特点, 使用主成分描述可以减少原特征参数之间的耦合, 使得聚类效果更好, 形貌图特征更明显.
进行主成分分析时使用矩阵的特征值分解, 是因为所处理的是实对称矩阵. 对于实对称矩阵, 奇异值分解与特征值分解是一致的. 但如果处理的并非实对称矩阵, 那就只能使用奇异值分解. 但这两种分解方法都只适用于处理矩阵, 也就是二维张量, 并借以对其进行降维. 对于更高阶的张量, 也有对应的分解方法. 具体的, 就不是本文能覆盖的了.
两个实对称矩阵相差一个常数单位矩阵时, 其本征向量不变, 其本征值相差同样的常数.这是一种很特殊的情况. 更一般情况下, 如果二者相差的对角矩阵并非常数, 它们之间的本征值之间也存在一定的关系, 相关讨论可参考Eigenvalues of Symmetric Matrix Plus Diagonal Matrix