- 2016-06-24 10:28:49
- 2024-01-20 15:57:33: 优化图片另存设置
经常有人询问怎么计算分子的尺寸大小. 对这个问题, 首先要明确所谓分子的大小, 并不是一个确定的物理量, 而是基于某些模型下的一些经验值. 根据不同的假定, 得到的分子大小也不同. 因此, 你可能发现, 对同一分子, 并没有统一的大小数据, 不同人所引用的尺寸数据可能差距很大. 更多讨论可参考Sobereva的博文谈谈分子半径的计算和分子形状的描述.
作为最简单的模型, 我们可以将分子中的原子视为固定半径的圆球, 分子由这些圆球堆积而成. 在这种模型下, 容易定义分子的尺寸大小, 就是分子在三个垂直方向上的最小长度. 如果将分子完全放在一个长方体盒子中, 这样的盒子是最小的.
在计算时, 我们首先需要指定每个原子的半径. 由于原子半径同样不是一个确定的物理量, 所以有多种定义方式, 如共价半径, 范德华半径, 离子半径, 有效半径, 等等. 在计算分子大小时, 我们一般使用范德华半径. 对于它的数值, 最常用的一套数据是由Pauling开始, 经Bondi细化, Gavezotti, Rowland和Taylor等人修正给出的, 但并没有包含所有的主族元素. Mantina等人根据这套数据, 利用量化方法得到了包含所有主族元素的一套自洽的半径数据, 见论文: Manjeera Mantina, Adam C. Chamberlin, Rosendo Valero, Christopher J. Cramer, Donald G. Truhlar; Consistent van der Waals Radii for the Whole Main Group; J. Phys. Chem. A 113(19):5806-5812, 2009; 10.1021/jp8111556. 对某些金属元素, 这套半径的某些数值可能不够准确, 使用时请注意核查. 胡盛志等人在论文胡盛志, 谢兆雄, 周朝晖; 晶体范德华半径的70年; 物理化学学报, 26(7): 1795-1800, 2010中总结了一套更全的半径, 几乎包含了周期表中所有的元素. 对一些常用元素, 这套半径与Bondi的相差不大. 具体使用时, 可根据情况选择. 下面是两套半径的对比
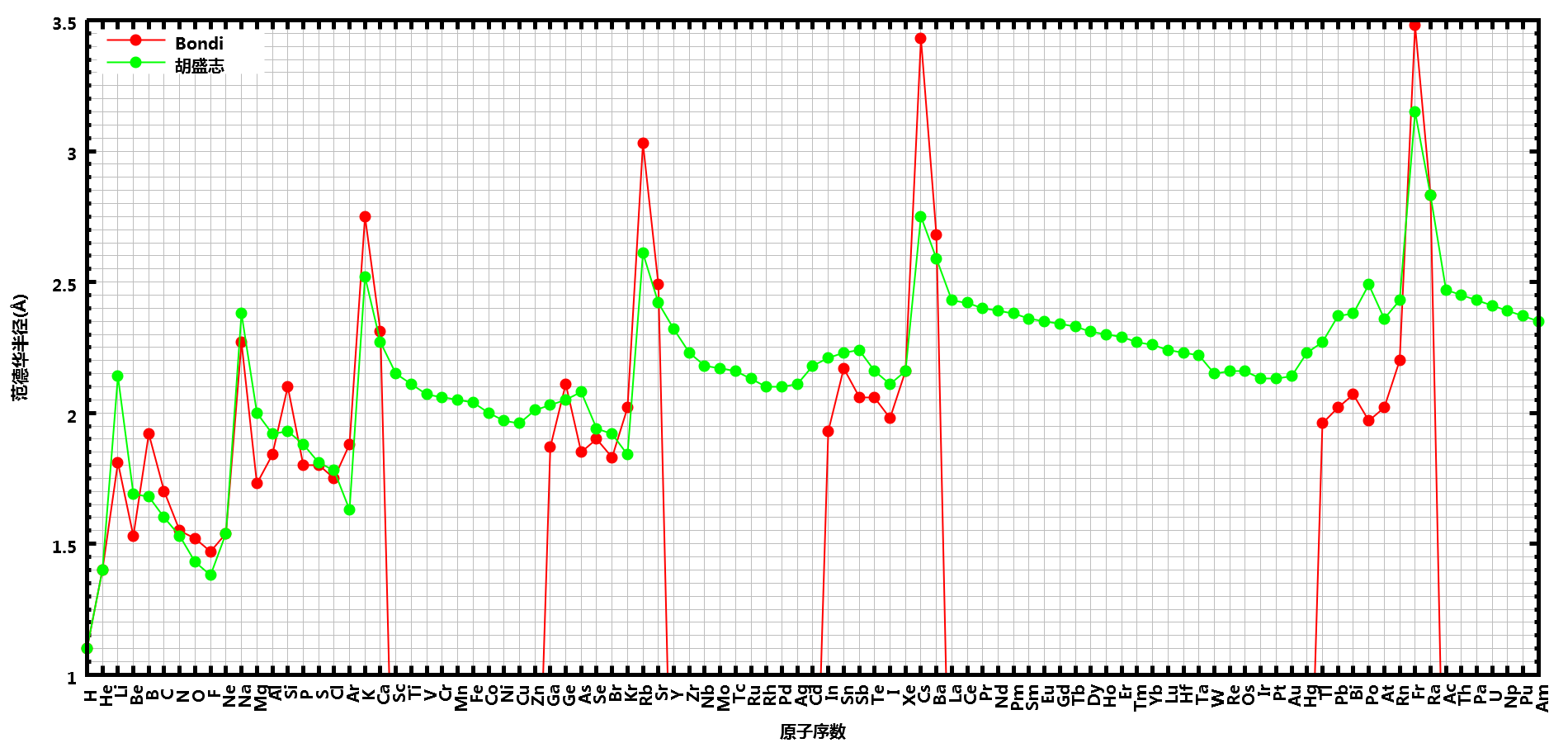
确定了使用的范德华半径之后, 下面就要确定计算分子大小时采用的三个垂直方向. 考虑到分子的旋转, 我们可以取分子的三个惯性主轴作为确定分子大小的方向. 所有原子在某一主轴上投影的最大距离, 就可以作为分子在这个主轴方向上的长度.
明确了半径和方向, 就容易计算分子的大小了. 为方便计算, 我将这种算法作成了一个在线的小工具, 只要给定分子中原子的坐标, 指定采用的半径, 就可以方便地得到分子的尺寸. 如果你想对某些原子使用自定义的半径, 直接在元素 原子量(amu) 半径(Å)中修改相应的半径数值即可.
得到了三个方向的尺寸后, 可以根据某些规则取最值或是三个尺寸的平均值作为分子的直径.
<table style="width:100%">
<tr>
<td style="width:70%">元素 xyz坐标(Å)<br/><textarea id="xyz" style="width:100%; height:100px; resize: none"></textarea></td>
<td style="width:30%">元素 原子量(amu) 半径(Å)<br><textarea id="masrad" style="width:100%; height:100px; resize: none"></textarea></td>
</tr>
<tr>
<td colspan="2">原子范德华半径:
<input type="radio" name="rad" onclick="setRad(0)">Bondi
<input type="radio" name="rad" onclick="setRad(1)">胡盛志
<input type="button" value="计算" onclick="showBox()"></td>
</tr>
<tr>
<td colspan="2">
分子三维尺寸(Å): <span id='size'></span><br>
算术平均半径(Å): <span id='Ravg'></span><br>
几何平均半径(Å): <span id='Rgvg'></span><br>
距中心距离值(Å): <span id='Rmax'></span>
</td>
</tr>
<tr>
<td colspan="2">
<script>var Mol1=new ChemDoodle.TransformCanvas3D('Mol-1',500,400);
var labBox1, labBox2, labBox3, labBox4, labBox5, labBox6, labBox7, labBox8, labBox9, labBox10, labBox11, labBox12
Mol1.specs.backgroundColor = '#000';
Mol1.specs.text_color='#fff';
Mol1.specs.shapes_color = '#fff';
Mol1.specs.set3DRepresentation('van der Waals Spheres');Mol1.specs.projectionPerspective_3D = false;Mol1.specs.proteins_ribbonCartoonize = true;Mol1.loadContent('');function setProj1(yesPers){Mol1.specs.projectionPerspective_3D = yesPers;Mol1.setupScene();Mol1.repaint()}function setModel1(model){Mol1.specs.set3DRepresentation(model);Mol1.setupScene();Mol1.repaint()}
function setBg1(chk){Mol1.specs.backgroundColor=chk?"#fff":"#000"
Mol1.specs.shapes_color =chk?"#000":"#fff";
Mol1.setupScene();
Mol1.repaint()}
function refig() {
Mol1=new ChemDoodle.TransformCanvas3D('Mol-1',$('wid').value,$('hit').value);
setBg1($("bg").checked);
Mol1.specs.set3DRepresentation('van der Waals Spheres');
Mol1.specs.projectionPerspective_3D = false;
Mol1.specs.proteins_ribbonCartoonize = true;
showBox();
//Mol1.setupScene();Mol1.repaint()
}
</script><br>
<span class="meta">图片: 宽 <input type="input" style="width:4em" id='wid' value=400>
高 <input type="input" style="width:4em" id="hit" value=300>
<button onclick="refig()">重载</button>
<input type="checkbox" id="bg" onclick="setBg1(this.checked)">白底黑字<br>
标注: 边
<input type="checkbox" onclick="labBox1=this.checked;showBox();">1
<input type="checkbox" onclick="labBox2=this.checked;showBox();">2
<input type="checkbox" onclick="labBox3=this.checked;showBox();">3
<input type="checkbox" onclick="labBox4=this.checked;showBox();">4
<input type="checkbox" onclick="labBox5=this.checked;showBox();">5
<input type="checkbox" onclick="labBox6=this.checked;showBox();">6
<input type="checkbox" onclick="labBox7=this.checked;showBox();">7
<input type="checkbox" onclick="labBox8=this.checked;showBox();">8
<input type="checkbox" onclick="labBox9=this.checked;showBox();">9
<input type="checkbox" onclick="labBox10=this.checked;showBox();">10
<input type="checkbox" onclick="labBox11=this.checked;showBox();">11
<input type="checkbox" onclick="labBox12=this.checked;showBox();">12<br>
视图: <input type="radio" name="group2" onclick="setProj1(true)">投影<input type="radio" name="group2" onclick="setProj1(false)" checked="">正交<br>
模型: <input type="radio" name="model" onclick="setModel1('van der Waals Spheres')">范德华球<input type="radio" name="model" onclick="setModel1('Stick')">棍状<input type="radio" name="model" onclick="setModel1('Wireframe')">线框<input type="radio" name="model" onclick="setModel1('Line')">线型<input type="checkbox" onclick="Mol1.specs.atoms_displayLabels_3D=this.checked;Mol1.repaint()">名称<br>左键: 转动 滚轮: 缩放 双击: 开关自动旋转 Alt+左键: 移动</span>
</td>
</tr>
</table><script>
var $=function(id){return document.getElementById(id)}
$('xyz').value=
'O 0.0000 0.0000 0.1173\n'
+'H 0.0000 0.7572 -0.4692\n'
+'H 0.0000 -0.7572 -0.4692\n'
function showBox() {
var i, j, tmp, Iabc=[], Mass=[], Radi=[], Satm=[], Xatm=[], Yatm=[], Zatm=[]
var xyz=$('masrad').value.replace(/^\s*\n*/,"").replace(/\s*\n*$/,"").replace(/\s+[\n|$]/g,"\n").split('\n')
for(i=0; i<xyz.length; i++) {
tmp=xyz[i].split(/\s+/)
Mass[tmp[0]]=parseFloat(tmp[1])
Radi[tmp[0]]=parseFloat(tmp[2])
ChemDoodle.ELEMENT[tmp[0]].covalentRadius=parseFloat(tmp[2])
ChemDoodle.ELEMENT[tmp[0]].vdWRadius=parseFloat(tmp[2])
}
var xyz=$('xyz').value.replace(/^\s*\n*/,"").replace(/\s*\n*$/,"").replace(/\s+[\n|$]/g,"\n").split('\n')
var Natm=xyz.length, Xcom=0, Ycom=0, Zcom=0, Wgt=0
for(i=0; i<Natm; i++) {
tmp=xyz[i].split(/\s+/)
tmp[0]=tmp[0].replace(/\d+/,"")
Satm[i]=tmp[0]; Wgt += Mass[tmp[0]]
Xatm[i]=parseFloat(tmp[1]); Xcom += Mass[tmp[0]]*parseFloat(tmp[1])
Yatm[i]=parseFloat(tmp[2]); Ycom += Mass[tmp[0]]*parseFloat(tmp[2])
Zatm[i]=parseFloat(tmp[3]); Zcom += Mass[tmp[0]]*parseFloat(tmp[3])
}
Xcom /= Wgt; Ycom /= Wgt; Zcom /= Wgt
for(i=0; i<Natm; i++) { Xatm[i] -= Xcom; Yatm[i] -= Ycom; Zatm[i] -= Zcom }
var Ixyz=[ [0,0,0], [0,0,0], [0,0,0] ]
for(i=0; i<Natm; i++) {
tmp= Mass[Satm[i]]
Ixyz[1-1][1-1] += tmp*(Yatm[i]*Yatm[i]+Zatm[i]*Zatm[i])
Ixyz[2-1][2-1] += tmp*(Zatm[i]*Zatm[i]+Xatm[i]*Xatm[i])
Ixyz[3-1][3-1] += tmp*(Xatm[i]*Xatm[i]+Yatm[i]*Yatm[i])
Ixyz[1-1][2-1] -= tmp*Xatm[i]*Yatm[i]
Ixyz[1-1][3-1] -= tmp*Xatm[i]*Zatm[i]
Ixyz[2-1][3-1] -= tmp*Yatm[i]*Zatm[i]
}
Ixyz[2-1][1-1] = Ixyz[1-1][2-1]
Ixyz[3-1][1-1] = Ixyz[1-1][3-1]
Ixyz[3-1][2-1] = Ixyz[2-1][3-1]
var V=[], W=[]
Jacobi(Ixyz, V, W)
for(i=0; i<Natm; i++) {
var Vtmp = [ Xatm[i], Yatm[i], Zatm[i] ]
Xatm[i] = V[0][0]*Vtmp[0]+V[0][1]*Vtmp[1]+V[0][2]*Vtmp[2]
Yatm[i] = V[1][0]*Vtmp[0]+V[1][1]*Vtmp[1]+V[1][2]*Vtmp[2]
Zatm[i] = V[2][0]*Vtmp[0]+V[2][1]*Vtmp[1]+V[2][2]*Vtmp[2]
}
var maxRx=-1E10, maxRy=maxRx, maxRz=maxRx, maxR=maxRx,
minRx= 1E10, minRy=minRx, minRz=minRx, minR=minRx, avgR=0.
for(i=0; i<Natm; i++) {
maxRx=Math.max(maxRx, Xatm[i]+Radi[Satm[i]])
maxRy=Math.max(maxRy, Yatm[i]+Radi[Satm[i]])
maxRz=Math.max(maxRz, Zatm[i]+Radi[Satm[i]])
tmp=Math.sqrt(Xatm[i]*Xatm[i]+Yatm[i]*Yatm[i]+Zatm[i]*Zatm[i])+Radi[Satm[i]]
maxR =Math.max(maxR, tmp)
avgR += tmp
minRx=Math.min(minRx, Xatm[i]-Radi[Satm[i]])
minRy=Math.min(minRy, Yatm[i]-Radi[Satm[i]])
minRz=Math.min(minRz, Zatm[i]-Radi[Satm[i]])
minR =Math.min(minR, tmp)
}
Xbox=maxRx-minRx
Ybox=maxRy-minRy
Zbox=maxRz-minRz
avgR /= Natm
$('size').innerHTML=fmtNum(Xbox,8.3).trim()+'×'+fmtNum(Ybox,8.3).trim()+'×'+fmtNum(Zbox,8.3).trim()
$('Ravg').innerHTML=fmtNum((Xbox+Ybox+Zbox)/6, 8.3).trim()
$('Rgvg').innerHTML=fmtNum(Math.pow(Xbox*Ybox*Zbox, 1/3.)/2, 8.3).trim()
$('Rmax').innerHTML='最小 '+fmtNum(minR, 8.3).trim()+' 最大 '+fmtNum(maxR, 8.3).trim()+' 平均 '+fmtNum(avgR, 8.3).trim()
var Fxyz=Natm+8+'\nMol\n'
for(i=0; i<Natm; i++) {
Fxyz += Satm[i]+' '+Xatm[i]+' '+Yatm[i]+' '+Zatm[i]+'\n'
}
var Vbox=[ [0,0,0], [1,0,0], [0,1,0], [1,1,0], [0,0,1], [1,0,1], [0,1,1], [1,1,1] ]
for(i=0; i<Vbox.length; i++) {
Fxyz +=
'Uuo '+(minRx+Vbox[i][0]*Xbox)+' '+(minRy+Vbox[i][1]*Ybox)+' '+(minRz+Vbox[i][2]*Zbox)+'\n'
}
ChemDoodle.ELEMENT['Uuo'].covalentRadius=.01
ChemDoodle.ELEMENT['Uuo'].vdWRadius=.01
ChemDoodle.ELEMENT['Uuo'].valency=0
ChemDoodle.ELEMENT['Uuo'].jmolColor="#fff"
molxyz=ChemDoodle.readXYZ(Fxyz)
var o = [-Xbox/2, -Ybox/2, -Zbox/2];
var unitCellVectors = {
o : o,
x : [ o[0] + Xbox, o[1], o[2] ] ,
y : [ o[0], o[1] + Ybox, o[2] ] ,
z : [ o[0], o[1], o[2] + Zbox ] ,
xy : [ o[0] + Xbox, o[1] + Ybox, o[2] ] ,
xz : [ o[0] + Xbox, o[1], o[2] + Zbox ] ,
yz : [ o[0], o[1] + Ybox, o[2] + Zbox ] ,
xyz : [ o[0] + Xbox, o[1] + Ybox, o[2] + Zbox ]
};
var box=[new ChemDoodle.structures.d3.UnitCell(unitCellVectors)]
let dist=ChemDoodle.structures.d3.Distance, atom=molxyz.atoms
if(labBox1) box.push(new dist(atom[Natm ], atom[Natm+1]))
if(labBox2) box.push(new dist(atom[Natm ], atom[Natm+2]))
if(labBox3) box.push(new dist(atom[Natm ], atom[Natm+4]))
if(labBox4) box.push(new dist(atom[Natm+1], atom[Natm+3]))
if(labBox5) box.push(new dist(atom[Natm+1], atom[Natm+5]))
if(labBox6) box.push(new dist(atom[Natm+2], atom[Natm+3]))
if(labBox7) box.push(new dist(atom[Natm+2], atom[Natm+6]))
if(labBox8) box.push(new dist(atom[Natm+3], atom[Natm+7]))
if(labBox9) box.push(new dist(atom[Natm+4], atom[Natm+5]))
if(labBox10) box.push(new dist(atom[Natm+4], atom[Natm+6]))
if(labBox11) box.push(new dist(atom[Natm+5], atom[Natm+7]))
if(labBox12) box.push(new dist(atom[Natm+6], atom[Natm+7]))
Mol1.loadContent([molxyz], box)
}
function setRad(Irad) {
var ElmMasRad='H 1.007840 1.10 1.10 He 4.002602 1.40 1.40 Li 6.938000 2.14 1.81 Be 9.012183 1.69 1.53 B 10.806000 1.68 1.92 C 12.009600 1.60 1.70 N 14.006430 1.53 1.55 O 15.999030 1.43 1.52 F 18.998403 1.38 1.47 Ne 20.179700 1.54 1.54 Na 22.989769 2.38 2.27 Mg 24.304000 2.00 1.73 Al 26.981538 1.92 1.84 Si 28.084000 1.93 2.10 P 30.973762 1.88 1.80 S 35.446000 1.81 1.80 Cl 39.948000 1.78 1.75 Ar 39.098300 1.63 1.88 K 40.078000 2.52 2.75 Ca 44.955908 2.27 2.31 Sc 47.867000 2.15 0.00 Ti 50.941500 2.11 0.00 V 51.996100 2.07 0.00 Cr 54.938044 2.06 0.00 Mn 55.845000 2.05 0.00 Fe 58.933194 2.04 0.00 Co 58.693400 2.00 0.00 Ni 63.546000 1.97 0.00 Cu 65.380000 1.96 0.00 Zn 69.723000 2.01 0.00 Ga 72.630000 2.03 1.87 Ge 74.921595 2.05 2.11 As 78.971000 2.08 1.85 Se 79.901000 1.94 1.90 Br 83.798000 1.92 1.83 Kr 85.467800 1.84 2.02 Rb 87.620000 2.61 3.03 Sr 88.905840 2.42 2.49 Y 91.224000 2.32 0.00 Zr 92.906370 2.23 0.00 Nb 95.950000 2.18 0.00 Mo 0.000000 2.17 0.00 Tc 101.070000 2.16 0.00 Ru 102.905500 2.13 0.00 Rh 106.420000 2.10 0.00 Pd 107.868200 2.10 0.00 Ag 112.414000 2.11 0.00 Cd 114.818000 2.18 0.00 In 118.710000 2.21 1.93 Sn 121.760000 2.23 2.17 Sb 127.600000 2.24 2.06 Te 126.904470 2.16 2.06 I 131.293000 2.11 1.98 Xe 132.905452 2.16 2.16 Cs 138.905470 2.75 3.43 Ba 140.116000 2.59 2.68 La 140.907660 2.43 0.00 Ce 144.242000 2.42 0.00 Pr 0.000000 2.40 0.00 Nd 150.360000 2.39 0.00 Pm 151.964000 2.38 0.00 Sm 157.250000 2.36 0.00 Eu 158.925350 2.35 0.00 Gd 162.500000 2.34 0.00 Tb 164.930330 2.33 0.00 Dy 167.259000 2.31 0.00 Ho 168.934220 2.30 0.00 Er 173.045000 2.29 0.00 Tm 174.966800 2.27 0.00 Yb 178.490000 2.26 0.00 Lu 180.947880 2.24 0.00 Hf 183.840000 2.23 0.00 Ta 186.207000 2.22 0.00 W 190.230000 2.15 0.00 Re 192.217000 2.16 0.00 Os 195.084000 2.16 0.00 Ir 196.966569 2.13 0.00 Pt 200.592000 2.13 0.00 Au 204.382000 2.14 0.00 Hg 207.200000 2.23 0.00 Tl 208.980400 2.27 1.96 Pb 0.000000 2.37 2.02 Bi 0.000000 2.38 2.07 Po 0.000000 2.49 1.97 At 0.000000 2.36 2.02 Rn 0.000000 2.43 2.20 Fr 0.000000 3.15 3.48 Ra 232.037700 2.83 2.83 Ac 231.035880 2.47 0.00 Th 238.028910 2.45 0.00 Pa 0.000000 2.43 0.00 U 0.000000 2.41 0.00 Np 0.000000 2.39 0.00 Pu 0.000000 2.37 0.00 Am 0.000000 2.35 0.00'.split(/\s+/)
var ret=''
if(Irad==0) {
for(i=0; i<ElmMasRad.length; i+=4) {
ret += fmtStr(ElmMasRad[i], 2)+' '+ElmMasRad[i+1]+' '+ElmMasRad[i+2]+'\n'
}
} else {
for(i=0; i<ElmMasRad.length; i+=4) {
ret += fmtStr(ElmMasRad[i], 2)+' '+ElmMasRad[i+1]+' '+ElmMasRad[i+3]+'\n'
}
}
$('masrad').value=ret
}
function fmtStr(str, num) {
return str.length>num ? str : str+Array(num-str.length+1).join(' ')
}
function fmtNum(num, fmt) {
var fmt=String(fmt), m=fmt.split(".")[0]
num=num.toFixed(fmt.split(".")[1])
if(num.length<m) num=Array(m-num.length+1).join(" ")+num
return num
}
function dot(A, B) { return A[0]*B[0]+A[1]*B[1]+A[2]*B[2] }
function Jacobi(A, Q, W) {
/* ----------------------------------------------------------------------------
Calculates the eigenvalues and normalized eigenvectors of a symmetric 3x3
matrix A using the Jacobi algorithm.
The upper triangular part of A is destroyed during the calculation,
the diagonal elements are read but not destroyed, and the lower
triangular elements are not referenced at all.
----------------------------------------------------------------------------
Parameters:
A: The symmetric input matrix
Q: Storage buffer for eigenvectors
W: Storage buffer for eigenvalues
----------------------------------------------------------------------------*/
var N=3, Reps=1E-10, maxIter=100, i, j, k, tmp, S, C, T, G, H, Z, Roff, tht, tol
//Initialize Q to the identitity matrix, W to diag(A)
for(i=0; i<N; i++) { W[i] = A[i][i]; Q[i]=[]; Q[i][i]=1 }
for(i=0; i<N; i++) { for(j=0; j<i; j++) {
Q[i][j] = 0
Q[j][i] = 0
}}
//Main iteration loop
for(var Iter=1; Iter<maxIter; Iter++) {
//Test for convergence
Roff = 0
for(i=0; i<N; i++) { for(j=i+1; j<N; j++) {
Roff += Math.abs(A[i][j])
}}
if(Math.abs(Roff)<Reps) {
for(i=0; i<N; i++) {
for(j=0; j<N-1; j++) { //sort
if(W[j]>W[j+1]) {
k=W[j]
W[j]=W[j+1]
W[j+1]=k
k = [ Q[j][0], Q[j][1], Q[j][2] ]
Q[j]=Q[j+1]
Q[j+1]=k
}
}
} // asure RIGHT-HAND axis
if( Q[1-1][1-1]*(Q[2-1][2-1]*Q[3-1][3-1]-Q[2-1][3-1]*Q[3-1][2-1])
-Q[1-1][2-1]*(Q[2-1][1-1]*Q[3-1][3-1]-Q[2-1][3-1]*Q[3-1][1-1])
+Q[1-1][3-1]*(Q[2-1][1-1]*Q[3-1][2-1]-Q[2-1][2-1]*Q[3-1][1-1]) <0) {
Q[0]= [ -Q[0][0], -Q[0][1], -Q[0][2] ]
Q[1]= [ -Q[1][0], -Q[1][1], -Q[1][2] ]
Q[2]= [ -Q[2][0], -Q[2][1], -Q[2][2] ]
}
return Iter
}
tol = 0
if(Iter<4) tol = 0.2*Roff/(N*N)
//Do sweep
for(i=0; i<N; i++) {
for(j=i+1; j<N; j++) {
G = 100 * Math.abs(A[i][j])
if(Iter>4 && Math.abs(W[i])+G==Math.abs(W[i])
&& Math.abs(W[j])+G==Math.abs(W[j])) {
A[i][j] = 0
} else if(Math.abs(A[i][j])>tol) {
//Calculate Jacobi transformation
H = W[j] - W[i]
if(Math.abs(H)+G==Math.abs(H)) {
T = A[i][j]/H
} else {
tht = 0.5 * H/A[i][j]
T = 1/( Math.abs(tht) + Math.sqrt(1+tht*tht) )
if(tht<0.) T = -T
}
C = 1/Math.sqrt(1+T*T)
S = T * C
Z = T * A[i][j]
//Apply Jacobi transformation
A[i][j] = 0.
W[i] -= Z
W[j] += Z
for(k=0; k<i; k++) {
T = A[k][i]
A[k][i] = C * T - S * A[k][j]
A[k][j] = S * T + C * A[k][j]
}
for(k=i+1; k<j; k++) {
T = A[i][k]
A[i][k] = C * T - S * A[k][j]
A[k][j] = S * T + C * A[k][j]
}
for(k=j+1; k<N; k++) {
T = A[i][k]
A[i][k] = C * T - S * A[j][k]
A[j][k] = S * T + C * A[j][k]
}
//Update eigenvectors
for(k=0; k<N; k++) {
T = Q[i][k]
Q[i][k] = C * T - S * Q[j][k]
Q[j][k] = S * T + C * Q[j][k]
}
}
}
}
}
return 0
}
</script>
参考资料

