layout: post title: 分子模拟周刊：第 12 期 categories:
谁是我们的敌人？谁是我们的朋友？这个问题是革命的首要问题。中国过去一切革命斗争成效甚少，其基本原因就是因为不能团结真正的朋友，以攻击真正的敌人。革命党是群众的向导，在革命中未有革命党领错了路而革命不失败的。我们的革命要有不领错路和一定成功的把握，不可不注意团结我们的真正的朋友，以攻击我们的真正的敌人。
——《毛泽东选集·中国社会各阶级的分析》
毛泽东选集 的第一篇文章或许也是其中最有名的一篇, 因为于一本书而言, 第一页给人的印象总是很深, 就像我至今还记得英语四六级单词书第一页的第一个单词, Abandon.
这篇文章指出的问题, 不仅适用于革命年代, 也适用于如今的时代. 从个人, 到家庭, 到企业, 到国家, 对中国或任何国家, 这个问题仍然存在: 我们到底要依靠谁, 谁才是我们的力量之源?
我记得看过一部电影, 大约是 爱国者 吧, 具体情节早已经模糊了, 却还记得主角要召集参战者的时候, 没有去找那些生活优渥的人, 而是去了下层人物聚集的小酒馆.
多年前, 我也读过 围城, 其中讲的那些幽默段子, 掉的那些书袋, 我早就忘记了. 但现今我还记得, 即便是在抗战的时候, 官太太们仍然在可以飞来飞去, 买卖风生水起.
中国有句话, 仗义每多屠狗辈, 负心多是读书人. 我读书不多, 不敢枉称读书人, 却也经常以此自戒.
我们的中国, 过去的中国, 现今的中国, 未来的中国, 所能依靠的, 仍然是那些植根于其中的人. 他们或许没有办法轻易迁移, 但正因了这, 才让他们成为了泰坦中国脚下的盖娅.
我们不能只欣赏海面的高高浪花, 而忘记了下面幽深不可见的水. 正是因为有了巨量的底水, 才能掀起高高的浪花. 这沉默的大多数, 是真的在沉默, 还是在积蓄滔天的力量呢?
收录马列著作很全的网站, 需要的时候可以查看.
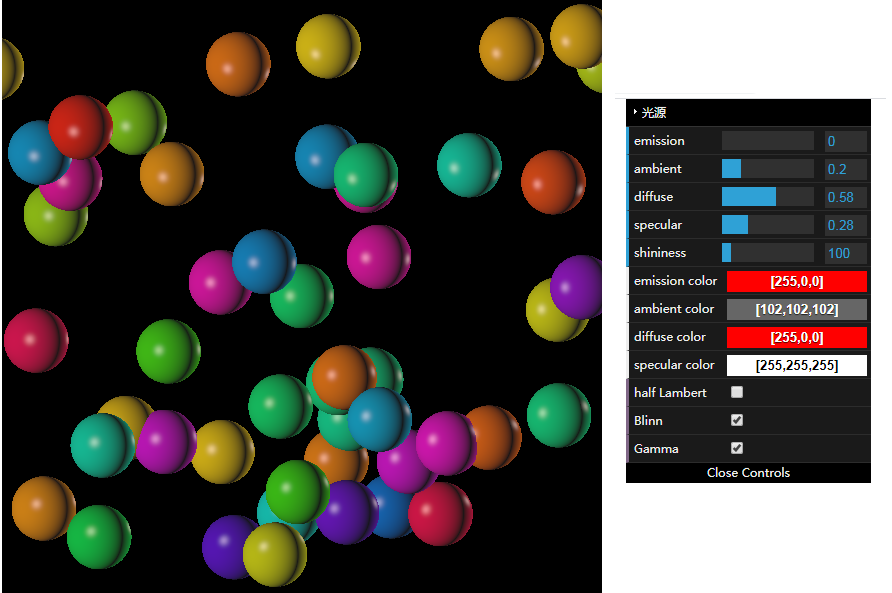
我一直在断断续续地学习图形学的知识, 主要是webGL. 在学习的过程中, 我觉得需要将学到的东西慢慢转化为一个完整的项目, 这样可以加深理解, 也能够增强我的代码能力. 目前主要着眼于着色器, 完成了Phong着色器.
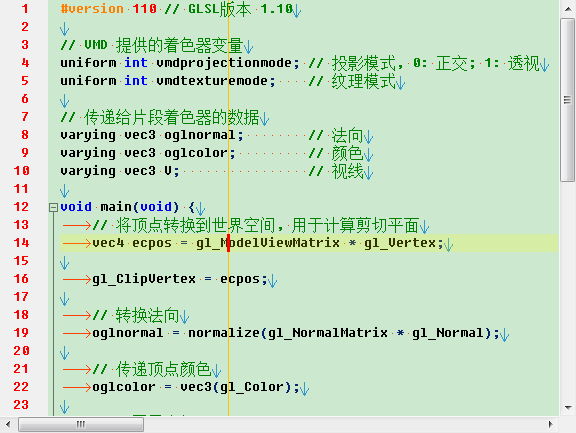
既然我在学习着色器的知识, 也顺便学习了一下VMD自带的着色器代码, 并添加了注释, 方便理解. 弄清楚了VMD的着色器, 也就明白了VMD默认的显示效果为什么不很漂亮.
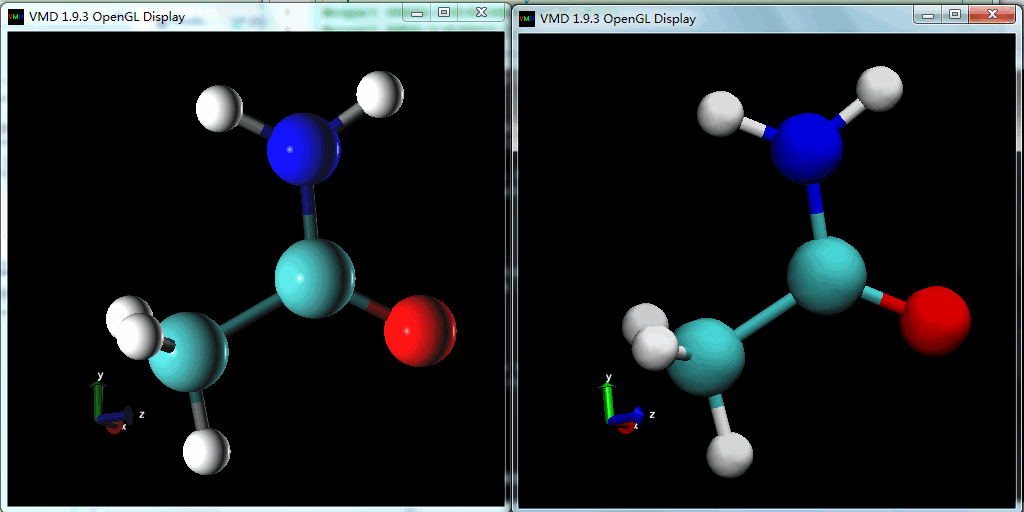
既然我已经会写Phong着色器代码, 也明白VMD的着色器实现了, 那就让VMD来使用我自己的Phong着色器吧. 试用了一下, 比默认的显示效果好了不少, 接近PyMOL的默认效果了.
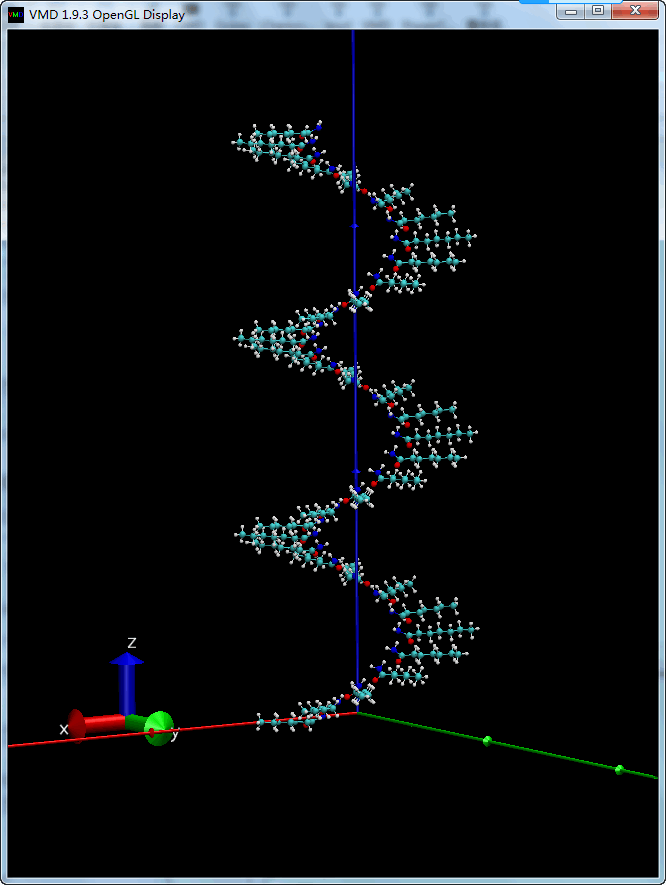
整理了VMD手册中向量与矩阵操作的文档, 并以具体实例说明了如何使用它们创建特殊的体系. 如果你需要使用VMD建模特殊结构, 那就好好学习下吧.
学艺术和建筑的, 经常要外出采风和写生. 做科研的也同样需要, 只不过换成了阅读文献和查看问题. 阅读别人的论文其实就是采风, 而尝试解决别人提出的问题, 就是写生了.
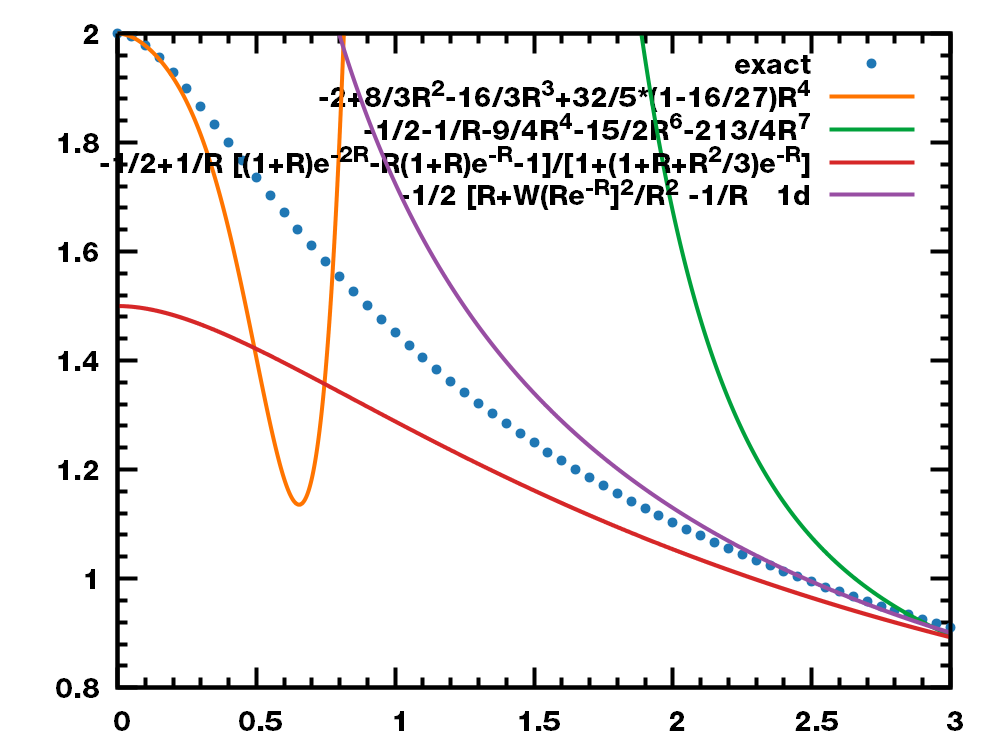
这个星期继续我对氢分子离子H2+精确解的探索, 先是找到了势能曲线的精确数值解
然后对比了一下一些近似解与数值解. 在核间距很大的情况下, 基于微扰和一维模型的近似解都可以符合的很好. 对于核间距很小的情况, 势能曲线应该接近二次函数, 微扰解符合二次函数, 但数值不对; 一维模型解发散. 能不能找到一个近似解, 在整个核间距范围内都符合得很好, 且趋势正确呢? 这并不像看起来那么简单.
这个问题有年头了, 问过的人也不在少数, 但到目前也没有太好的解决方法, 因为每个粒子不是固定于某层的, 所以要处理只能采用类似计算滞留时间的方法, 比较麻烦. 文献上还有其他的一些处理方法, 看起来都比较复杂. 我一直在找机会把这个问题处理一下, 可大多数问这个问题的人也就只是问问, 并不见得真是铁了心要把它解决掉. 既然如此, 我又何必越粗代庖呢?
这是拟合力场参数的最简单情况, 只有一项相互作用.
由于
Eqm(phi)-Eqm(phi0)=Emm(phi)-Emm(phi0)=Umm(all\phi)+U(phi)
所以要拟合的量为
U(phi)=Eqm(phi)-Eqm(phi0)-Umm(all\phi)
本周刊记录我每周所读所思, 并自觉值得与大家分享的内容.
本周刊同步更新在我的网络日志 哲·科·文 和微信公众号 分子模拟之道.
如果你觉得我的分享对你有益, 不妨将它推荐给你认识的人.
如果你也认同分享的理念, 欢迎投稿或推荐自己的内容. 请关注微信公众号后台留言, 或加入QQ群联系.