仓库源文，站点原文

layout: post title: 剪切模量各向异性 categories:

• 科 tags:
• matlab
• 编程 math: true

• 2014-10-03 10:10:58 硕士生 伊国辉 对此文有所贡献
• 2017-07-19 10:32:41 与弹性模量代码合并
• 2018-07-20 09:21:44 三斜晶系剪切模量代码, 感谢 陈磊 提供信息

以前的博文中讲过用matlab作弹性模量(杨氏模量)的各向异性图，这里更进一步, 讲讲剪切模量各向异性的作图。

我们知道，剪切模量定义为: 在某个晶面上沿着某一特定方向施加剪切应力后剪切应力和应变的比值。它的值是和两个方向有关的.

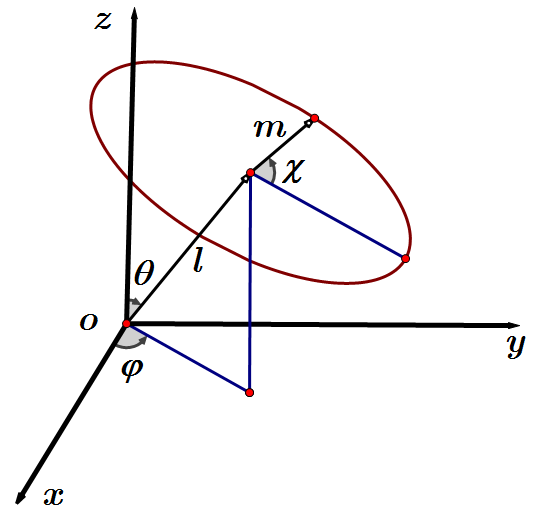
在图中，与向量 $l$ 垂直的平面即是晶体要发生剪切的平面. 由于弹性模量的各向异性，在这一特定平面的不同方向， 施加相同的剪切应力会得到不同的剪切应变，故会得到不同的剪切模量的值。此外, 与杨氏模量不同的是，剪切模量在某一方向 $l$ 上的值还与角度 $\chi$ 有关. 这就导致剪切模量的各向异性比杨氏模量更加复杂。

虽然剪切模量的各项异性比杨氏模量复杂, 但是作图的方法没有什么本质区别. 作图的关键是它的计算.

以立方晶系为例, 其杨氏模量

$$E= S{11}-2(S{11}-S{12}-{1 \over 2}S{44})(l_1^2l_2^2+l_1^2l_3^2+l_2^2l_3^2)$$

相应的剪切模量为

$$\begin{align} G &=4S_{11}(l_1^2m_1^2+l_2^2m_2^2+l_3^2m3^2) \ &+ 8S{12}(l_1l_2m_1m_2 +l_1l_3m_1m_3+l_2l_3m_2m3) \ &+ S{44}[(l_1m_2+l_2m_1)^2+(l_1m_3+l_3m_1)^2+(l_2m_3+l_3m_2)^2] \ &= A m_1^2 + B m_2^2 + C m_3^2 + 2D m_1m_2 + 2E m_1m_3 +2F m_2m_3 \end{align}$$

其中

$$l=\left( \begin{matrix} \sin \theta \cos \phi \ \sin \theta \sin \phi \ \cos \theta \ \end{matrix} \right);\quad m=\left( \begin{matrix} \cos \theta \cos \phi \cos \chi -\sin \phi \sin \chi \ \cos \theta \sin \phi \cos \chi +\cos \phi \sin \chi \ -\sin \theta \cos \chi \ \end{matrix} \right)$$

通常对剪切模量进行表征时使用其在每一方向上最大值或最小值, 这就需要我们计算剪切模量某一方向的极值.

若令 $$\a=4S{11}-S{44}, \b=4S{12}+S{44}, \g=S_{44}$$, 则 $G$ 可写为

$$G= A m_1^2 + B m_2^2 + C m_3^2 + 2D m_1m_2 + 2E m_1m_3 +2F m_2m_3$$

其中

$$\begin{align} A &= \a l1^2+\g=(4S{11}-S_{44})l_1^2+S44 \ B &= \a l_1^2+\g \ C &= \a l_1^2+\g \ D &= \b l_1l2 = (4S{12}+S_{44})l_1l_2 \ E &= \b l_1l_3 \ F &= \b l_2l_3 \end{align}$$

可见 $G$ 为 $m_1, m_2, m_3$ 的二次型, 可根据其正定性判断极值情况.

根据极值的必要条件, 也可对 $G$ 进行求导, 根据 $m_1, m_2, m_3$ 方程组解的情况进行判断极值情况. 求导后

$$\begin{bmatrix} A & D & E \ D & B & F \ E & F & C \ \end{bmatrix} \left[ \begin{array}{c} m_1 \ m_2 \ m_3 \end{array} \right] =0$$

其行列式

$$\D = (\a^3+2\b^3-3\a\b^2)l_1^2l_2^2l_3^2 + \g(\a^2-\b^2)(l_1^2l_2^2+l_1^2l_3^2+l_2^2l_3^2)+\a\g^2+\g^3$$

这两种情形下, 得到的极值点都为 $(0, 0, 0)$, 但显然无法满足 $m_1^2+m_2^2+m_3^2=1$ 的约束条件, 所以这两种方法都不可行.

换用最笨的方法, 直接将 $m_i$ 的表达式代入, 化简后得到 $G$ 满足的方程. 设

$$\alg m_1 &= \cos \theta \cos \phi \cos \chi -\sin \phi \sin \chi = P \cos\chi + Q \sin\chi \ m_2 &= \cos \theta \sin \phi \cos \chi +\cos \phi \sin \chi = R \cos\chi + S \sin\chi \ m_3 &= -\sin \theta \cos \chi = T \cos\chi \ealg$$

则

$$\alg G &= (APQ + BRS + DPS + DQR + EQT + FST) \sin(2x) \ &+ (AP^2 + BR^2 + CT^2 + 2DPR + 2EPT + 2FRT ) \cos^2 x \ &+ (AQ^2 + BS^2 + 2DQS ) \sin^2 x \ &= C_1 \sin(2x) + C_2 \cos^2 x + C_3 \sin^2 x \ &= C_1 \sin(2x) + (C_2-C3) \cos^2 x + C_3 \ &= C_1 \sin(2x) + {C_2-C_3 \over 2} \cos(2x) + {C_2+C_3 \over 2} \ &= \sqrt{C_1^2+{(C_2-C_3)^2 \over 4}} \sin(2x+\f) + {C_2+C_3 \over 2} , \f= \arctan {C_2-C_3 \over 2 C_1} \ealg$$

最终表示为简单的三角函数, 容易知道, $G$ 的最大值

$G_{max}={C_2+C_3 \over 2}+\sqrt{C_1^2+{(C_2-C_3)^2 \over 4}}$

最小值

$G_{min}= {C_2+C_3 \over 2} - \sqrt{C_1^2+{(C_2-C_3)^2 \over 4}}$

上面的推导过程可借助matlab的符号计算功能完成.

虽然有了解析的表达式, 但实际编码时很繁琐, 且大多数情况下我们并不能得到解析的公式. 所以这只是作为求极值的一种方法. 常用的数值方法中最简单的就是分割点直接计算所有值, 然后求其最大值或最小值, 复杂一点的就是利用优化的各种方法.

推广一下, 对三斜晶系, 剪切模量计算公式为

$$\alg 1/G = &4 [S_{11} (l_1 m1)^2 + S{22} (l_2 m2)^2 + S{33} (l_3 m3)^2] \ +&S{44} (l_2 m_3+l_3 m2)^2 + S{55} (l_1 m_3+l_3 m1)^2 + S{66} (l_1 m_2+l_2 m1)^2 \ +&8 [ S{12} (l_1 l_2 m_1 m2) + S{13} (l_1 l_3 m_1 m3) + S{23} (l_2 l_3 m_2 m_3) ] \ +&4 l_1 m1 [S{14} (l_2 m_3+l_3 m2)+S{15} (l_1 m_3+l_3 m1)+S{16} (l_1 m_2+l_2 m_1)] \ +&4 l_2 m2 [S{24} (l_2 m_3+l_3 m2)+S{25} (l_1 m_3+l_3 m1)+S{26} (l_1 m_2+l_2 m_1)] \ +&4 l_3 m3 [S{34} (l_2 m_3+l_3 m2)+S{35} (l_1 m_3+l_3 m1)+S{36} (l_1 m_2+l_2 m1)] \ +&2 \quad \quad \;S{45} (l_2 m_3+l_3 m_2) (l_1 m_3+l_3 m1) \ +&2 \quad \quad \;S{46} (l_2 m_3+l_3 m_2) (l_1 m_2+l_2 m1) \ +&2 \quad \quad \;S{56} (l_1 m_3+l_3 m_1) (l_1 m_2+l_2 m1) \ = & S{11} A{11}^2 + S{22} A{22}^2 + S{33} A{33}^2 + S{44} A{23}^2 + S{55} A{13}^2 + S{66} A{12}^2 \ +&2 [ S{12} A{11} A{22} + S{13} A{11} A{33}+ S{23} A{22} A{33} ] \ +&2 A{11} [S{14} A{23} + S{15} A{13}+S{16} A{13}] \ +&2 A{22} [S{24} A{23} + S{25} A{13}+S{26} A{13}] \ +&2 A{33} [S{34} A{23} + S{35} A{13}+S{36} A{13}] \ +&2 S{45} A{23} A{13} + 2 S{46} A{23} A{12} + 2 S{56} A{13} A{12} \ \ A_{ij}=&l_i m_j+l_j m_i \ealg$$

因为 $\vec l$ 与 $\vec m$ 垂直, 因此其点积 $l_1m_1+l_2m_2+l_3m_3=0$, 利用此条件, 可以得到上式的另一种形式:

$$\alg 1/G= &4 [2 S{12}-(S{11}+S{22}-S{66})] l_1 m_1 l_2 m2 \ +&4 [2 S{23}-(S{22}+S{33}-S_{44})] l_2 m_2 l_3 m3 \ +&4 [2 S{13}-(S{33}+S{11}-S_{55})] l_1 m_1 l_3 m_3 \ +&4 (l_1 m_2+l_2 m1) [(S{16}-S_{36}) l_1 m1+(S{26}-S_{36}) l_2 m_2] \ +&4 (l_2 m_3+l_3 m2) [(S{24}-S_{14}) l_2 m2+(S{34}-S_{14}) l_3 m_3] \ +&4 (l_1 m_3+l_3 m1) [(S{35}-S_{25}) l_3 m3+(S{15}-S_{25}) l_1 m1] \ +& \;\; S{44} (l_2 m_3-l_3 m2)^2 \ +& \;\; S{55} (l_3 m_1-l_1 m3)^2 \ +& \;\; S{66} (l_1 m_2-l_2 m1)^2 \ +&2 S{45} (l_2 m_3+l_3 m_2) (l_1 m_3+l_3 m1) \ +&2 S{46} (l_2 m_3+l_3 m_2) (l_1 m_2+l_2 m1) \ +&2 S{56} (l_1 m_3+l_3 m_1) (l_1 m_2+l_2 m_1) \ealg$$

照例, 下面给出几种典型金属的剪切模量最大值与最小值的图像, 前者为最大值, 后者为最小值.

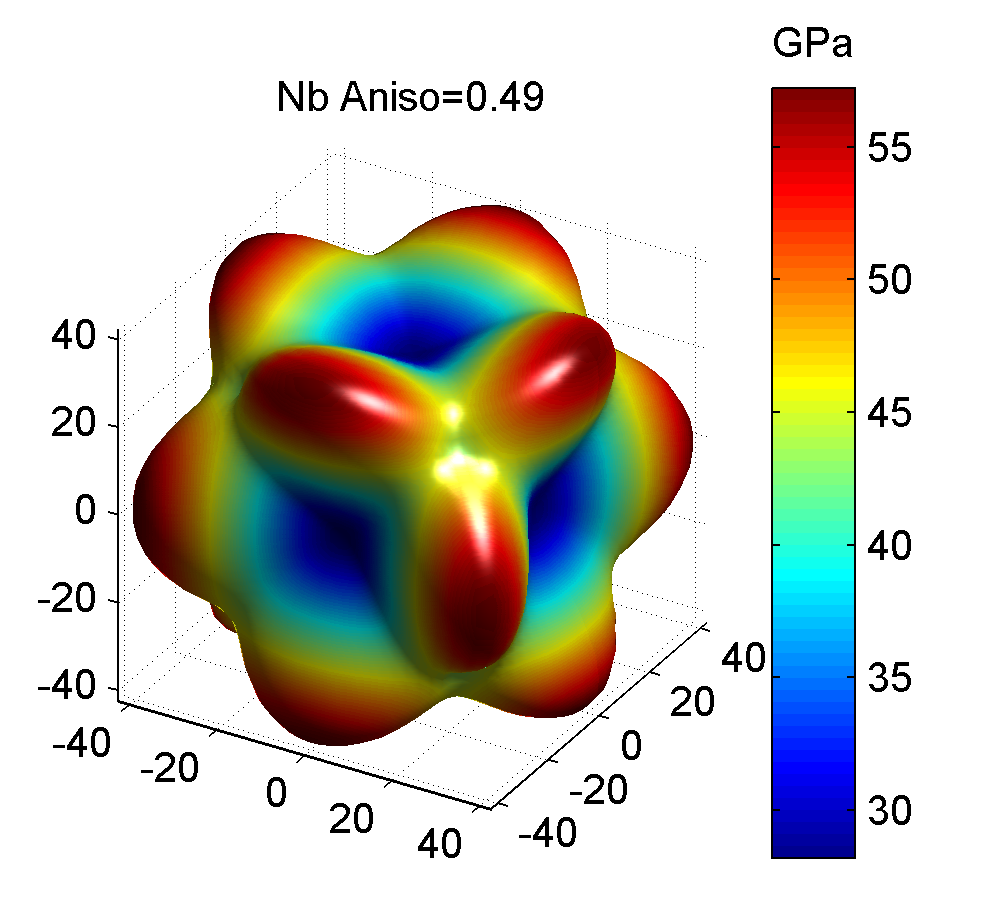
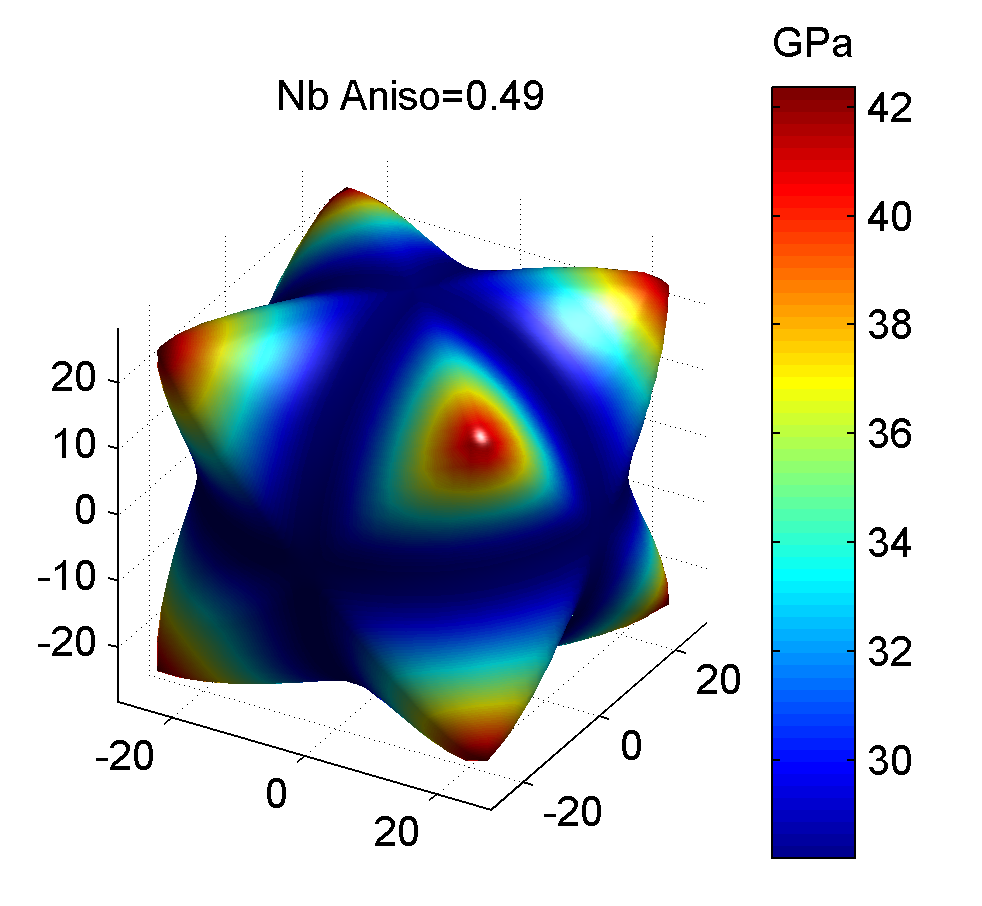
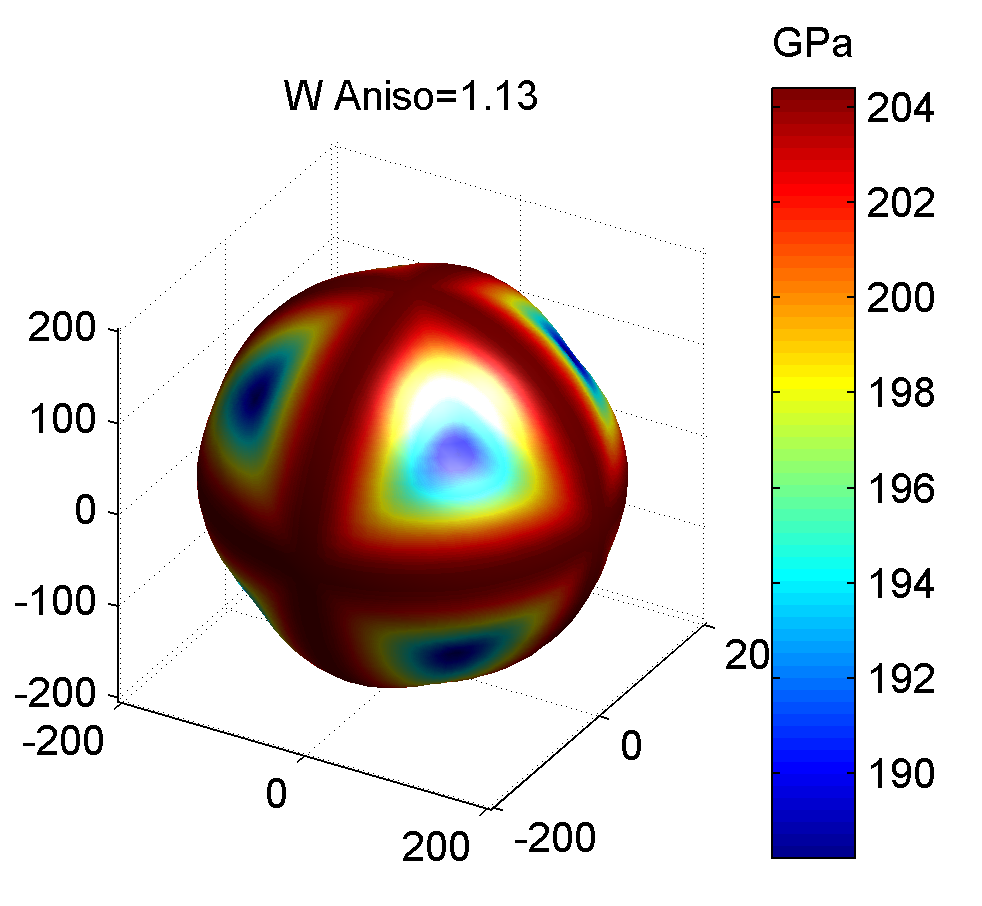
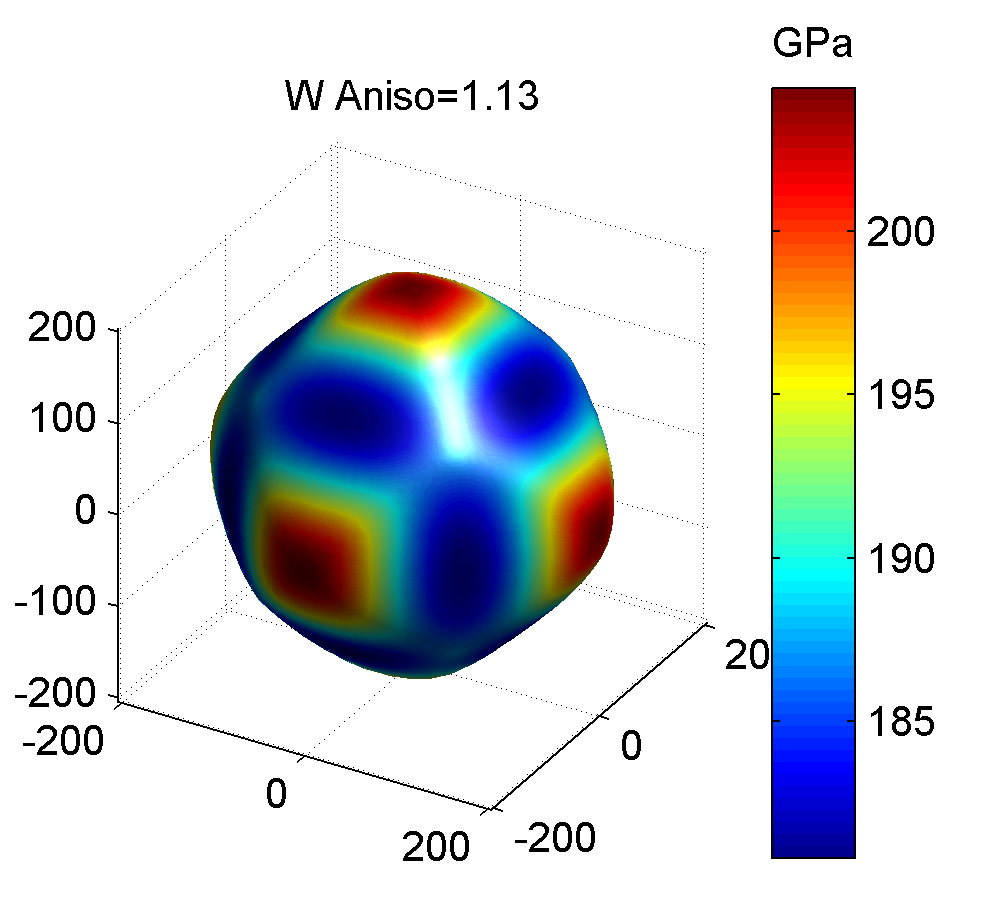
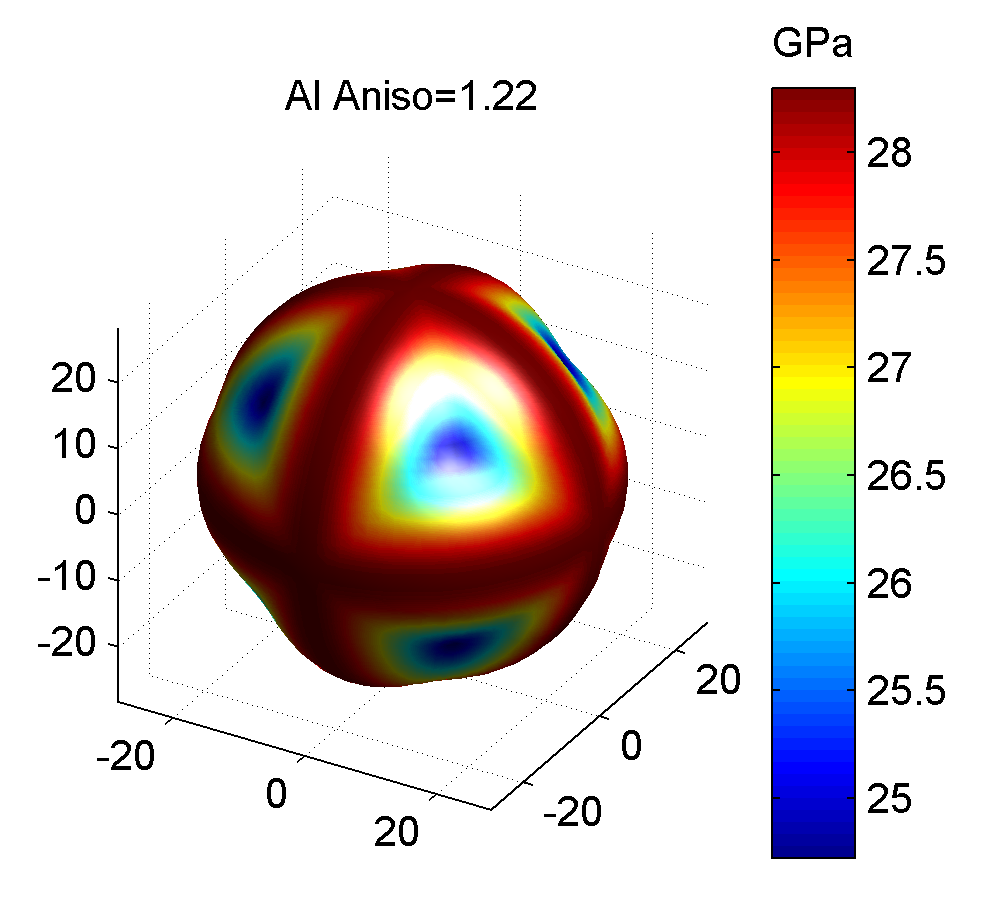
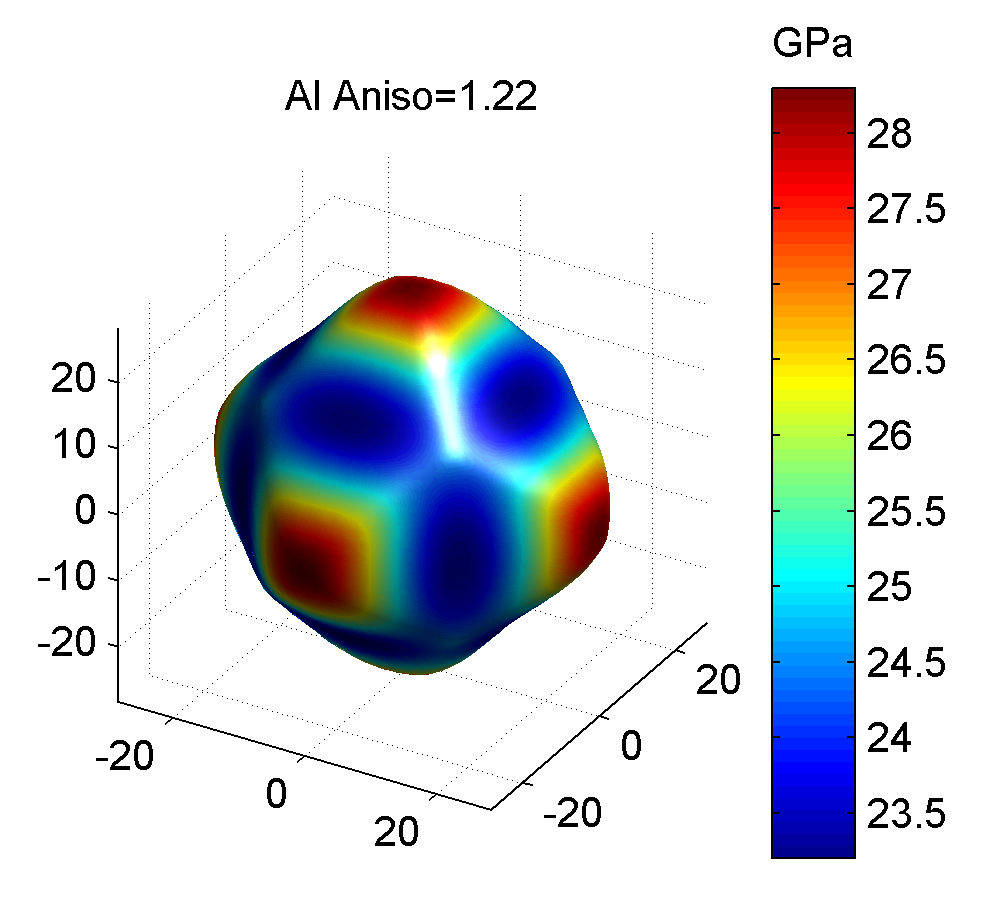
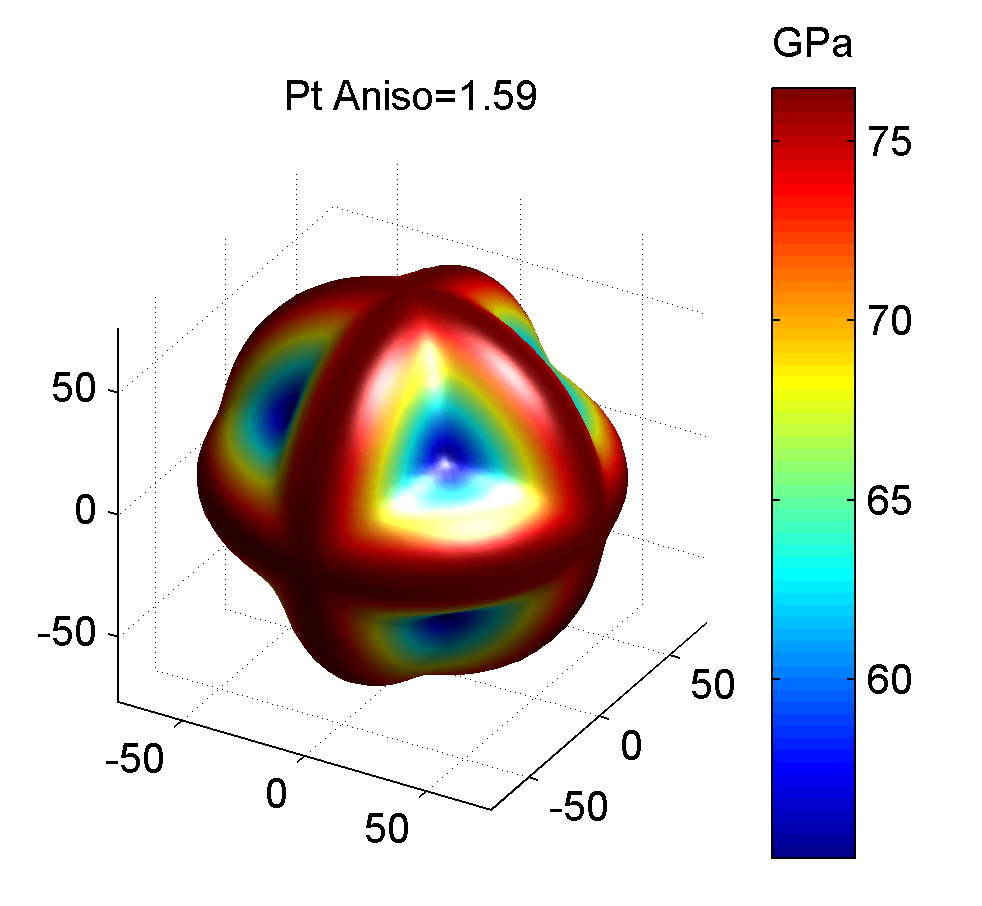
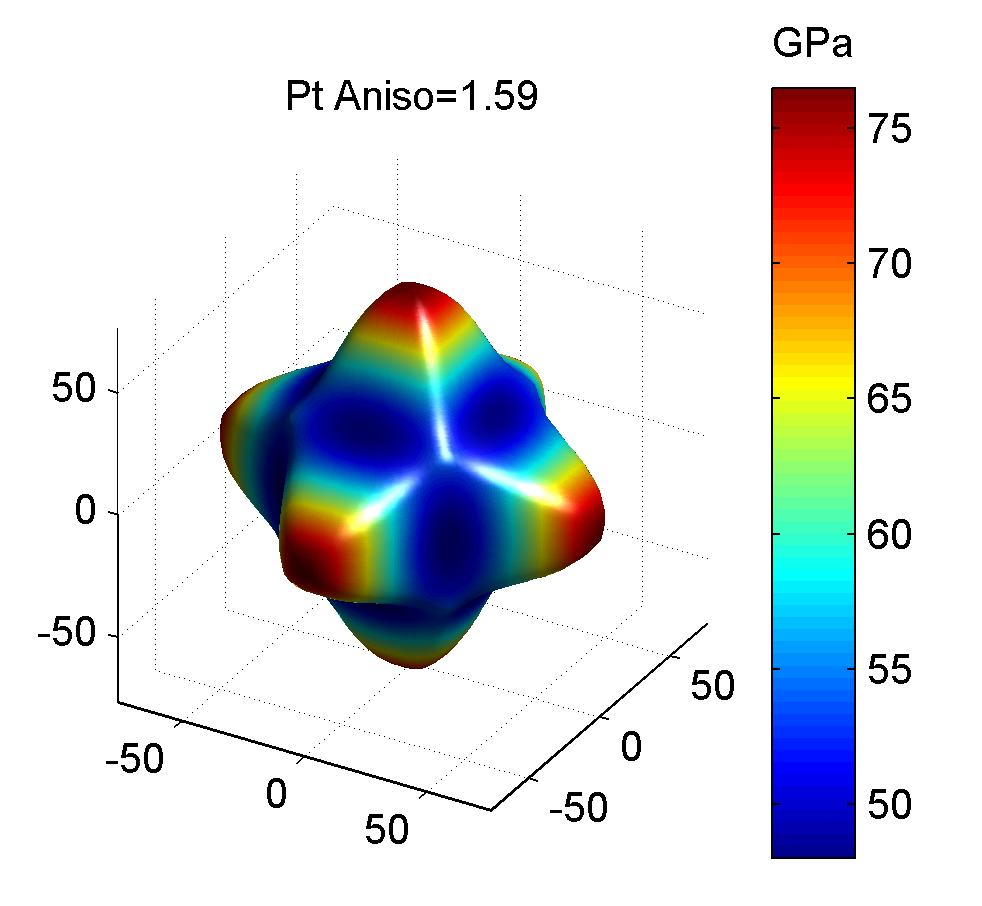
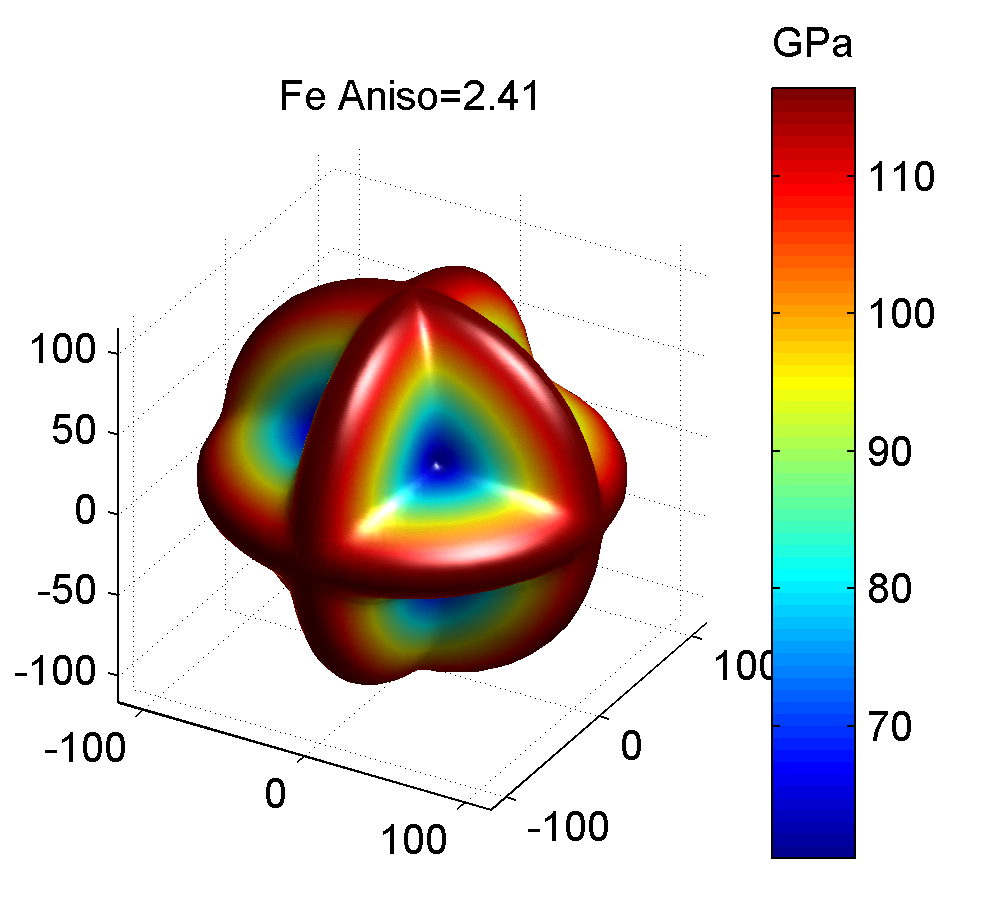
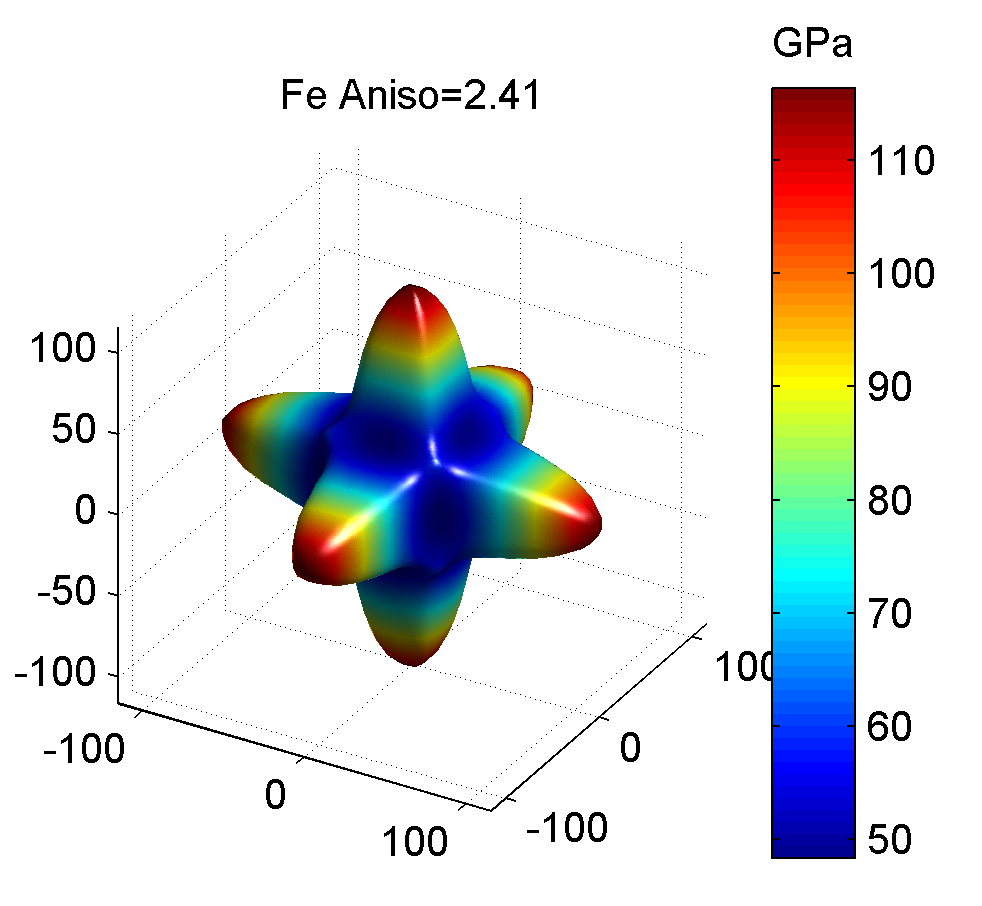
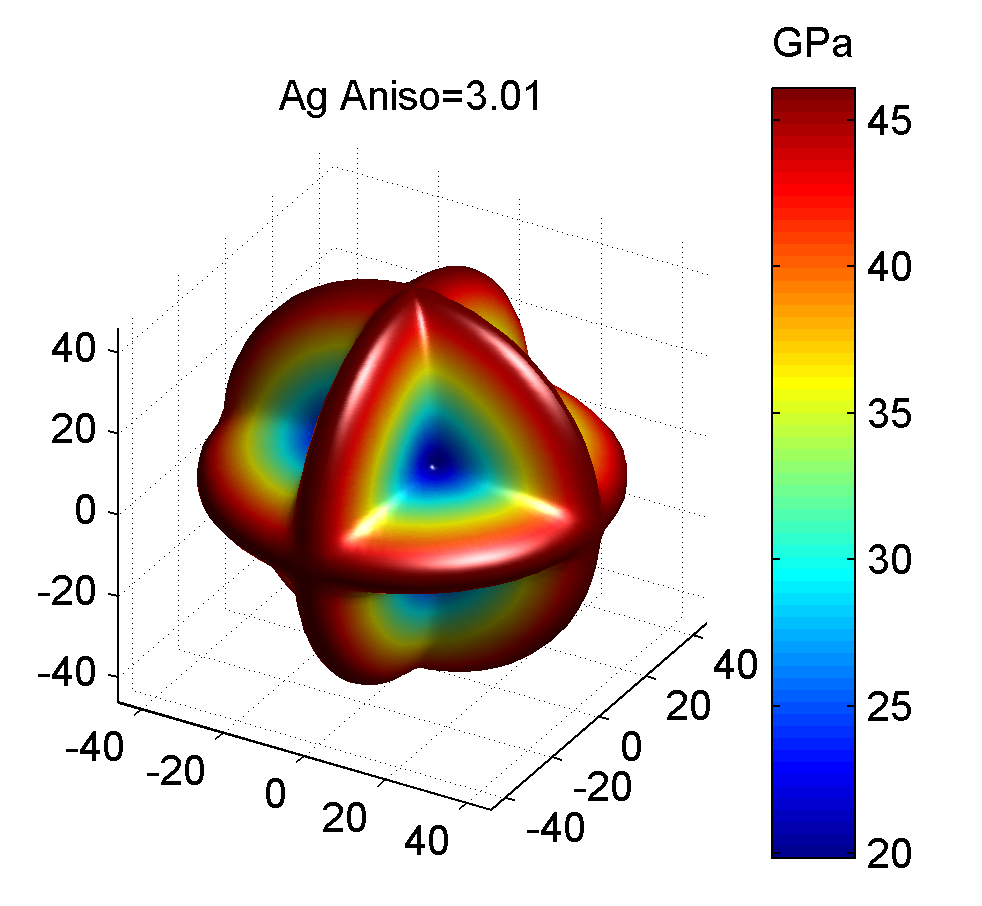
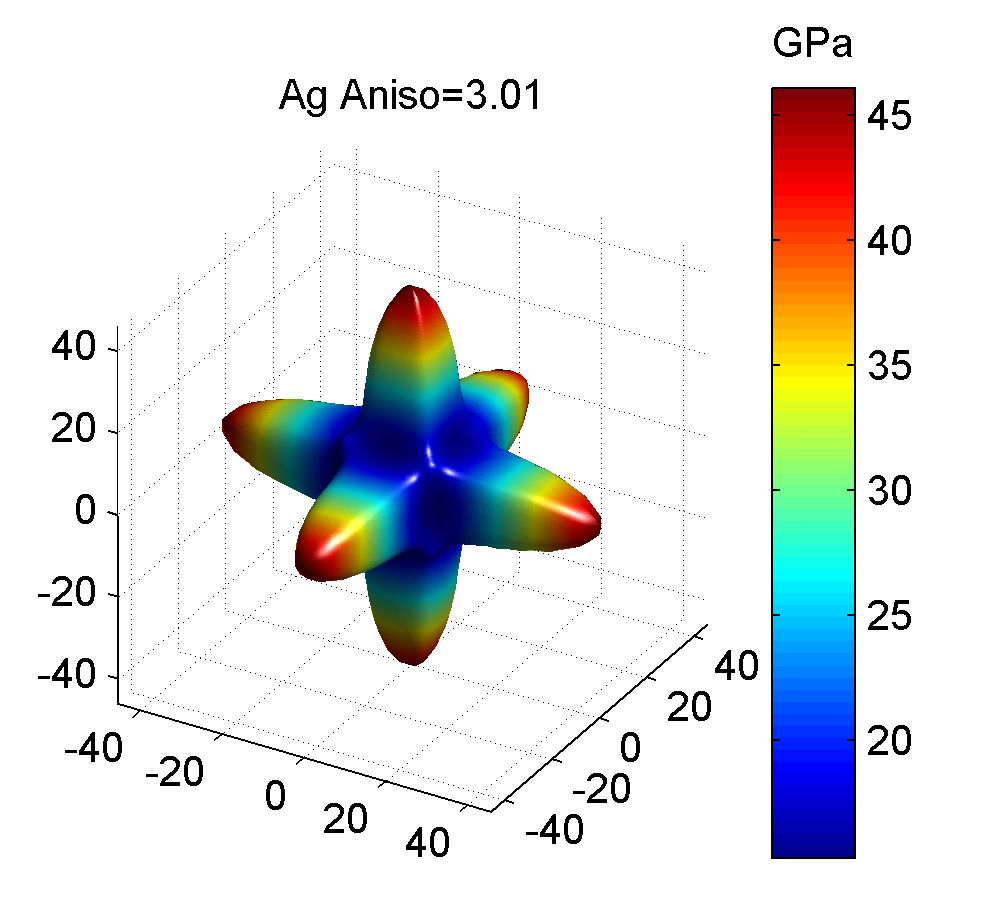
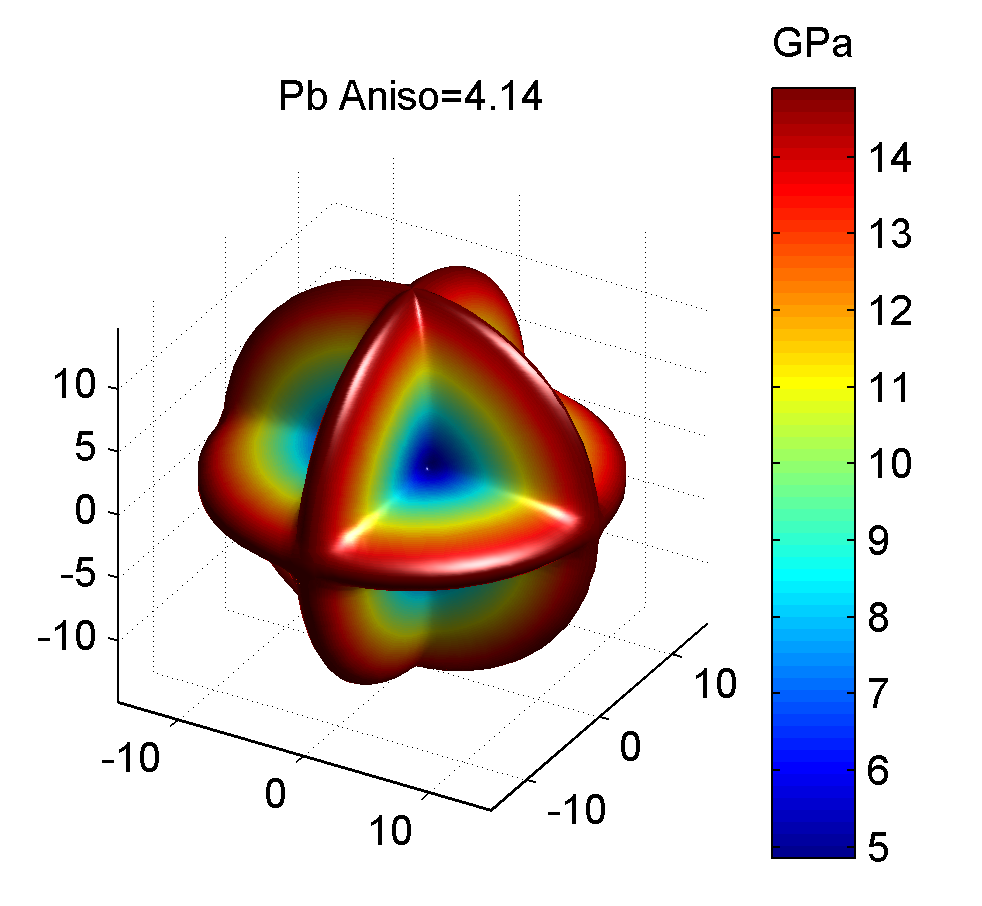
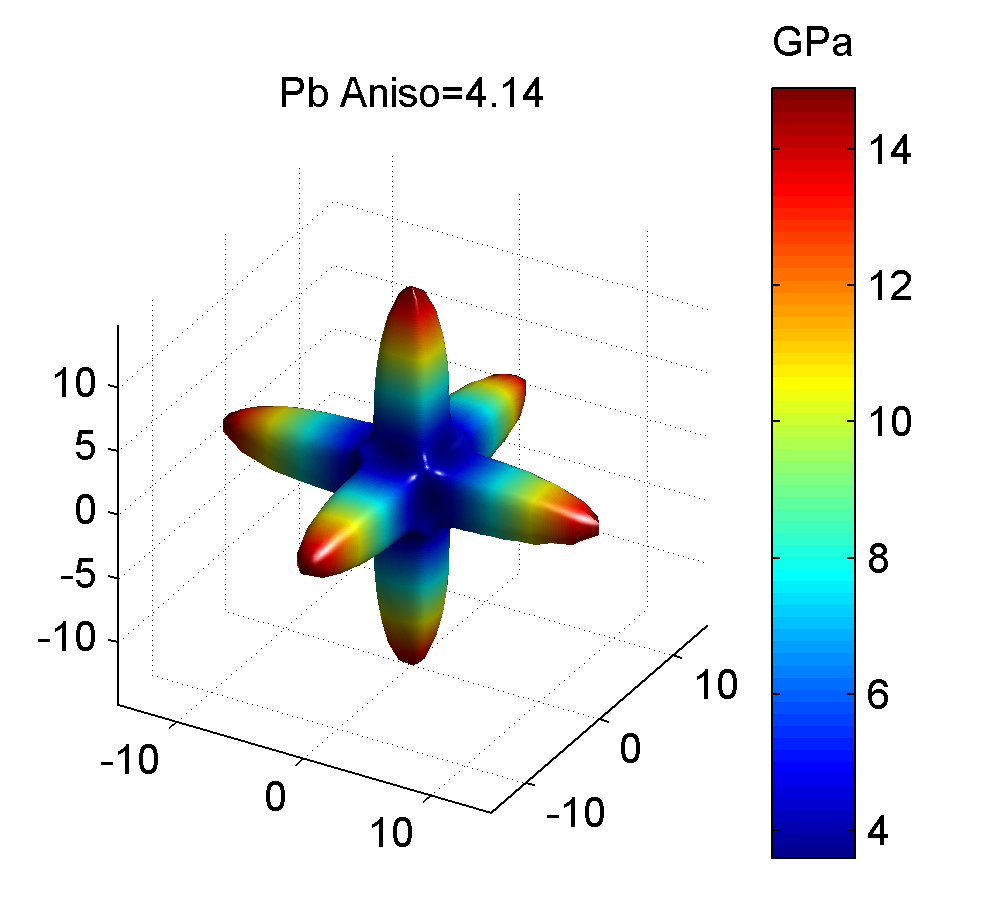
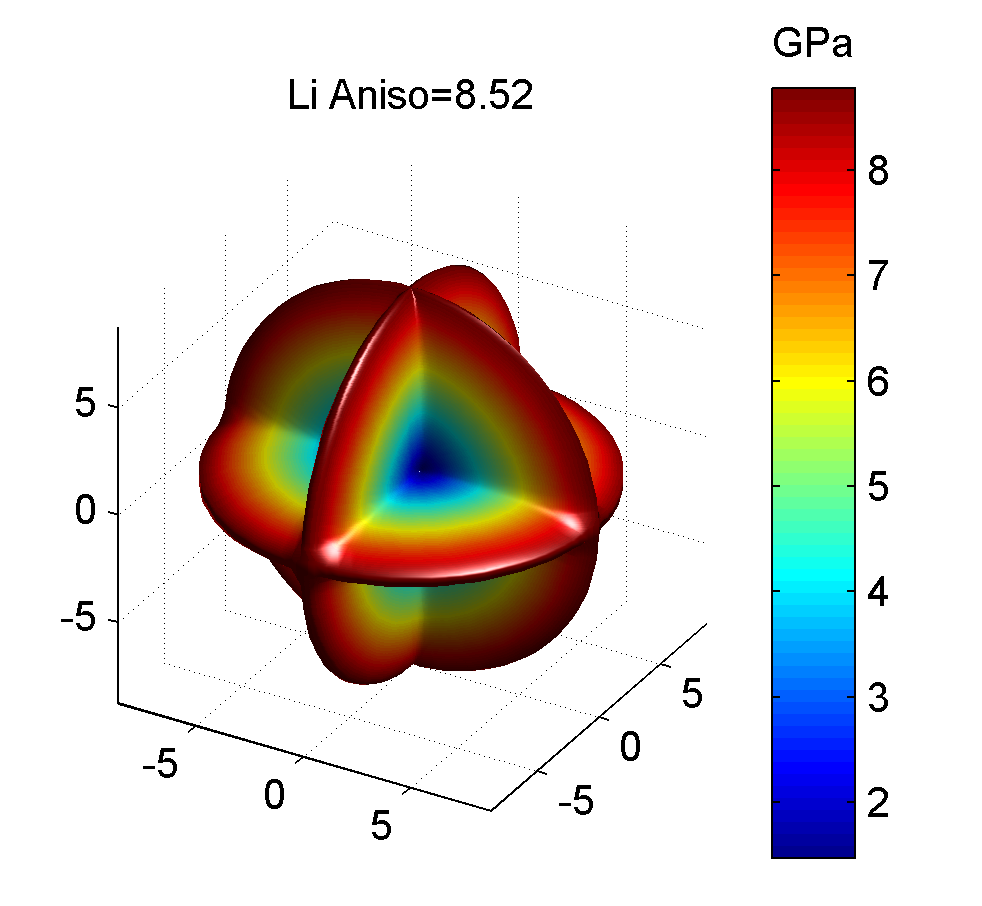
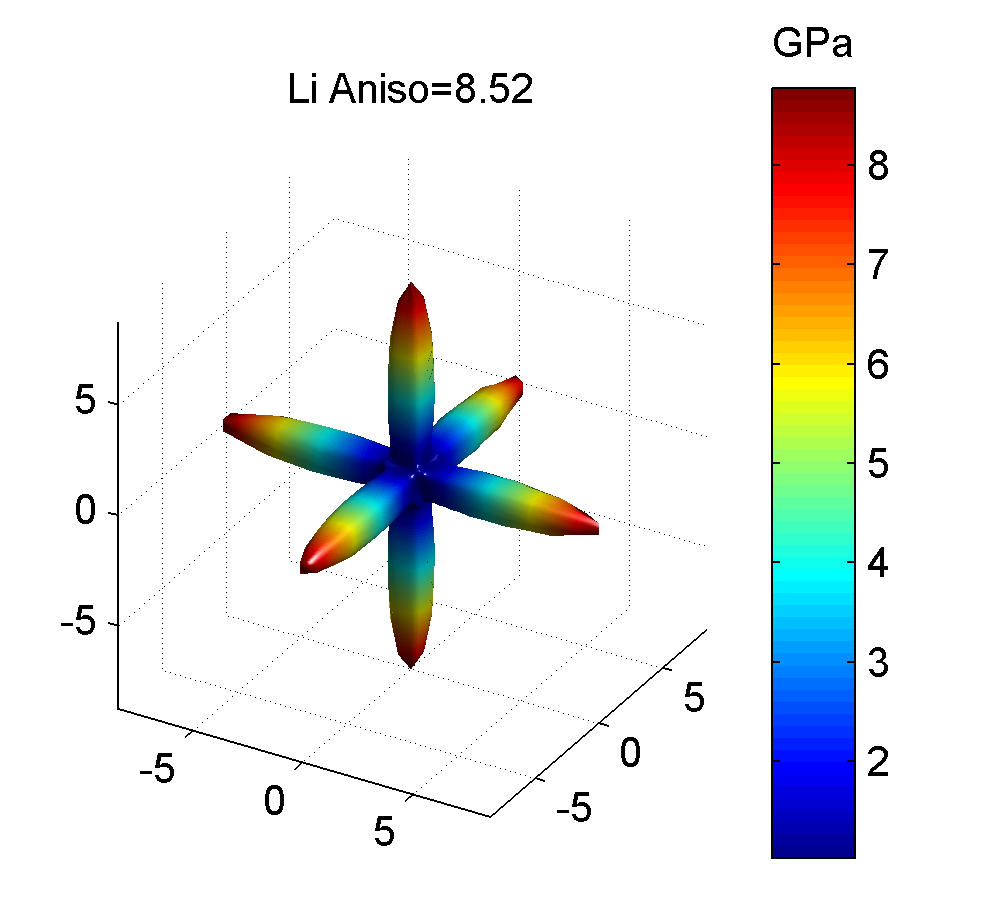
作图代码

剪切模量公式一致性

常值讨论

评论中有人指出, 在某些方向上剪切模量为常值, 这是可能的, 我给了一个简单的说明. 详细的讨论请参考下面两篇文章:

1. T. C. T. Ting; J Elasticity 81(3):271-292, 2006; 10.1007/s10659-005-9016-2
2. Kevin M. Knowles, Philip R. Howie; J Elast 120(1):87-108, 2014; 10.1007/s10659-014-9506-1

在线工具

本来我还打算做一个在线工具, 但是发现早就有人做好了, 所以还是作罢吧.

如果你需要对比, 可以使用ELATE: Elastic tensor analysis

评论

• 2015-04-01 16:52:10 棒棒 真是的太棒了

• 2015-04-01 20:06:30 Jerkwin 希望能提供更多信息.

• 2015-11-16 21:01:02 李润光 程序很棒，但为何（111）剪切面上不同方向剪切模量是定值？可否给出推导过程或出处？非常感谢！

• 2015-11-16 22:38:25 Jerkwin 不是很清楚你的问题, 请说得具体些.
• 2015-11-17 09:33:42 李润光 比如Fe是面心立方结构，最易开动的滑移系应该是（111）<-1 1 0>,但根据你的公式计算（111）面上沿任意方向滑移其剪切模量均是同一定值，从最大最小剪切模量图也可以看出，（111）面和（100）面上沿不同方向滑移的剪切模量都是定值，我认为这是不合理的，但没有找到相关的推导，可否请您解释一下。
• 2015-11-17 11:27:41 Jerkwin 如果我没理解错的话, 你把图的含义搞混了. 那些图给出的是某一方向上剪切模量的极值, 而不是同chi对应的剪切模量. 如果那样的话, 对每一方向, 都可以做出剪切模量和chi的关系图, 可能那是你想要的.
• 2015-11-17 12:17:40 李润光 我懂您的意思，图的含义我理解，是每个晶面上的模量极值。但仔细看一下，您的每一对图中，同种材料（111）面和（100）面上剪切模量的极大值和极小值均是相同的，我也用您的子程序画了这两个面上剪切模量和chi的关系图，是一条水平线，这是我困惑的地方，晶体学上，同一晶面沿不同剪切方向的模量不会是定值，我查找了相关文献，极少看到有关于此方面的推导，非常希望您给予进一步解释。
• 2015-11-17 13:02:20 Jerkwin 如果你说的(111)面对应的theta和phi都是PI/4的话, 执行主函数里面的[Gmin, Gmax] = pltGchi(.25pi, .25pi)语句会给出G和chi的关系图, 我得到的结果是正弦曲线, 不是直线, 和你说的不同.
• 2015-11-17 13:13:40 李润光 （111）面theta并非PI/4。按以下语句执行，

    Plane           = [1 1 1];
    pltGchi ( acos( Plane(3)./norm(Plane)), atan( Plane(2)./Plane(1)) );
  

  输出图形即为（111）面对不同chi的shear modulus，是一条直线。 Plane = [1 0 0]时也是直线。请您验证一下。
• 2015-11-17 14:40:38 Jerkwin 你说的对. 对这个特殊的方向, 剪切模量确实是常数. 原因如下: 根据最后的公式, 当G为常数时, 只需要满足Gmax=Gmin即可, 这样就可以得到C1=0并且C2=C3. 这两个等式也可以直接从G的第一个表达式看出来. 根据这两个条件就可以算出那些方向上的G为常数. 我粗略地算了一下,

    C1=-(alpha-beta) sin^2(tht) cos(tht) sin(4phi)/4
    C2-C3=(alpha-beta) sin^2(tht) { sin^2(tht) [ sin^2(2phi)-4 ] + cos(4phi)+3 }
  

  所以, 当alpha=beta时, G恒为常量. 除此之外, 在特定方向上G也可以为常量.其中的一个解就是你所说的(111)方向, 此时phi=PI/4, C1=0, cos^2(tht)=1/3, C2-C3=0, 满足等式. 当然, 根据这两个等式, 你还可以算出其他的方向, 我就没有验证了. 你有兴趣的话可以验算一下, 告诉我结果, 以便更新下上面的博文.
• 2015-11-18 17:29:36 李润光 恩，我想了下，（111）面模量为定值也是合理的。通常所说的最密排面最易滑移方向指实质上是指临界分切应力较小，势垒比较低。<1 -1 0>方向最易滑移并非因为模量小，而是原子间距小，平均伯氏矢量小，势垒低，这样看来你的计算在晶体学也是合理的。还是想看下原始推导过程，可能更有启发。
• 2015-11-18 23:45:34 Jerkwin 我不是研究晶体的, 所以晶体方面的知识不足. 希望你能把这个问题及其含义从晶体学方面论述一下, 我把数学部分补充上, 这样才好整理发布. 你写好后可以发到我的邮箱: Jerkwin@gmail.com.
• 2016-03-15 15:02:34 敦煌的木桶 下面这篇文章有推导，另外，对立方晶系而言，确实在(100)和(111)面上沿任意方向的剪切模量的值都是一样的。其他晶系的结果就不是这样的。 J Elast (2015) 120:87–108 Kevin M. Knowles · Philip R. Howie The Directional Dependence of Elastic Stiffness and Compliance Shear Coefficients and Shear Moduli in Cubic Materials

• 2016-03-17 06:02:36 Jerkwin 谢谢提供信息. 等我看过文章之后更新下博文.

• 2016-07-17 07:06:45 767676 必须点赞！良心好贴！

• 2016-07-25 16:04:52 Jerkwin 谢谢

• 2016-08-15 22:42:29 767676 本人在您的程序基础上，尝试做某切面轮廓，加代码如下：

    function SphPlt(X, Y, Z, F, File, Title)
        surf(X,Y,Z,F, 'FaceColor','interp', 'EdgeColor','none');
        hold on
       % 作模量的某一切面图
     [X,Y,Z]=meshgrid(linspace(-Gmax,Gmax));
     contourslice(X,Y,Z,X,x,y,z,[0 0])
        axis tight; title(Title);
        view(30,30); daspect([1 1 1]);
        camlight; lighting phong;
        cbar=colorbar; title(cbar, 'GPa');
  
        set(gca,'position',[0.12,0.05, 0.6,0.85]);
        set(gcf,'position',[500,500, 380,350]);
        set(gcf, 'PaperPositionMode', 'auto');
        print(gcf,'-dpng','-r300', File)
    end
  

  但是没有成功，敬请版主点播！

• 2016-08-16 23:51:27 Jerkwin 你要理解代码的含义. 你照抄的这几句放在这里不行, 因为大写的XYZ和小写的XYZ弄反了, 而且没有Gmax. 正确的差不多是这样

    hold on
    % 作模量的某一切面图
    [x,y,z]=meshgrid(linspace(-max(F(:)),max(F(:))));
    contourslice(x,y,z,x,X,Y,Z,[0 0])
  

• 2016-08-17 21:14:02 767676 多谢大神点拨！正如您所言，是我没有吃透代码含义，太心急了。敢问大神，能否给出您关于此段程序的引用文献。倘若有所小作，绝不敢忘引用您的原创。

• 2016-08-18 22:23:24 Jerkwin 如上所言, 我不是做材料的, 这些东西只不过是我业余帮人写的, 没有必要, 也不可能引用我的文献. 如果你真要引用相关文献的话, 引用上面ELAM的文献吧, 有些公式是我从它的源代码中抽出来的.

• 2016-08-17 17:40:47 斌 楼主可否提供立方外其它晶系的剪切模量的计算公式

• 2016-08-18 22:20:13 Jerkwin 公式我有, 但太复杂了, 还没有测试正确性. 由于我本人不是做材料的, 所以也没有这种需求. 如果你确实需要计算公式的话, 请参考我的另一篇博文那个程序的代码中有你需要的公式.

• 2016-10-27 12:37:45 好友昵称么 “此外, 与杨氏模量不同的是，剪切模量在某一方向 l 上的值还与角度 χ 有关. 这就导致剪切模量的各向异性比杨氏模量更加复杂。”我想请问下，上面这句话的角度 χ是怎么定义的

• 2016-10-27 21:31:06 Jerkwin 上面图中标出了χ 角, 仔细看下.

• 2017-03-12 21:49:50 流星 楼主其他晶系的剪切模量公式在哪有啊，能不能提供链接？

• 2017-03-13 11:07:58 Jerkwin 上面有人问了, 见我的回复.

• 2017-03-14 00:11:49 流星 请问下楼主，求不同晶面的比如（111）的剪切模量，要改代码的哪个部分啊？

• 2017-03-14 08:07:53 Jerkwin 不需要改什么, 使用Gchi函数就可以了
• 2017-03-14 19:10:52 流星 楼主大大，刚学matlab,对于脚本看的不是很懂，需要画个（111）面的切变模量，你说的用Gchi函数具体怎么操作啊？要是有时间，请指导下，谢谢！
• 2017-03-15 07:27:27 Jerkwin 给了theta和phi之后, 函数pltGchi(theta, phi)可以计算G和chi的关系, 并作图. 你试下就知道了.
• 2017-03-15 08:13:33 流星 对于（111）面的剪切模量，是不是二维的平面图啊？那知道theta和phi，在哪里调用pltGchi(theta,phi)函数啊，是在最后的function SphPlt（）里面吗，那原来的 surf(X,Y,Z,F, 'FaceColor','interp', 'EdgeColor','none');是不是用#注释掉啊？哈哈，问题有点多，脑袋不灵光，希望楼主能回答。嗯，楼主大才，赞！！
• 2017-03-15 09:44:26 Jerkwin 基本语法你都不明白的话, 我说了也是白白浪费时间. 你先去看看matlab的基础再说.
• 2017-03-15 12:09:57 流星 好的 ，还是多谢大神啦