
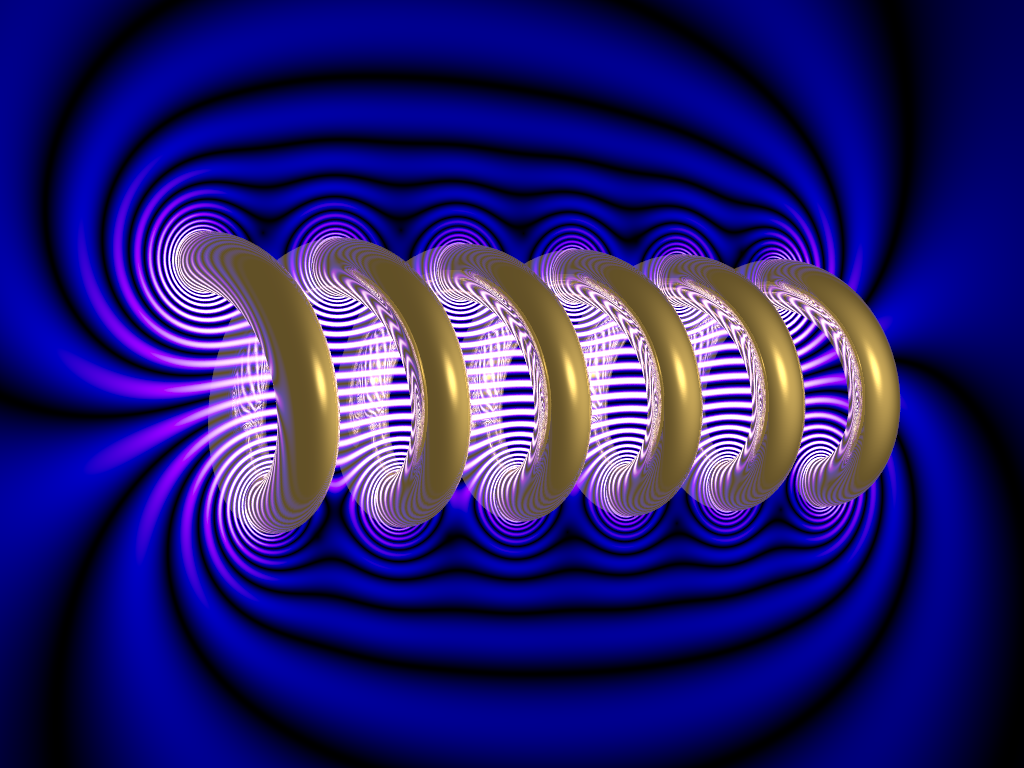
Paul Nylander使用POV-Ray渲染了很多漂亮的图片, 其中有一个单层螺线管周围磁场的示例, 并给出了代码.

但我直接运行代码后得到的图像与他给出的图像存在不少差距. 为此, 我向他询问了一下原因, 才知道他并没有直接渲染金属线圈, 而使用了环境贴图. 可惜的是他不愿将其分享出来, 因为要保留他的艺术特色. 这样的话, 我们只能自己来发挥了.
他所给的示例代码并不易理解, 且其中的好多数字都是直接写死的, 是magic number, 让人不解. 我自己研究了一下才明白, 他这段代码, 在计算磁感强度时采用的是一个很粗糙的近似: 只考虑导线与截面相交的接触点, 且将其视为无限长载流导线, 截面内任一点的磁感强度就是这些接触点所产生磁场强度的矢量叠加. 这样的话, 计算简单了许多, 但相应的结果并不准确, 虽然作为示意图是足够了.
弄明白了原理以后, 我将原先的代码进行了整理, 且添加了注释, 方便理解与修改. 这个代码给出的图像如下, 虽然没有原始的漂亮, 但尚可接受.
下面我们来做一些更精细的计算. 理论上, 单层螺线管周围的磁场分布是存在闭式解的, 但涉及椭圆函数, 并不易计算. 所以, 我们还是直接使用数值积分计算吧. 将螺线管的电流划分为很多段, 每段视为直线, 做数值积分就可以求得磁感强度了.
设以 $\q$ 为参数的螺旋线方程为
$$\alg x &= R \cos\q \ y &= R \sin\q \ z &= b\q={h \over 2\pi} \q \ealg$$
其中 $R$ 为螺线管半径, $h$ 为螺距, 弧长
$$l(\q)=\int_0^\q \sqrt{x'(\q)^2+y'(\q)^2+z'(\q)^2} d\q=\sqrt{R^2+b^2}\q$$
螺旋线上一点 $\bi r_i$ 处的弧长微元
$$\rmd {\bi l_i}=\Bmat x'(\q) \ y'(\q) \cr z'(\q) \eBmat = \Bmat -R\sin\q \ R\cos\q \ b \eBmat=\Bmat -y_i \ x_i \ b \eBmat$$
根据Biot–Savart定律, 空间一点 $\bi r$ 处的磁感强度为
$$\alg
\bi B &={\m_0 I \over 4\p } \int {\rmd {\bi l} \times (\bi r-\bi r_i) \over r^3} \
&={\m_0 I \over 4\p } \Bmat
\int {x_i(z-z_i)-b(y-y_i) \over r^3} \
\int {y_i(z-z_i)+b(x-x_i) \over r^3} \
\int {-y_i(y-y_i)-x_i(x-x_i) \over r^3}
\eBmat \
&={\m_0 I \over 4\p } \Bmat
\Sum_i {x_i(z-z_i)-b(y-y_i) \over r^3} \
\Sum_i {y_i(z-z_i)+b(x-x_i) \over r^3} \
\Sum_i {-y_i(y-y_i)-x_i(x-x_i) \over r^3}
\eBmat \
\ealg$$
使用这种方法得到的图如下

和前面的图相比, 基本看不出差别.
如果我们直接作出截面图, 应该是这样
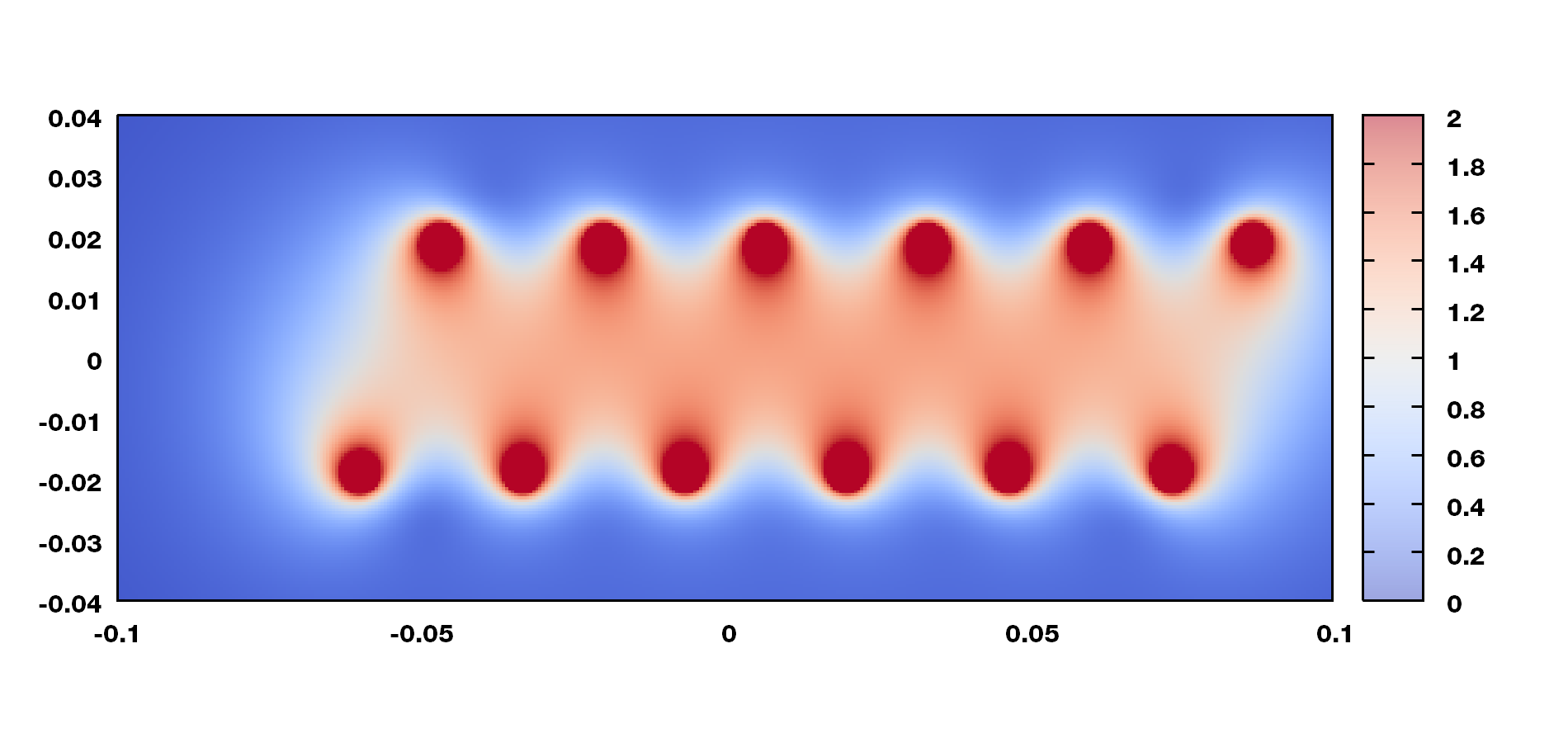
此外, 在作图时, 使用相对强度更好一些, 下面是一些特殊体系的磁感强度, 可用于确定相对强度.
如果你熟悉matlab, 可以参考下面的资料: