仓库源文，站点原文

layout: post title: 圆球堆积接触数的估算 categories:

• 科 tags:
• 数理 math: true

• 2022-03-23 15:01:45 整理: 张嘉兴; 修订: 李继存

问题

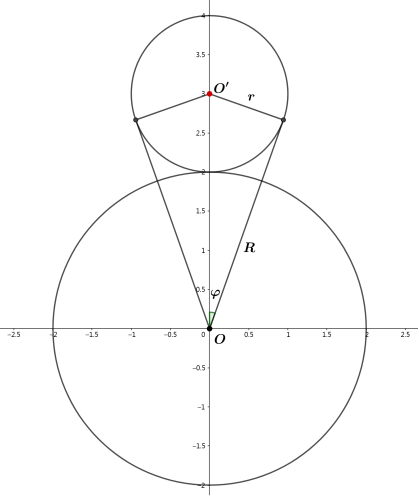
有刚性球, 大球半径为$R$, 小球半径为$r$, 每个小球都与大球紧密接触, 问大球周围最多可以放置的小球数$N$.

这是空间堆积中的一个经典问题, 据我所知, 至今还没有完全解决, 只有一些已知解和上下限的估计结果. 对于$r=R$的特殊情况, $N=12$, 是个著名的结果, 也有称为牛顿数的.

这个问题的答案在分子建模方面的应用主要是构建一些特殊结构时确定所需的分子数目, 如囊泡, 纳米颗粒等. 当然, 这还需要知道分子的最小直径或动力学直径, 不过这是另一个问题了.

二维情况

与问题对应的二维情况, 我们很容易根据每个小圆遮蔽的大圆的圆心角计算.

$$╤ N &={2π／2φ}={π／\arcsin{r／R+r} } \ &={π／\arcsin{ρ／1+ρ} }, □ρ=r/R ╧$$

当$ρ=1$时, $N={π／\arcsin{1／2} }=6$, 符合我们熟知的结果.

三维上限解

将二维问题的求解方法推广到三维, 平面圆心角对应球的立体角, 整个大球的立体角为$4π$(我们忽略其单位), 所以只要算出每个小球所遮蔽的立体角, 即可得到大球周围紧密接触的小球数. 这个数字是上限, 因为不同于二维情形, 即便所有小球彼此之间都紧密接触, 所有小球遮蔽的立体角也不能覆盖整个球面, 因为小球之间会留有空隙, 每3个小球之间会留出一个曲边三角区域. 如果不考虑这些小的曲边三角区域, 得到的接触数就是上限值. 我们先算一下这种简单的情况.

被小球遮蔽的部分在大球上是一个球冠, 做剖面如下图,

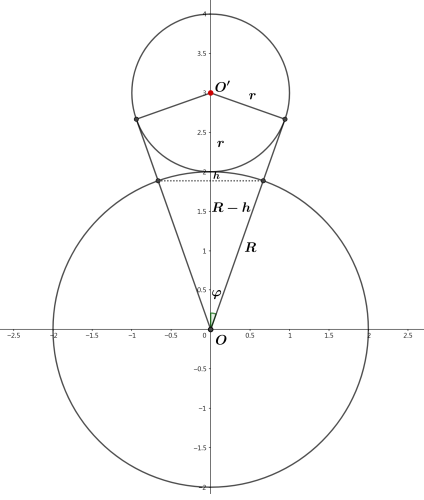
根据几何关系

$$╤ \sinφ&={r／R+r}={ρ／1+ρ} \ \cosφ&=√{1-\sin^2φ}={√{1+2ρ}／1+ρ}=κ ╧$$

球冠高

$$h=R-R\cosφ=R(1-κ)=R（1-{√{1+2ρ}／1+ρ}）$$

球冠表面积

$$A₀=2πRh=2πR^2（1-κ）$$

球冠对应的立体角

$$Ω₀={A₀／R^2}=2π（1-κ）$$

最终接触数

$$N₀ ={4π／Ω₀}={2／1-κ}, □ κ={√{1+2ρ}／1+ρ}, \, ρ={r／R}$$

若$ρ=1$, 则$N₀={2 ／ 1-{√3／2} }≈14.928$. 与准确值$12$相比, 可见, 小球之间的空隙最好不要简单地忽略.

这里多说一句, 利用体积关系而不是立体角关系, 也可以解, 我们在这里就不考虑这种方法了, 感兴趣的可以试试.

此外, 计算球冠表面积时也可使用重积分的方法, 稍麻烦一些.

三维空隙解

现在我们来考虑那些曲边三角区域, 计算出它们在球面上的面积, 从而得到对应的立体角. 这是一个立体几何问题, 并涉及球面几何. 这类问题一般可以采用两种方式解决: 解析几何方式, 建立坐标系, 借助向量等进行代数运算; 纯几何方式, 不考虑坐标, 只考虑边角等几何元素. 显然, 对某个具体的问题, 两种解决方式给出的结果应该且必须一致, 只不过求解过程的复杂程度可能不同. 此外, 计算出的解析结果也应该与数值计算结果吻合. 对于某些答案未知的问题, 解决方法越多越好, 这样不同方法得到的结果才能交叉验证. 真实正确的结果无论从哪个角度看都是正确的, 而虚假的结果只能在特定条件下表现出真实. 科学史上这类故事很多. 好像是玻尔曾经说过吧, 一个概念至少要用两种语言思考过, 一个结果至少能从两种理论得到, 才算合格.

这个问题的三维示意如下

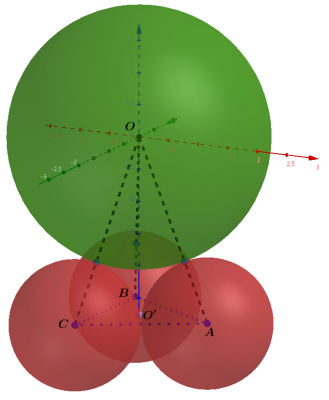
设三个小球分别为球$A$, $B$, $C$, 大球球心记为$O$. 我们建立直角坐标系, 坐标原点位于大球球心$O$, 三个小球位于$xOy$平面下, 球$A$位于正$x$轴上, 球$B$和$C$位于负$x$轴一侧, 且关于$xOz$平面对称, 三个小球的球心所成正三角形的中心$O'$位于负$z$轴, 坐标为$(0,0,-h)$. 以三个小球球心所在平面为剖面图如下

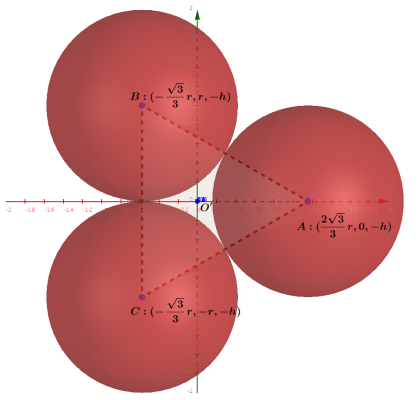
容易知道, 各球心坐标为

$$ ╤ &A: ({2√3／3}r, 0, -h) \ &B: (-{√3／3}r, r, -h) \ &C: (-{√3／3}r, -r, -h) ╧$$

四个球心$O-ABC$成正三角锥, 锥高$h$为大球球心$O$到小球球心所在平面的距离(即$OO'$的长度), 如下图所示

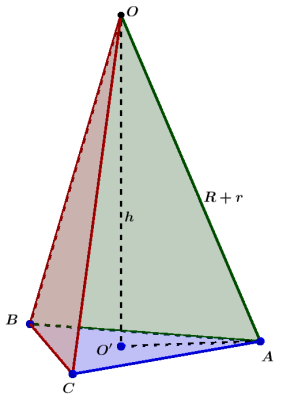
我们有

$$╤ (R+r)^2&=h^2+O'A^2=h^2+(2√3r/3)^2 \ h&=√{(R+r)^2-{4／3}r^2}={√3／3}√{3R^2+6Rr-r^2} \ &={√3／3}R√{3+6ρ-ρ^2} ╧$$

定义面积$A₁$为大球被三角锥$O-ABC$所截等曲边三角区域的面积, $A₀$为大球被圆锥$OA$所截球冠的表面积. 三维图不由于互相遮蔽, 不容易看明白的话, 也可以将三个小球等效为一定半径的圆, 三个圆切除球面后剩余部分的面积就是我们要求的. 下面是从不同方向查看时的示意图.

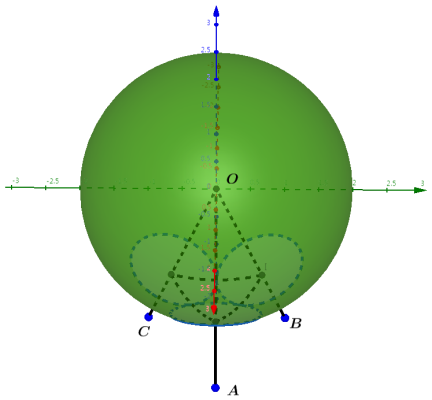
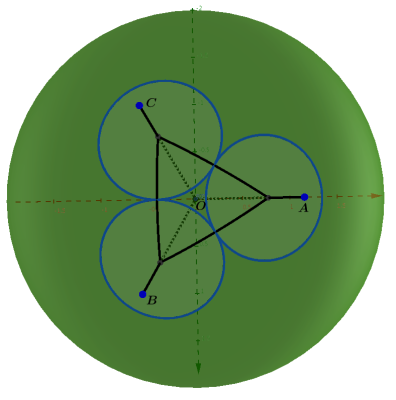
假 定 每 个 小 球 都 与 周 围 6 个 其 他 小 球 紧 密 接 触, 容易知道, 要求曲边三角形面积

$$A=A₁-3×{A₀／6}=A₁-½A₀$$

$A₀$前面已经算过, 所以只剩下曲边三角区域的面积要算.

由于曲边三角区域的三条边都是大球的大圆, 所以这个曲边三角区域为球面三角形, 根据球面三角形面积公式,

$$A₁=(θ₁+θ₂+θ₃-π)R^2$$

其中$θ_i$为球面三角形的球面角. 对我们要处理的情况, 球面三角形的三个球面角大小相等, 设为$θ$, 因此$A₁=(3θ-π)R^2$.

不难发现$θ$为正三角锥$O-ABC$任意两个侧面所成的二面角, 例如平面$OAB$与平面$OBC$的夹角. 下面我们用解析几何坐标法和纯几何方法分别计算这个角度, 以求互相验证, 确保正确.

计算球面角

先使用坐标法. 为此我们需要分别计算平面$OAB$的法向量

$$\vec n₁=\vec{BO}×\vec{BA}=({√3／3}r, -r, -h)×(√3r, -r, 0)=r(h, √3h,{2√3／3}r)$$

以及平面$OBC$的法向量

$$\vec n₂=\vec{BO}×\vec{BC}=({√3／3}r, -r, -h)×(0, -2r, 0)=2r(h, 0, -{√3／3}r)$$

从而两平面所成二面角$θ$的余弦值为

$$╤ \cosθ&={\vec n₁·\vec n₂ ／|\vec n₁| |\vec n₂|} \ &={r(h, √3h,{2√3／3}r)·2r(h, 0, -{√3／3}r) ／√{r^2(h^2+3h^2+4r^2/3)}√{4r^2(h^2+r^2/3)} } \ &=½{3h^2-2r^2／3h^2+r^2} \ &=½（1-{3r^2／3h^2+r^2}） \ &=½（1-{3r^2／3(R+r)^2-4r^2+r^2}） \ &=½（1-{r^2／R^2+2Rr}）\ &=½（1-{ρ^2／1+2ρ}） ╧$$

若使用几何法, 则如下图, 作$AD \perp OB$, 则$CD \perp OB$, 且$CD=AD$, $∠ADC$即为所求.

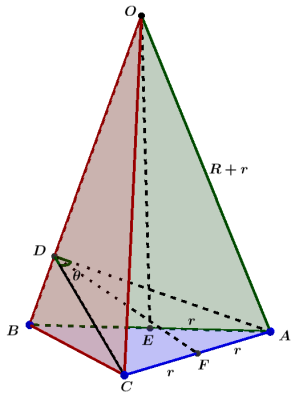
取$AB$中点$E$, $AC$中点$F$, 则$DF \perp AC$, $OE \perp AB$, 有

$$\sin{θ／2}={r／AD}$$

根据三角形$OAB$面积相等

$$╤ AD × OB=AB × OE \ (R+r) AD=2r√{(R+r)^2-r^2} \ AD={2r√{(R+r)^2-r^2} ／R+r}={2r√{R^2+2Rr} ／R+r} ╧$$

故

$$╤ \sin{θ／2}&={r／AD}= {R+r ／2√{R^2+2Rr} }={1+ρ ／2√{1+2ρ} }={1／2κ} \ \cosθ&=1-2\sin^2{θ／2}=1-½{(1+ρ)^2 ／1+2ρ}=½（1-{ρ^2／1+2ρ}）=1-{1／2κ^2} ╧$$

所得结果与坐标法相同. 由于是正三角锥所以使用几何法计算也不太麻烦.

因此, 我们得到曲边三角区域面积

$$╤ A&=A₁-½A₀ \ &=R^2(3θ-π)-½2πR^2(1-κ) \ &=R^2(3θ+κπ-2π), □κ={√{1+2ρ}／1+ρ}, \, ρ={r／R} ╧$$

对于此面积公式, 我们可以考虑下极限情况. 若小球半径$r$取固定值, 而大球半径$R$趋向于无穷大, 则大球球面趋近于平面, 所得面积趋近于平面上三个小圆所围成的曲边三角形面积$(√3-{π／2})r^2$. 此面积值应当可以从上述公式的极限推出, 但我能力有限, 未能得到.

相应的立体角

$$╤ Ω&={A／R^2} \ &=3θ+κπ-2π \ &=6\arcsin{1／2κ}+(κ-2)π, □κ={√{1+2ρ}／1+ρ}, \, ρ={r／R} ╧$$

接触数

由此, 我们最终得到假定条件下的接触数

$$╤ N&={4π／Ω₀+6Ω/3} \ &={2π／π(1-κ)+6\arcsin{1／2κ}+(κ-2)π} \ &={2π／6\arcsin{1／2κ}-π}, □κ={√{1+2ρ}／1+ρ}, \, ρ={r／R} ╧$$

若$ρ=1$, 则$κ={√3／2}$, 接触数

$$N={2π／6\arcsin{√3／3} -π}≈11.397$$

与准确值$12$相比, 过小.

至此, 这个问题露出其狰狞的一面. 在等径堆积情况下我们之所以得到小于12的结果, 其原因在于所做的假定不能成立. 根据拓扑学, 球面是没有办法使用全等六边形划分的, 无论半径比如何, 都不可能出现每个小球都与周围6个其他小球紧密接触情况, 必定会出现其他多边形, 如五边形, 想想足球, 对任意半径比, 是没法保证每个小球周围都有6个其他小球紧密接触的, 半径比不同, 平均接触的小球数目也不同, 因此, 我 猜 想 上 面 得 到 的 值 是 下 限, 且 半 径 比 越 大, 此 下 限 值 越 接 近 实 际 值. 如果猜想是对的, 那我们得到的接触数

$${2π／6\arcsin{1／2κ}-π} < N < {2／1-κ}, □ κ={√{1+2ρ}／1+ρ}, \, ρ={r／R}$$

对等径堆积, 接触数的范围为12到14, 这或许可以解释, 历史上曾有人认为等径堆积的接触数为13.

等径最密堆积

对等径圆球最密堆积的情况, 仔细观察一下其结构(红: 曲边三角区域; 蓝; 曲边四角区域),

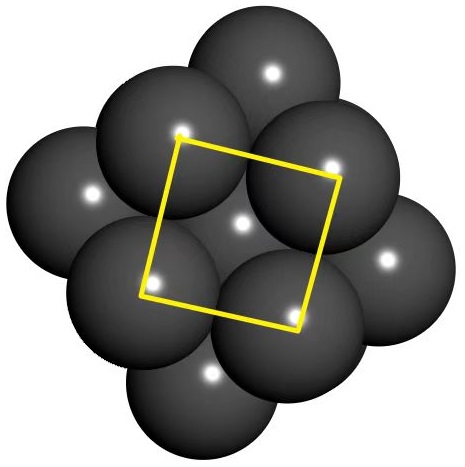
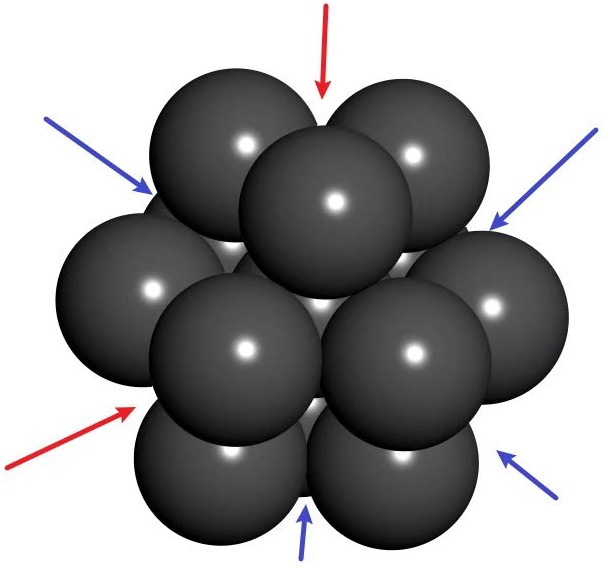
会发现, 12个小球形成8个曲边三角区域, 其他为曲边四角区域. 理论上, 中心球的表面积应该等于12个小球对应的球冠表面积, 8个球面三角形, 6个球面正方形面积之和. 在等径情况下一个小球周围完全不可能有6个紧密接触的小球. 如果要更仔细地考虑这一点, 先要考虑半径比取何值时, 一个小球周围才可能有6个紧密接触的小球, 接下来可以考虑曲边四角区域立体角的计算. 这些计算于我而言, 太多精细, 也过于困难, 所以就此打住吧.

如果我们使用外接球面三角形的面积进行估计, 即做三个紧密接触小球的外接三角锥, 它会在大球上截出一个大的球面三角形,

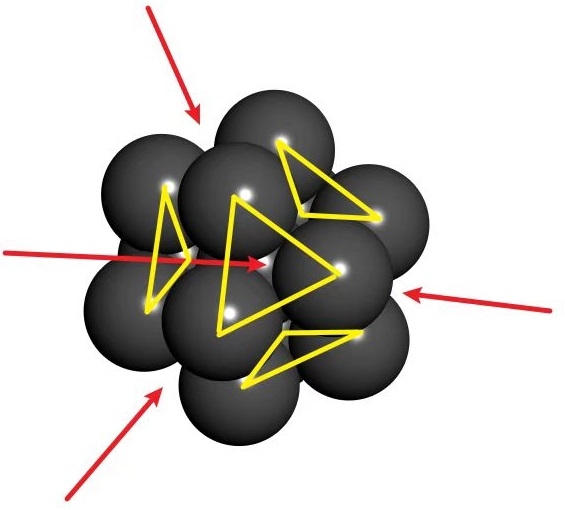
使用和前面类似的方法, 我们可以计算出这个大的球面三角形的面积. 这样的大三角形总共4个, 每个由3个小球组成, 根据三角形的面积可以计算出最多容纳$4.862$个三角形, 也就是$14.586$个小球, 比基于球冠面积的结果$14.928$稍小一些.

验证四面体立体角的其他公式

下面我们使用另外的方法来验证前面所得的四面体对应的立体角.

$$\def\tg{\text{tg} } \def\ctg{\text{ctg} }$$

四面体$O-ABC$对应立体角的计算公式有很多, 维基百科给出了其中两个, 一个是计算1/4角度正切的L'Huilier定理, 基于几何量:

$$\tg{Ω／4}=√{\tg {s／2} \tg {s-α／2} \tg {s-β／2} \tg {s-γ／2} }$$

其中$α=∠BOC, β=∠AOC, γ=∠AOB, s={α+β+γ／2}$

对我们要处理的情况, $α=β=γ=θ, s={3θ／2}$, 所以

$$\tg{Ω／4}=\tg {θ／4}√{ \tg {θ／4} \tg {3θ／4} }$$

再结合正切三倍角公式

$$\tg 3x={\tg^3 x-3\tg x／3\tg^2 x-1}=\tg x\tg（{π／3}+x）\tg（{π／3}-x）$$

或许可以证明得到的结果与前面的一致, 但我能力有限, 无法证明.

另一个计算四面体立体角的公式使用了半角的正切和向量的各种积, 适用于解析几何情况, 在实际中可能更方便, 也更精确:

$$\tg{Ω／2}={|\vec a\; \vec b\; \vec c| ／abc+(\vec a·\vec b)c +(\vec a·\vec c)b+(\vec b·\vec c)a}$$

对我们的情况, $\vec a, \vec b, \vec c$三个向量长度均为$R+r$, 且彼此间的夹角$α$也相等, 所以可以化简上式为

$$\tg{Ω／2}={\vec a ·(\vec b × \vec c) ／abc(1+3\cosα)}$$

根据余弦定理

$$╤ \cos α&= {2(R+r)^2-(2r)^2／2 (R+r)^2}=1-{2r^2／(R+r)^2} =1- {2ρ^2／(1+ρ)^2} \ 1+3\cos α&=4-{6ρ^2／(1+ρ)^2}=2{2+4ρ-ρ^2／(1+ρ)^2} ╧$$

我们先用坐标法来计算向量的三重积, 根据球心坐标

$$╤ & A: ({2√3／3}r, 0, -h) \ & B: (-{√3／3}r, r, -h) \ & C: (-{√3／3}r, -r, -h) ╧$$

可得三重积

$$╤ \vec a ·(\vec b × \vec c)&=「 {2√3／3}r & 0 & -h \ -{√3／3}r & r & -h \ -{√3／3}r & -r & -h」\ &=2√3 r^2h \ &=2√3 r^2 {√3／3}R√{3+6ρ-ρ^2} \ &=2r^2R√{3+6ρ-ρ^2} ╧$$

从而

$$╤ \tg{Ω／2}&={ 2r^2R√{3+6ρ-ρ^2}／ (R+r)^3(1+3\cosα)} \ &={2ρ^2√{3+6ρ-ρ^2}／(1+ρ)^3 (1+3\cosα)} \ &={2ρ^2√{3+6ρ-ρ^2}／(1+ρ)^3 2 {2+4ρ-ρ^2／(1+ρ)^2} } \ &={ρ^2／1+ρ} {√{3+6ρ-ρ^2} ／ 2+4ρ-ρ^2} ╧$$

如果我们不借助坐标, 而使用几何方法计算三重积, 则有

$$╤ \vec a ·(\vec b × \vec c) &=a^3 \cosφ\sinα \ \tg{Ω／2}&={\vec a ·(\vec b × \vec c) ／a^3(1+3\cosα)} \ &={\cosφ\sinα ／(1+3\cosα)} ╧$$

其中$φ$为平面$OBC$的法向量$\hat n$与$OA$之间的夹角, 如下图

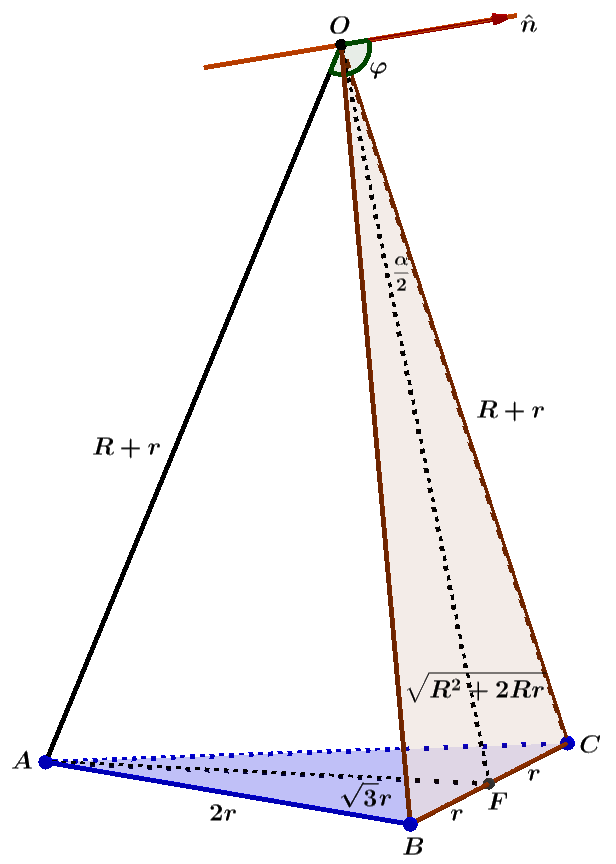
根据几何关系, 有

$$╤ \sin{α／2}&={r／R+r}={ρ／1+ρ} \ \cos{α／2}&={√{1+2ρ}／1+ρ} \ \tg{α／2}&={ρ／√{1+2ρ} } \ \sin α&=2\sin{α／2}\cos{α／2}={2ρ√{1+2ρ}／(1+ρ)^2} \ \cosα&=1-2\sin^2{α／2}=1-2{ρ^2／(1+ρ)^2}={1+2ρ-ρ^2 ／(1+ρ)^2} \ 1+3\cosα&=1+3 {1+2ρ-ρ^2 ／(1+ρ)^2} = 2{2+4ρ-ρ^2／(1+ρ)^2} ╧$$

由于$\hat n \perp OBC$, 所以$\hat n \perp OF$, 且$\hat n$, $OA$, $OF$三者共面, 从而

$$╤ \cos(φ-{π／2})&=\sin φ \ &= {(R+r)^2+R^2+2Rr-3r^2／2(R+r)√{R^2+2Rr} } \ &= {R^2+2Rr-r^2／(R+r)√{R^2+2Rr} } \ &={1+2ρ-ρ^2／(1+ρ)√{1+2ρ} } \ \cos φ&=√{1-\sin^2 φ} \ &= {√{(1+ρ)^2 (1+2ρ)-(1+2ρ-ρ^2)^2}／(1+ρ)√{1+2ρ} } \ &={ρ／1+ρ} {√{3+6ρ-ρ^2}／√{1+2ρ} } ╧$$

因此,

$$╤ \tg{Ω／2}&={\cosφ\sinα ／1+3\cosα} \ &={ρ／1+ρ} {√{3+6ρ-ρ^2}／√{1+2ρ} } {2ρ√{1+2ρ}／(1+ρ)^2} {(1+ρ)^2／ 2(2+4ρ-ρ^2)} \ &={ρ^2／1+ρ} {√{3+6ρ-ρ^2}／2+4ρ-ρ^2} \ ╧$$

与坐标法所得结果一致.

下面我们看看前面得到的球面角是否与此一致. 根据前面的结果

$$╤ Ω &=3θ-π \ \sin{θ／2} &={1／2κ}={1+ρ／2√{1+2ρ} } \ \tg{θ／2}&={1+ρ／√{3+6ρ-ρ^2} } \ \ctg{θ／2}&={√{3+6ρ-ρ^2}／1+ρ} ╧$$

根据三倍角公式,

$$╤ \ctg{3θ／2}&={\ctg^3{θ／2}-3\ctg{θ／2}／3\ctg^2{θ／2}-1} \ &=\ctg{θ／2} {\ctg^2{θ／2}-3／3\ctg^2{θ／2}-1} \ &=\ctg{θ／2} { {3+6ρ-ρ^2／(1+ρ)^2}-3 ／3{3+6ρ-ρ^2／(1+ρ)^2}-1} \ &=\ctg{θ／2} {-ρ^2／2+4ρ-ρ^2} \ &=-{ρ^2／1+ρ}{√{3+6ρ-ρ^2}／ρ^2-4ρ-2} ╧$$

最终可以得到

$$╤ \tg{Ω／2} &=\tg（{3θ／2}-{π／2}）\ &=-\tg（{π／2}-{3θ／2}）\ &=-\ctg{3θ／2} \ &={ρ^2／1+ρ}{√{3+6ρ-ρ^2}／ρ^2-4ρ-2} ╧$$

与前面的结果一致.

与数值方法的结果对照

根据前面的示意图, 我们可以构建一个大球, 三个小球的体系, 设定它们的具体半径值, 然后使用数值方法计算曲边三角区域的面积, 所得结果应该与我们的结果一致.

有很多程序可以计算重叠球体的表面积与体积, 我曾使用过一个程序见ARVO: A Fortran package for computing the solvent accessible surface area and the excluded volume of overlapping spheres via analytic equations.

由于我对上面所得的结果过于自信, 所以就不再进行验证了.

与已有值的比较

这个问题实际上是球面编码问题Spherical Code, 或Toth问题. N. J. A. Sloane收集了很多已知结果, 对于三维, 有$N<=130$的结果, 我在这里整理一下.

题外话

对一些未知的问题, 我们有时并不能确定自己最终能得到什么. 幸运的话, 或许能得到一点有用的答案. 而更多时候, 最终留给我们的, 只是思考自身. 在科学研究中, 这才是常态. 我有时甚至觉得, 那些斩钉截铁的答案, 那些不可置否的回答, 虽然似乎消弭了不确定性, 让人暂时心安, 但其本身是反科学的. 科学并非纯粹的真理, 也不是真理自身, 而只是追求真理的过程. 虽然, 科学连真理的存在性都无法证明.

这正如旅行, 我们不要单单关心目的地, 也要学着欣赏沿途的风景. 这欣赏自身就是另一种旅行.

人生亦如是. 我们只是生命中的行者, 便如是走着, 天地之间, 走得或快或慢, 目的或有或无, 终归都是一场没有归期的远行.