在论文 Marco Bernardi, Maurizia Palummo, Jeffrey C. Grossman; Semiconducting Monolayer Materials as a Tunable Platform for Excitonic Solar Cells; ACS Nano 6(11):10082-10089, 2012; 10.1021/nn303815z 中讨论了一种计算太阳能电池效率的方法, 并给出了效率与材料参数的关系图, 对研究太阳能电池的人有一定参考价值. 我这里给出文章中计算太阳能电池效率的matlab代码, 供需要的人参考. 由于我的专业并非此领域, 所以无法对公式含义及其中的各个物理量进行说明, 只关注公式的数学部分.
理论
首先指出, 论文中的太阳能电池效率计算公式(方程1)有误, 正确的公式如下
$$\h={0.65(E_g^{opt,d}-\D Ec-0.3) \int{Eg^{opt,d}}^\infty {J{ph}(\hbar \w)\over \hbar \w} \rmd (\hbar \w) \over \int0^\infty J{ph}(\hbar \w) \rmd (\hbar \w) }$$
与原公式的区别在于分母中积分的起点为能量的起始值.
由于 $\hbar\w=\ve$ 即为光子的能量, 所以上式可写为
$$\h={0.65(E_g^{opt,d}-\D Ec-0.3) \int{Eg^{opt,d}}^\infty {J{ph}(\ve)\over \ve} \rmd \ve \over \int0^\infty J{ph}(\ve) \rmd \ve }$$
此式的分母部分是一个常数, 无须考虑, 故此, 计算的关键是分子中的积分. 此积分的计算涉及标准太阳能光谱 $J_{ph}(\w)$. 根据国际标准, 此光谱一般采用美国材料和试验协会(ASTM)的标准太阳能光谱(ASTM)G173-03, 但此光谱给出的数据是按波长分布的, 所以我们首先需要将其转换为按能量分布的光谱.
设有光谱的波长分布为 $f(\l)$, 其对应的能量分布为 $J(\ve)$, 二者满足 $f(\l) \rmd \l =J(\ve) \rmd \ve$, 故
$$J(\ve) = f(\l) \abs{ {\rmd \l \over \rmd \ve} } = f(\l) { 1\over \abs{\rmd \ve /\rmd \l} }$$
由
$$\ve=h\n=h{c\over \l}, \rmd \ve=-{hc\over\l^2} \rmd \l$$
可得
$$J(\ve)={\l^2 \over hc} f(\l)={\l \over \ve} f(\l)$$
知道了此式之后, 使用最简单的梯形法对能量分布进行积分即可. 需要注意的是, 积分时可能需要首先对数据进行线性插值, 因为积分的起点可能并不正好处于分布的点上.
代码
<table class="highlighttable"><th colspan="2">matlab</th><tr><td><div class="linenodiv" style="background-color: #f0f0f0; padding-right: 10px"><pre style="line-height: 125%"> 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50</pre></div></td><td class="code"><div class="highlight" style="background: #f8f8f8"><pre style="line-height: 125%">clc; clear; clear all;
<span style="color: #008800; font-style: italic">% 单位换算</span>
nm2eV=<span style="color: #666666">1.2398419739e-6*1e9</span>;
<span style="color: #008800; font-style: italic">%% 处理数据</span>
<span style="color: #008800; font-style: italic">% 读取文件, 忽略表头, 使用Global tilt数据</span>
dat = csvread(<span style="color: #BB4444">'</span>ASTMG173.csv<span style="color: #666666">'</span>,<span style="color: #666666">2</span>);
l=dat(:,<span style="color: #666666">1</span>); f=dat(:,<span style="color: #666666">3</span>);
<span style="color: #008800; font-style: italic">% 由波长分布换算为能量分布, 递增顺序</span>
E=nm2eV<span style="color: #666666">./</span><span style="color: #AA22FF">flipud</span>(l);
J=<span style="color: #AA22FF">flipud</span>(f<span style="color: #666666">.*</span>l)<span style="color: #666666">./</span>E;
<span style="color: #008800; font-style: italic">% plot(E,J,'-')</span>
<span style="color: #008800; font-style: italic">% 计算能量最小点与最大点, 能量间隔最小值</span>
<span style="color: #008800; font-style: italic">% 梯形法积分得总功率, 其值应接近1000</span>
Emin=min(E); Emax=max(E);
dEmin=min(gradient(E));
Jtot=trapz(E, J)
<span style="color: #008800; font-style: italic">%% 计算单个效率值</span>
Eopt=<span style="color: #666666">2</span>; Ec=<span style="color: #666666">0.2</span>;
Eintp=[Eopt:dEmin:Emax];
Jintp=interp1(E,J, Eintp, <span style="color: #BB4444">'</span>linear<span style="color: #666666">'</span>);
Jsc=trapz(Eintp, Jintp<span style="color: #666666">./</span>Eintp)<span style="color: #666666">/</span>Jtot;
eta=<span style="color: #666666">0.65*</span>(Eopt<span style="color: #666666">-</span>Ec<span style="color: #666666">-0.3</span>)<span style="color: #666666">*</span>Jsc<span style="color: #666666">*100</span>
<span style="color: #008800; font-style: italic">%% 作效率与Eopt, Ec的二维图</span>
Eopt=[<span style="color: #666666">1</span>:.<span style="color: #666666">01</span>:<span style="color: #666666">3.5</span>]; Ec=[<span style="color: #666666">0</span>:.<span style="color: #666666">01</span>:<span style="color: #666666">1.2</span>];
Jsc=<span style="color: #AA22FF">zeros</span>(<span style="color: #666666">1</span>,<span style="color: #AA22FF">length</span>(Eopt));
<span style="color: #AA22FF; font-weight: bold">for</span> <span style="color: #AA22FF">i</span>=<span style="color: #666666">1</span>:<span style="color: #AA22FF">length</span>(Eopt)<span style="color: #666666">-1</span>
Eintp=[Eopt(<span style="color: #AA22FF">i</span>):dEmin:Emax];
Jintp=interp1(E,J, Eintp, <span style="color: #BB4444">'</span>linear<span style="color: #666666">'</span>);
Jsc(<span style="color: #AA22FF">i</span>)=trapz(Eintp, Jintp<span style="color: #666666">./</span>Eintp)<span style="color: #666666">/</span>Jtot;
<span style="color: #AA22FF; font-weight: bold">end</span>
[x, y]=<span style="color: #AA22FF">meshgrid</span>(Eopt, Ec);
[z, y]=<span style="color: #AA22FF">meshgrid</span>(Jsc, Ec);
eta=<span style="color: #666666">0.65*</span>(x<span style="color: #666666">-</span>y<span style="color: #666666">-0.3</span>)<span style="color: #666666">.*</span>z<span style="color: #666666">*100</span>;
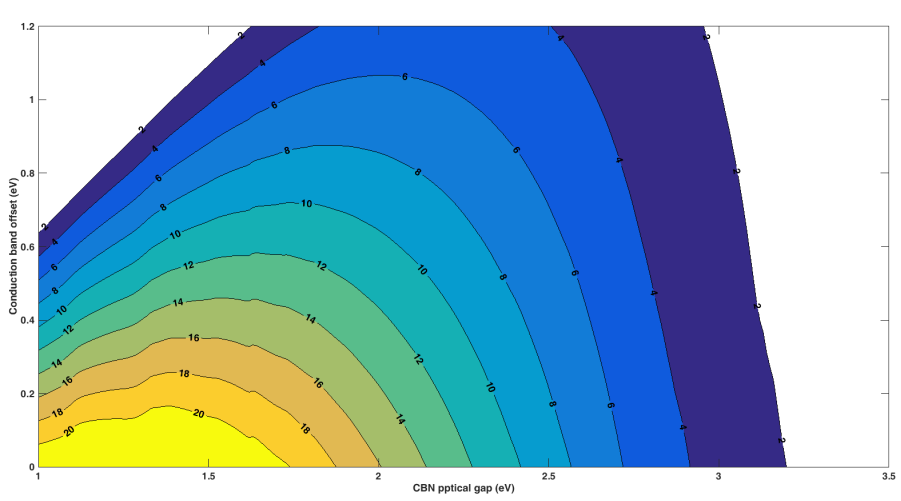
contourf(x,y,eta, [<span style="color: #666666">2</span>:<span style="color: #666666">2</span>:<span style="color: #666666">20</span>], <span style="color: #BB4444">'</span>ShowText<span style="color: #666666">'</span>,<span style="color: #BB4444">'</span>on<span style="color: #666666">'</span>)
xlabel(<span style="color: #BB4444">'</span>CBN pptical gap (eV)<span style="color: #666666">'</span>)
ylabel(<span style="color: #BB4444">'</span>Conduction band offset (eV)<span style="color: #666666">'</span>)
</pre></div>
</td></tr></table>所得图形与论文中 Fig.2 一致.
一些说明
大气层外太阳光谱不受大气的影响,是计算传感器大气层外波段平均太阳辐照度的基础。但由于测量仪器及方法的差别,现有多套太阳光谱曲线数据之间存在一定的差异。本文选用了9条常用的太阳光谱曲线(6S、ASTM-E490、ASTM-G173、Chance、Kurucz、Neckel & Lab、Thuillier、Wehrli 和 WRC 太阳光谱曲线)进行对比分析,以确定最合适计算ESUN b 的太阳光谱。
6S 太阳光谱为 6S 大气辐射传输模型中内置的太阳光谱曲线,光谱范围为 0.25~4.0 μm;ASTM-E490 太阳光谱由美国材料和试验协会(ASTM) 根据卫星、航天飞机、火箭探测、地基太阳望远镜等观测资料发布,光谱范围为 0.12~1000 μm;ASTM-G173太阳光谱由ASTM通过SMARTS模式导出,光谱范围为0.28~4.0 μm;Chance太阳光谱来源于地面和气球观测资料,光谱范围为 0.2~200 μm;Kurucz太阳光谱来源于理论模型和经验模型计算,光谱范围为 0.2~200 μm;Neckel & Lab 太阳光谱由 Neckel 和 Labs 基于对日盘中心绝对强度的观测资料发布,光谱范围为 0.4~2.0 μm;Thuillier 太阳光谱由 Thuillier 等人根据多次航空飞行观测资料发布,光谱范围为 0.2~2.4 μm;Wehrli 太阳光谱由 Wehrli 根据多条太阳光谱整合而成,光谱范围为0.20~3.0 μm;WRC 太阳光谱由 World Radiation Center 机构根据地面和火箭观测数据发布,光谱范围为0.35~2.5 μm。
在地球大气层的上界,距离太阳一个天文单位处,与太阳垂直的单位面积上,单位时间所得的的太阳辐射能量叫一个太阳常数S0。此时把太阳看出点光源,不考虑大气层吸收。但是在实际地球表面附近的太阳辐射强度受大气吸收的影响。大气吸收同时也影响太阳光谱分布。同时辐射强度还受太阳运转的高度影响。为了描述这一关系,引入大气质量(air mass, AM)。太阳穿过大气层垂直射入海平面时的高度作为一个大气质量AM1,辐照度大约1000W/M2,太阳在其他任意位置时穿过大气层的距离与AM1有sina的关系。a为太阳的高度角。外层空间的大气质量为AM0。太阳高度降低时,通过大气层的距离增加。大气质量大于1。最接近现实生活情况下的大气质量为AM1.5。此时太阳高度角为41.8度,辐照度为963W/M2。所以国际标准组织定义AM1.5为地面光伏组件的标准条件,辐照度定为1000W/M2.
ASTM G173–03的AM1.5G光谱采用变步长梯形求积积分,结果为1000.37 W/m2。

