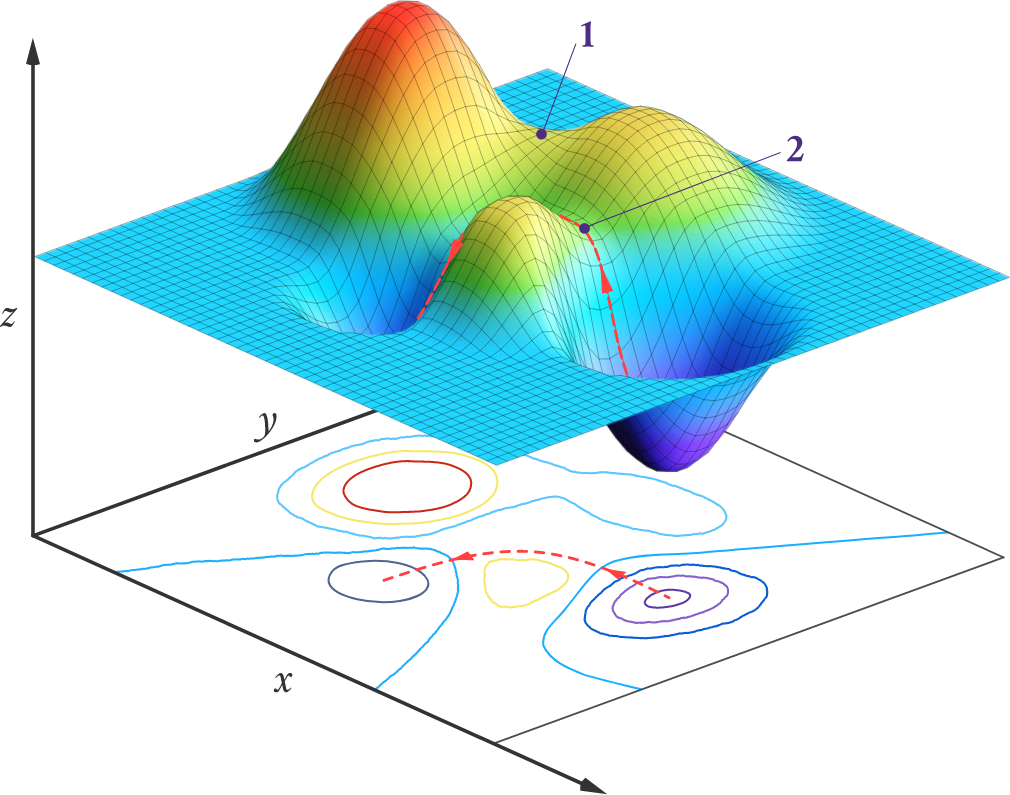
最近有人问起一张势能面模型图, 想用gnuplot或其他绘图工具复刻.

我也尝试着进行了复刻, 最终并没有达到完全相同的效果. 这里记载下相关的信息, 以待来者吧.
根据图形搜索结果, 此图在一些专业论文中有所使用, 查看其引用信息, 则会给出Ümit Kaya via LibreTexts. 据此, 可以追溯到 <a target="_blank" href="https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_\(LibreTexts\)/30%3A_Gas-Phase_Reaction_Dynamics/30.10%3A_The_Potential-Energy_Surface_Can_Be_Calculated_Using_Quantum_Mechanics">Figure 30.10.3: A 2-D contour map and corresponding Potential Energy Surface for a hypothetical endothermic reaction. See the text for a detailed explanation. (CC BY-NC; Ümit Kaya via LibreTexts)</a>. 不出意外的话, 此图来源于此.
此图的原始格式为svg. 但查看其代码则发现, 图像中的彩色表面为嵌入的图像, 各种线条则是绘制的. 我们可以将这两部分分离开来,
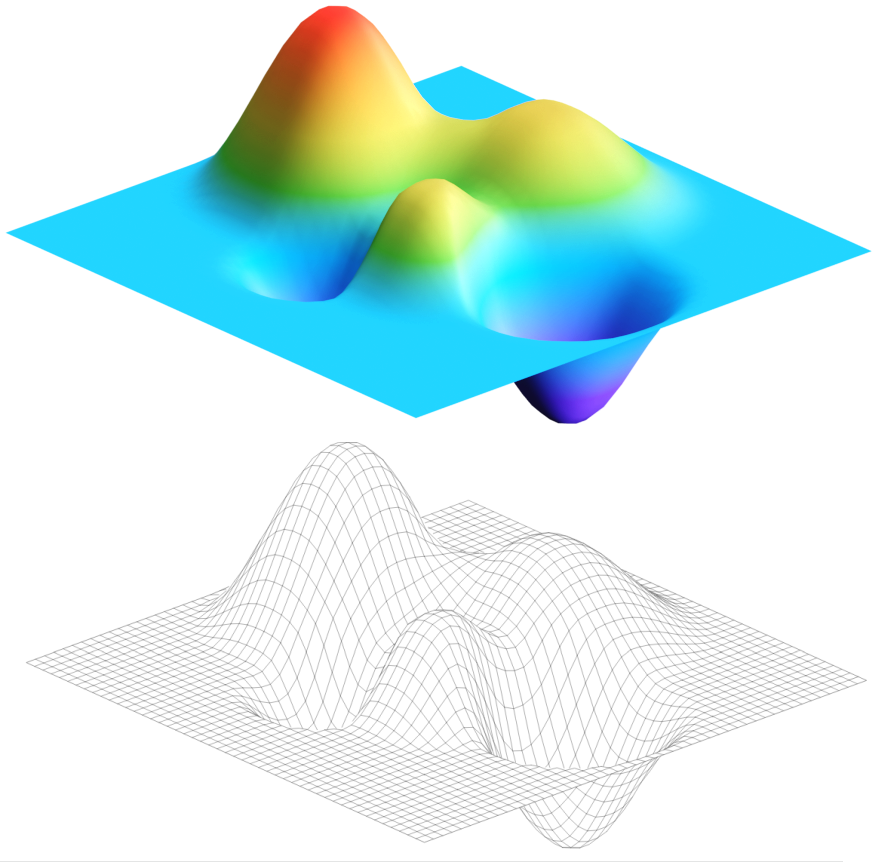
要复刻彩色表面, 有两个要素: 表面的解析表达式与颜色映射方案. 对于前者, 如果接触过matlab绘图, 容易发现这个表面看起来很像matlab的peaks函数
$$╤ z(x, y)&=3(1-x)^2 \exp(-x^2-(y+1)^2) \ &-10({x/5}-x^3-y^5) \exp(-x^2-y^2)\ &-{1/3}\exp(-(x+1)^2-y^2) ╧$$
但是如果绘制出来, 仔细对比, 则发现并不完全一样, 主要区别在于峰的位置和胖瘦. 据此推测原图所用解析表达式并非peaks函数, 而是进行了一定的修改. 我试着改变了表达式中的一些参数设置, 结果都不理想, 觉得瞎试不是办法, 所以要尝试其他方法.
原svg图中给出了表面的网格数据, 据此或许可以反推出表面的表达式. 但所给的网格数据是二维图片上的, 并非三维点. 所以要看能不能根据二维图片上的网格数据反推出对应的三维数据. 理论上讲, 将三维数据绘制到二维平面后, 会丢失一部分信息, 因而是无法完全复原的, 至少被遮挡的部分是没有办法知晓的.
要反推每个二维网格点的三维坐标, 首先需要知道原图使用何种方式将三维点绘制到二维平面上, 也就是计算机图形学中所说的投影. 有多种不同的投影方法, 相关的基础课程, 网络资料也很多.
对大部分比较简单的可视化程序, 采用的投影方式也简单, 一般是正投影, 相机和世界坐标系重合, y轴向上, x轴向左, z轴垂直xy面向外, 投影只是直接地忽略z坐标. 在进行旋转时, 要注意旋转是在哪个坐标系中进行的, 从而确定对应的矩阵应该左乘还是右乘, 详细解释可参考网上的一些讨论
查看原图的展示方式, 当是先x轴转60°, 再z轴转45°, 二者都基于本体坐标系. 据此, 可以推知坐标变换的方法
$$╤ R{x} &=\begin{pmatrix}1 & 0 & 0\cr 0 & \cosθ & -\sinθ\cr 0 & \sinθ & \cosθ\end{pmatrix}\ R{z} &=\begin{pmatrix}\cosφ & -\sinφ & 0\cr \sinφ & \cosφ & 0\cr 0 & 0 & 1\end{pmatrix}\ R=R_xR_z&=\begin{pmatrix}\cosφ & -\sinφ & 0\cr \sinφ\,\cosθ & \cosφ\,\cosθ & -\sinθ\cr \sinφ\,\sinθ & \cosφ\,\sinθ & \cosθ\end{pmatrix}\ ╧ $$
以坐标形式明确写出为:
$$╤ x' &=x \cosφ - y\sinφ \ y' &=(x \sinφ - y\cosφ)\cosθ -z\sinθ \ z' &=(x \sinφ + y\cosφ)\sinθ +z\cosθ \ ╧ $$
重新整理下,
$$╤ x' &=x \cosφ - y\sinφ \ {y'/\cosθ}+z\tanθ &=x\sinφ +y\cosφ ╧ $$
可以得到关系式
$$x'^2+({y'/\cosθ}+z\tanθ )^2=x^2+y^2$$
根据上面的坐标变换公式, 确定图形观察方向$θ, φ$后, 对二维图片上的点$(x', y')$, 只要知晓了其原始坐标$(x, y)$, 即可反推出对应的$z$坐标.
但是, 原svg中所给的网格点毫无规律, 并没有按一定顺序排列(猜测为自动生成的), 所以需要手动或一定算法才能将每个点的坐标对应好. 按当下的流行说法, 要先标注.
假定标注好了网格点, 反推出了对应的$z(x, y)$, 是否可以得到表面的解析式呢? 理论上也是可行的, 只要对所有点进行拟合即可.
至于颜色映射方案, 看原图的效果应当是某种彩虹色, 但与标准的彩虹色有所不同. 再加上绘图表面时进行了光照渲染, 所以吸取的颜色无法直接使用. 若根据$z$坐标进行反推则需要知道表面的表达式以计算法线, 以及所用的光照方法(猜测是最简单Phong), 如果还使用了某种材质的话, 反推出本来的颜色就更困难了.
综上, 对原图进行逆向, 复刻或许可以, 但首先需要对每个点进行标注, 工作繁琐, 只能作为保底的解决方案.
尽管我们无法复刻原图, 但做个类似的完全没问题. 以gnuplot为例, 使用peaks函数, 彩虹jet方案, 效果如下
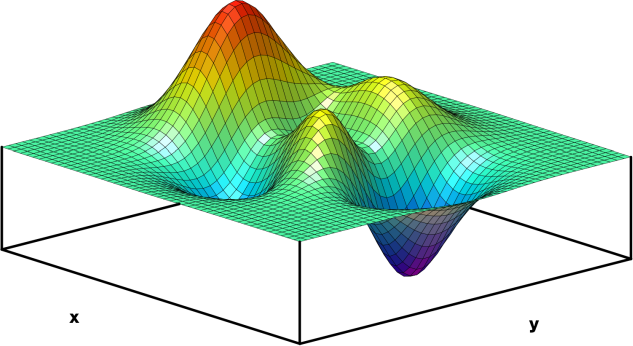
看起来效果还是很接近的.
下面推算peaks函数的驻点, 包括极值点(极大点, 极小点), 鞍点(只有一阶鞍点), 以及驻点间的最小能量途径, 以便绘制示意图.
待补.