在拟合势能函数的时候, 除解析式外, 也可以利用样条函数进行拟合. 样条拟合与其插值正好相反: 已知函数在节点上的值求任意位置的值, 做插值; 已知函数的某些组合值求函数节点上的值, 属于拟合. 由于样条函数可以化为节点函数值的线性表达式, 这样就可以将待求参数线性化, 得到最优情况下函数的形状, 为寻找合适的解析式提供依据, 当然也可以直接利用得到的离散数据拟合解析式.
样条函数可以是零阶, 一阶, 二阶, 三阶或更高阶. 实际使用中, 三阶使用最为普遍. 由于三次样条的构造需要求解一个三对角线性方程组, 其显式解很难得到, 所以线性化结果很繁琐.
在每一区间上样条函数为常量, 函数整体呈台阶状. 对等距情况, 计算时最好使用就近原则, 取最近点的值作为拟合点, 可用i=nint(x/dx)实现.
在每一区间上样条函数为线性函数, 函数整体呈折线状.
$f_i(x)=yi+{y{i+1}-y_i \over \Delta x} (x-x_i)$
此式自动满足函数值连续条件, 即零阶连续.
在每一区间上, 样条函数为二次函数, 整体一阶连续, 即有连续的导数. 但仅有节点的函数值不能唯一确定整个函数, 还须提供某一节点上的导数值, 一般可令端点的导数值为零. 二次样条函数在偶数点的曲率不连续. 由二阶开始, 插值函数不再具有局域性, 改变某一节点, 函数整体都会改变. 使得线性系数分离很困难.
$$\begin{align} f_i(x) &=y_i + k_i (x-xi) + {k{i+1}-k_i \over 2 \Delta x} (x-xi)^2 \ k{i+1} &=-ki+2 {y{i+1}-y_i \over \Delta x}, ki=2 {y{i+1}-yi \over \Delta x}-k{i+1} \end{align}$$
可化简得
$$\begin{align} f_i(x) &= y_i+k_i(x-xi) + (y{i+1}-y_i-k_i \Delta x) ({x-xi \over \Delta x})^2 \ &= \alpha^2 y{i+1} + (1-\alpha^2) y_i + (1-\alpha)\omega k_i \ \alpha &= \omega/\Delta x, \; \omega=x-x_i \end{align}$$
对势能函数, 一般满足远距离处导数为零, 故可使用自然条件 $k_n=0$ , 由此, 可推知所有系数 $k_i$ .
令 $k_i = {2 \over \Delta x} T_i, \Deltai=y{i+1}-y_i$, 则 $T_i$ 满足递推式
$T_i = \Deltai - T{i+1}$
可求得
$$\begin{align} Ti = \sum{j=i}^{n-1} (-1)^{j-i} \Delta_j \end{align}$$
样条函数可写为
$fi(x)=\alpha^2 y{i+1} + (1-\alpha^2) y_i + 2\alpha(1-\alpha)T_i, \; \alpha = (x-x_i)/\Delta x$
对不等距划分, 令 $$\Deltai={y{i+1}-yi \over x{i+1}-x_i}$$, $k_i$ 满足如下递推式
$k_i = 2 \Deltai -k{i+1}$
求得
$$\begin{align} ki = 2 \sum{j=i}^{n-1} (-1)^{j-i} \Delta_j \end{align}$$
对等距划分的均匀样条, 设节点为 $1, 2,....n$, 若 $$x \in [xi, x{i+1}], a=x-xi, b=x{i+1}-x, a+b=h=\Delta x$$, 则
$$6 h fi(x) = 6(a y{i+1}+b yi) + a(a^2-h^2)M{i+1} + b(b^2-h^2)M_i$$
$M_i$ 为节点的二阶导数, 对应于力学上的弯矩, 满足下面的方程
$$Mi + 4 M{i+1} + M{i+2} = d{i+1} = {6 \over h^2} (y{i+2}-2y{i+1}+y_i), \ i=1,2...n-2$$
要求的 $M_i$ 个数为 $n$, 而对应的方程数目为 $n-2$, 故还需两个边界条件才能唯一确定, 边界条件可取为两端点的导数值或是二阶导数值. 常用的自然边界条件指 $$M_1=M_n=0$$. 加上边界条件后便可求得 $$M_2, M3, ...M{n-1}$$
$M_i$ 满足的方程为
$$\begin{matrix} 0 &+ & 4M_2 &+ & M_3 &= &d_2 \ M_2 &+ & 4M_3 &+ & M_4 &= &d_3 \ M_3 &+ & 4M_4 &+ & M_5 &= &d4 \ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ M{n-3} &+ & 4 M{n-2} &+ & M{n-1} &= &d{n-2} \ M{n-2} &+ & 4 M{n-1} &+ & 0 &= &d{n-1} \end{matrix}$$
写为矩阵形式
$$\begin{bmatrix} 4 & 1 & 0 & \cdots \ 1 & 4 & 1 & \cdots \ \vdots & \vdots & \vdots & \vdots \ \cdots & 1 & 4 & 1 \ \cdots & 0 & 1 & 4 \ \end{bmatrix} \left[ \begin{array}{c} M_2 \ M3 \ \vdots \ M{n-2} \ M_{n-1} \end{array} \right] =\left[ \begin{array}{c} d_2 \ d3 \ \vdots \ d{n-2} \ d_{n-1} \end{array} \right]$$
可见, 此方程为三对角方程组, 对角占优, 存在唯一解, 可利用所谓的追赶法求解. 中文常称的追赶法, 是Thomas方法的形象翻译. 大致求解过程分为两步:
追: 利用消元法将原方程化为二对角方程, 向前递推, 使系数矩阵主对角线变为1. 由第一个方程, 得到 $M_2$ 和 $M3$ 的关系, 将其带入第二个方程, 消去主对角线下方系数. 以此进行, 最终追到 $M{n-1}$, 得到其解. 变换后, 其方程为
$$\begin{bmatrix} 1 & A_2 & 0 & \cdots \ 0 & 1 & A3 & \cdots \ \vdots & \vdots & \vdots & \vdots \ \cdots & 0 & 1 & A{n-2} \ \cdots & 0 & 0 & 1 \ \end{bmatrix} \left[ \begin{array}{c} M_2 \ M3 \ \vdots \ M{n-2} \ M_{n-1} \end{array} \right] =\left[ \begin{array}{c} D_2 \ D3 \ \vdots \ D{n-2} \ D_{n-1} \end{array} \right]$$
赶: $M_{n-1}$ 已经追得, 然后由此倒推, 得到其他 $M_i$ 值.
对上面的方程, 由于系数是固定的, Thomas方法的递推式为
$$\begin{align} A_2 &= {1 \over 4}, & Ai &= {1 \over 4-A{i-1}} \ D_2 &= A_2 d_2, & D_i &= A_i(di-D{i-1}) \ M{n-1} &= D{n-1}, & M_i &= D_i-Ai M{i+1} \end{align}$$
对 $A_i$, 可求得其通式
$A_i=2-\sqrt{3} \dfrac{t^i+1} {t^i-1}, t=(2+\sqrt{3})^2$
对 $D_i$, 向后递推至 $D_2$, 一般项可写为
$$\begin{align} Dj = \sum{k=2}^j (-1)^{j-k} P_k^j d_k \end{align}$$
对 $Mi$, 向前递推至 $M{n-1}$, 一般项可写为
$$\begin{align} Mi = \sum{j=i}^{n-1} (-1)^{j-i} P_i^{j-1} D_j \end{align}$$
综合上面两个结果, 得到
$$\begin{align} Mi &= \sum{j=i}^{n-1} \sum_{k=2}^j (-1)^{2j-i-k} P_i^{j-1} P_k^j dk \ &= \sum{j=i}^{n-1} \sum_{k=2}^j (-1)^{i+k} P_i^{j-1} P_k^j d_k, \; i=2,3,...n-1 \ Pm^n &= \prod{l=m}^n A_l = Am A{m+1} \ldots A_{n-1} A_n, \; n>m \ \end{align}$$
根据插值公式
$$\begin{align} dk &= {6 \over h^2} (y{k+1}-2yk+y{k-1}) \ 6 h fi(x) &= 6(\alpha y{i+1}+\beta yi) + \alpha(\alpha^2-h^2)M{i+1} + \beta(\beta^2-h^2)M_i \end{align}$$
以划分间距 $h$ 为单位, 约化上述公式
$$\begin{align} fi(x) &= \alpha y{i+1}+\beta yi + \alpha(\alpha^2-1)\mu{i+1} + \beta(\beta^2-1) \mu_i \ \alpha &={a \over h}, \beta={b \over h}=1-\alpha, \mu_i={M_i \over 6/h^2} \end{align}$$
由此可见, 虽然三次样条函数仍可写为节点值的线性形式, 但其系数十分复杂.
上面公式看起来清楚, 但是实际计算时需要计算 $Mi$ 和 $M{i+1}$, 两个三重循环, 整体计算量为 $O(N^3)$. 利用 $A_i$ 的近似关系和 $M_i$ 的递推关系可以将公式的计算量减少一些.
$$\begin{align} fi(x) &= \alpha y{i+1}+\beta yi + \alpha(\alpha^2-1)\mu{i+1} + \beta(\beta^2-1) \mui \ &= \alpha y{i+1}+\beta y_i + \beta(\beta^2-1) D_i \ &+ [\alpha(\alpha^2-1)-\beta(\beta^2-1)Ai] \mu{i+1} \end {align}$$
对不等距划分, 上面的递推公式太过复杂, 很难写出一般项了. 样条函数可写为
$$\begin{align} fi(x) &= {a y{i+1} + by_i \over hi} + {a(a^2-h^2)M{i+1}+b(b^2-h^2)M_i \over 6h_i} \ hi &= x{i+1}-x_i, a=x-x_i, b=h_i-a \end{align}$$
$M_i$ 满足方程
$$\begin{align} h_i M_i + 2(hi+h{i+1}) M{i+1} + h{i+1}M{i+2} \ = 6( {y{i+2}-y{i+1} \over h{i+1}} - {y_{i+1}-y_i \over h_i} ), \ i=1,2,\cdots,n-2 \end{align}$$
awk实现的代码如下
利用Matlab的csape函数可以进行三次样条函数的插值, 示例代码如下
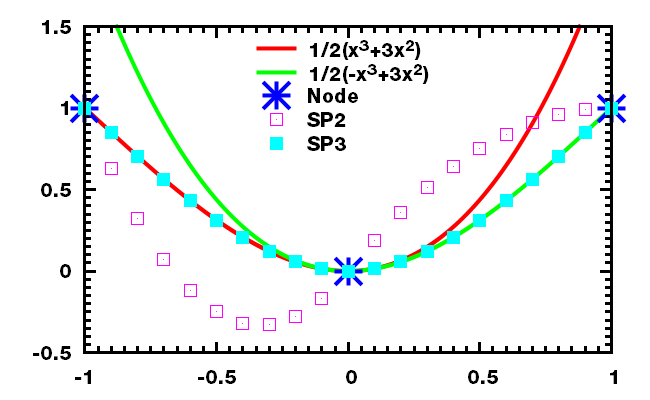
几个测试函数的结果

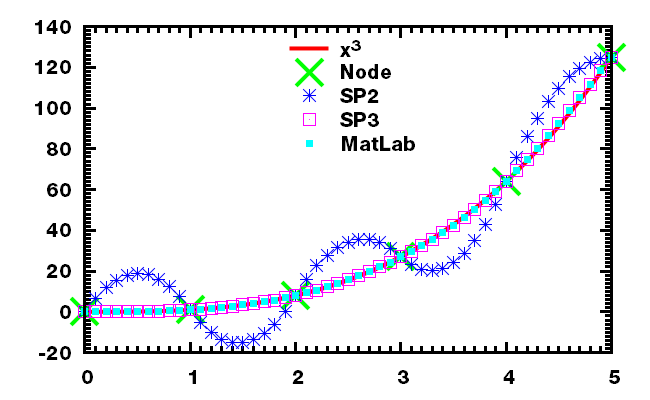
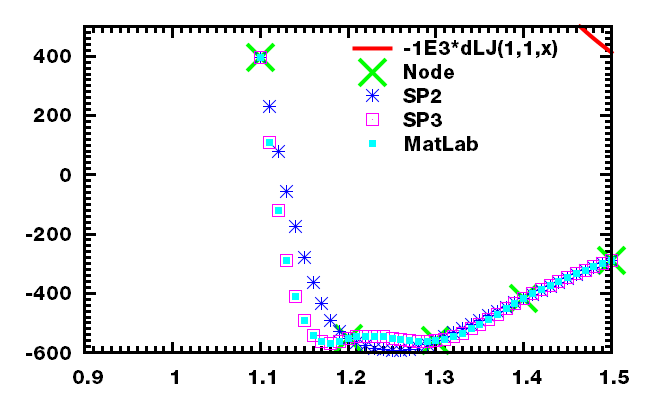
对已经拟合的样条函数进行数值积分时可利用可利用Simpson方法. Simpson方法具有三阶精度, 对不超过三次的多项式精确成立, 很适合于二次和三次样条函数.