球谐函数是一类特殊函数. 虽说被称为特殊函数, 其实它们并没有什么特殊的地方, 只不过比那些常见的指数函数、三角函数稍微复杂一些而已, 你一旦熟悉了它们的性质, 就不会再觉得它们有什么特殊了.
这类特殊函数之所以在物理、化学和计算机科学中都有着重要应用, 是因为它们的独特性质:
由性质1, 我们可以把原子波函数的角度部分展开为球谐函数的线性组合. 化学物理中为人熟知的原子轨道的角度部分就是球谐函数, 常用的spdf轨道实际就是经过处理的几个球谐函数.
对性质2, 在计算机图形学的形状识别中有着重要应用, 许多识别算法就是基于球谐函数的旋转不变性.
定义:基于缔合Legendre多项式(Associated Legendre Polynomial)
$\mathrm Y_l^m = \sqrt{ {2l+1\over4\pi} {(l-m)!\over(l+m)!} } \mathrm P_l^m(\cos\theta) \mathrm e^{im\phi}, m \in Z, \theta \in [0,\pi], \phi \in [0,2\pi]$
此定义式对m正负无要求, 故
$\mathrm Y^{\bar m}_l = \sqrt{ {2l+1\over4\pi} {(l+m)!\over(l-m)!} }\mathrm P_l^{\bar m}(\cos\theta) \mathrm e^{-im\phi}$
缔合Legendre多项式
$\mathrm P_l^m(x) = (-1)^m (1-x^2)^{m/2} {\mathrm d^m \over \mathrm dx^m} \mathrm P_l(x), m>0$
若m取负值时, 定义为
$\mathrm P_l^{\bar m} = (-1)^m {(l-m)! \over (l+m)!} \mathrm P_l^m(x)$
故
$\mathrm Y^{\bar m}_l = \sqrt{ {2l+1 \over 4\pi} {(l+m)! \over (l-m)!} } (-1)^m {(l-m)! \over (l+m)!} \mathrm P_l^m(\cos\theta)\mathrm e^{-im\phi} = \sqrt{ {2l+1 \over 4\pi} {(l-m)! \over (l+m)!} } (-1)^m \mathrm P_l^m(\cos\theta)\mathrm e^{-im\phi} =(-1)^m (\mathrm Y_l^m)^*$
$(-1)^m$ 项称为Condon-Shortley相因子, 有人会省略此项, Mathematica计算时会考虑此项.
此外, $\mathrm Y_l^m(-\theta, -\phi) = [\mathrm Y_l^m(\theta,\phi)]^*$
由于Legendre多项式归一化条件为
$$\int_{-1}^1 \mathrm Pl^m(x) \mathrm P{l'}^m(x) dx = {2 \over 2l+1} {(l+m)! \over (l-m)!} \delta_{ll'}$$
$$\int_{-1}^1 \mathrm Pl^m(x) \mathrm P{l'}^{\bar m}(x) dx = (-1)^m {2 \over 2l+1} \delta_{ll'}$$
故可定义归一化Legendre多项式为
$\hat {\mathrm P}_l^m(x) = \sqrt{ {2l+1 \over 2} {(l-m)! \over (l+m)!} } \mathrm P_l^m(x), m \in Z$
$\hat {\mathrm P}_l^{\bar m}(x) = (-1)^m \hat{\mathrm P}_l^m(x)$
其最大值为 $\mathrm P_l^0(\pm 1)=\sqrt{2l+1 \over 2}$ 满足归一化条件
$\int_{-1}^1 \hat {\mathrm P}_l^m(x) \hat {\mathrm P}_l^m(x) dx = 1$
$\int_{-1}^1 \hat {\mathrm P}_l^m(x) \hat {\mathrm P}_l^{\bar m}(x) dx = (-1)^m$
利用归一化条件, 我们可以重新定义球谐函数为
$\mathrm Y_l^m = {1 \over \sqrt{2\pi}} \hat {\mathrm P}_l^m(\cos\theta) \mathrm e^{im\phi}$
$|\mathrm Y_l^m| = {1 \over \sqrt{2\pi}} \hat{\mathrm P}_l^m(\cos\theta)$
$\Re{\mathrm Y_l^m} = {1 \over \sqrt{2\pi}} \hat{\mathrm P}_l^m(\cos\theta) \cos m\phi$
$\Im{\mathrm Y_l^m} = {1 \over \sqrt{2\pi}} \hat{\mathrm P}_l^m(\cos\theta) \sin m\phi$
其中, $\hat{\mathrm P}_l^m$ 为归一化的Legendre多项式.
因此, 球谐函数归一化条件可写为
$$\int0^{2\pi}d\phi \int{-1}^{1} (\mathrm Y_l^m)^* \mathrm Y_l^m dx = \int0^{2\pi}d\phi \int{-1}^{1} {1 \over 2\pi} \hat{\mathrm P}_l^m(x) \hat {\mathrm P}_l^m(x) dx = 1$$
${\mathrm Y}_l^m$ 的计算实际上归结为计算缔合Legendre多项式 ${\mathrm P}_l^m$, 根据不同需要, 可适当采取下面几种方法:
计算 ${\mathrm Y}_l^m$ 时须计算 $\sin(m \phi), \cos(m\phi)$, 由于三角函数的计算较多项式为慢, 因此可利用三角公式将其展开为 $\sin\phi, cos\phi, \sin^2\phi, \cos^2\phi$ 的多项式. 下面是m到6时的公式:
$\sin2\phi=2\sin\phi \cos\phi, \cos2\phi=\cos^2\phi-\sin^2\phi$
$\sin3\phi=\sin\phi(-\sin^2\phi+3\cos^2\phi), \cos3\phi = \cos\phi(\cos^2\phi-3\sin^2\phi)$
$\sin4\phi=4\sin\phi \cos\phi(\cos^2\phi-\sin^2\phi), \cos4\phi = 1-8\sin^2\phi \cos^2\phi$
$\sin5\phi=\sin\phi[1+4\cos^2\phi(\cos^2\phi-3\sin^2\phi)], \cos5\phi = \cos\phi[1+4\sin^2\phi(\sin^2\phi-3\cos^2\phi)]$
$\sin6\phi=\sin\phi \cos\phi[6-32\sin^2\phi \cos^2\phi], \cos6\phi=(\cos^2\phi-\sin^2\phi)(1-16\sin^2\phi \cos^2\phi)$
当然, 这些优化方法只有你需要大量计算 ${\mathrm Y}_l^m$ 时才能提高点速度, 对于普通情况, 你很可能感觉不到计算速度的变化.
下面是一些相关函数的图像.

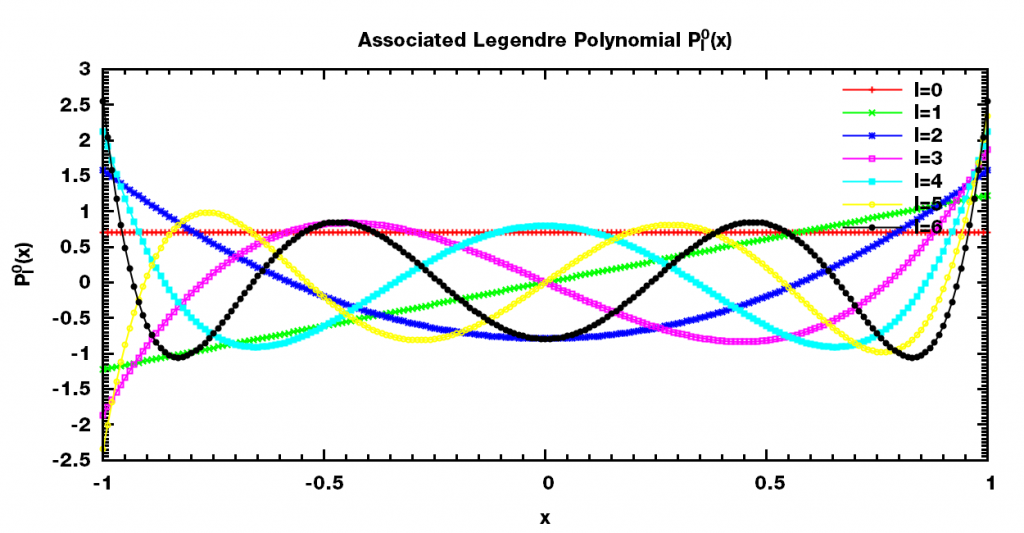
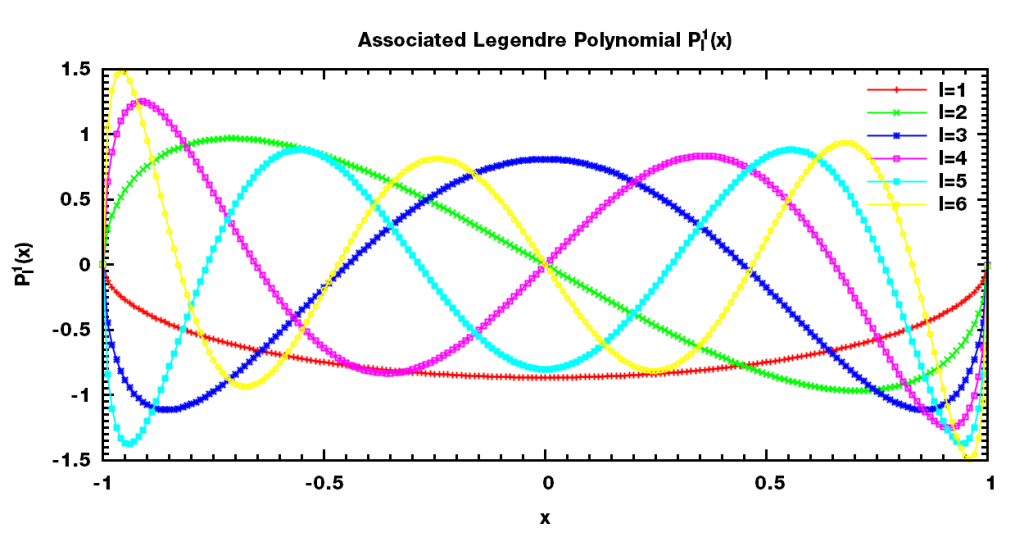
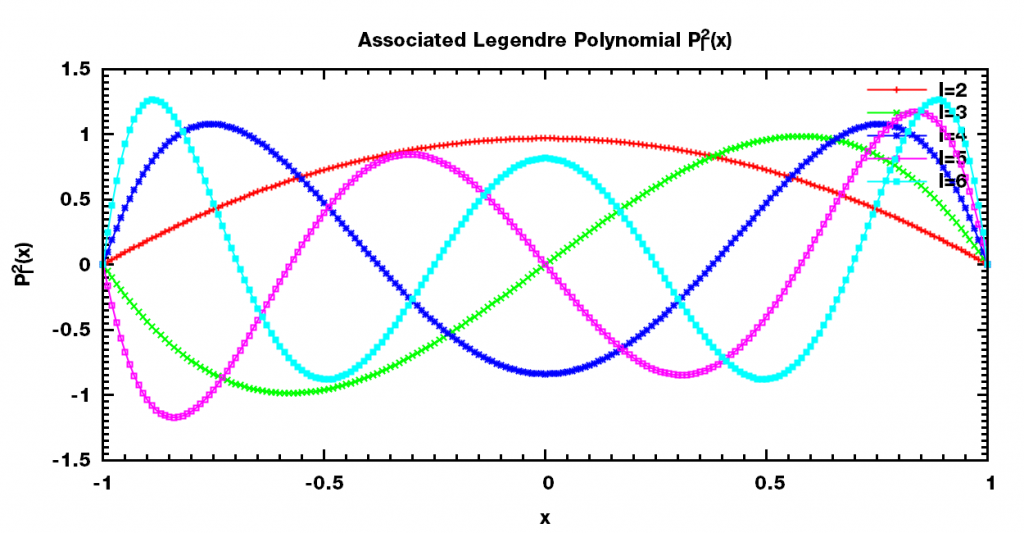
可以看出, $\mathrm P_l^0(x)$ 也就是通常所说的Legendre多项式, 为l阶多项式; $\mathrm P_l^m(x)$ 的奇偶性与l+m的奇偶一致.
参考