仓库源文，站点原文

layout: post title: 电导弛豫法测材料的氧表面交换系数和体相扩散系数 categories:

• 科 tags:
• 编程
• matlab math: true

2013-08-22 18:23:33 感谢网友yiqieke整理此文

背景

钙钛矿混合导体氧化物同时具有氧离子导电性和电子导电性, 因此已被广泛地用作固体氧化物燃料电池的阴极和透氧膜. 这类材料的性能主要由氧在其表面的交换速率以及氧在其体内的扩散速率决定. 如果可以提高这两个速率, 固体氧化物燃料电池和透氧膜的操作温度将会降低, 而在较低温度下工作的燃料电池其材料的老化程度将会有所降低, 并且寿命会更长. 因此, 如何提高这两个速率就成为了很多燃料电池和透氧膜材料研究者所感兴趣的问题. 为此, 对不同的材料我们需要测量其氧表面交换系数和体相扩散系数.

目前测定氧表面交换系数和体相扩散系数的方法主要有同位素交换法和电导弛豫法（ECR, Electrical Conductivity Relaxation）. 由于电导弛豫法所需仪器相对简单, 故应用广泛.

原理

由于钙钛矿混合导体氧化物中存在多价态的过渡金属离子（Fe、Co等）, 在一定温度下突然改变氧化物所处环境的氧分压会造成过渡金属离子的变价, 同时氧化物中的氧（离子）浓度也发生变化. 若在初始时刻（ $t=0$ ）时氧的平衡浓度是 $C_0$ , 当外界氧分压发生突变后, 氧在t时刻的浓度为 $C_t$ . $C_0$ 到 $C_t$ 的变化是通过氧扩散进出氧化物来实现的, 这种扩散会引起体系电导率 $\sigma$ 的变化. 假定体系电导率和氧浓度之间存在线性关系, 则

$${C0-C\infty \over Ct-C\infty} = {\sigma0-\sigma\infty \over \sigmat-\sigma\infty}$$

其中, $\sigma_0$ 为初值时刻（ $t=0$ ）电导率, $\sigmat$ 为氧分压突变后t时刻的电导率, $\sigma\infty$ 为氧浓度重新达到平衡稳定后电导率.

为求得氧的表面交换系数和体相扩散系数, 需要对扩散过程进行求解.

对扩散过程, Fick第一定律指出扩散通量与浓度梯度成正比, 其比例系数为扩散系数：

$\mathbf J=-D \nabla C$

由质量守恒定律,

${\partial C \over \partial t} +\nabla \cdot \mathbf J=0$

进而得到Fick第二定律

${\partial C \over \partial t} -\nabla \cdot D\nabla C=0$

若扩散系数D为常数, 与浓度无关, 则

${\partial C \over \partial t} = D\nabla^2 C$

对于最简单的一维情况

${\partial C \over \partial t} = D{\partial^2 C \over \partial^2 x}$

当 $x \in [-a, a]$ 时, 其边界条件为

$$\begin{split} J(a)&=-D{\partial C \over \partial x}|{x=a}=K[C(a)-C(\infty)] \ J(-a)&=-D{\partial C \over \partial x}|{x=-a}=-K[C(-a)-C(\infty)] \end{split}$$

其中K为交换系数. 设初始浓度 $C(x,0)=C_0$, 利用本征函数展开, 可将方程的解可写为

$${C(x,t)-C_0 \over C(\infty)-C0} = 1-\sum\limits{i=1}^{\infty} {2L_\alpha \cos(\alpha_i x/a) \over (\alphai^2+L\alpha^2+L_\alpha)\cos\alpha_i}\exp(-{t \over \tau_i})$$

时间常数 $\tau_i={a^2 \over D\alpha_i^2}$, 变量 $\alpha$ 满足方程 $\alpha_i \tan(\alphai)=L\alpha={aK \over D}$

实际测量时得到的是浓度的平均值, 所以需要求出整个区间上浓度的平均值,

$$\begin{split} {\bar C(x,t)-C_0 \over C(\infty)-C0} &= 1-{1 \over 2a}\int\limits{-a}^{a}\sum\limits{i=1}^{\infty} {2L\alpha \cos(\alpha_i x/a) \over (\alphai^2+L\alpha^2+L_\alpha)\cos\alpha_i}\exp(-{t \over \taui})dx \ &=1-{1 \over 2a}\sum\limits{i=1}^{\infty} {2L_\alpha \over (\alphai^2+L\alpha^2+L_\alpha)\cos\alpha_i}\exp(-{t \over \taui})\int\limits{-a}^{a} \cos(\alphai x/a) dx \ &=1-\sum\limits{i=1}^{\infty} {2L_\alpha^2 \over \alpha_i^2 (\alphai^2+L\alpha^2+L_\alpha)}\exp(-{t \over \tau_i}) \end{split}$$

上式有两种极限情形：

1. $$K \ll D/a, L_\alpha \to 0$$, 此时 $\tau_i$ 增长很快, 只取第一项, $\alpha_1 \tan\alpha_1 \simeq \alpha1^2=L\alpha$, 故

   $$\begin{split} {\bar C(x,t)-C_0 \over C(\infty)-C0} &= 1-{2L\alpha^2 \over \alpha_1^2(\alpha1^2+L\alpha^2+L_\alpha)}\exp(-{t \over \tau_1}) \ &=1-\exp(-{Kt \over a}) \end{split}$$

2. $K \gg D/a, L_\alpha \to \infty$, 此时 $\alpha_i=(i+{1 \over 2})\pi$,

   ${\bar C(x,t)-C_0 \over C(\infty)-C0} = 1- {8 \over \pi^2} \sum\limits{i=0}^{\infty} {1 \over (2i+1)^2} \exp(-{(2i+1)^2\pi^2 Dt \over 4a^2})$

按这两种极限情况进行数据处理都无法得到氧交换系数K, 还需借助其他的关系式.

上面的方程可以推广到三维, 设三维区间长宽高分别为2a, 2b, 2c, 则

$${\bar C(x,t)-C_0 \over C(\infty)-C0} = 1-\sum\limits{i=1}^{\infty} \sum\limits{j=1}^{\infty} \sum\limits{k=1}^{\infty} A{ijk} \exp(-{t \over \tau{ijk}})$$

$$\begin{align} A{ijk} &={8 L\alpha^2 L\beta^2 L\gamma^2 \over \alpha_i^2 \beta_j^2 \gamma_k^2 (\alphai^2+L\alpha^2+L_\alpha) (\betaj^2+L\beta^2+L_\beta) (\gammai^2+L\gamma^2+L\gamma) } \ {1 \over \tau{ijk}} &= {1 \over \tau_i }+{1 \over \tau_j }+{1 \over \tau_k } \end{align}$$

$$\tau_i = {a^2 \over D \alpha_i^2}, \tau_j = {b^2 \over D \beta_j^2}, \tau_k = {c^2 \over D \gamma_k^2}$$

$$\alpha_i \tan(\alphai)=L\alpha={aK \over D}, \beta_j \tan(\betaj)=L\beta={bK \over D}, \gamma_k \tan(\gammak)=L\gamma={cK \over D}$$

实验

测量条状测试样品的尺寸.

用四探针电导法测定长方体样品的电导率 $\sigma_0$, 然后瞬间改变样品所在气氛的氧分压（比如从0.21 atm变到0.01 atm）, 并记录固定时间间隔（如10s）处的电导率值 $\sigmat$. 当重新达到平衡后, 记录其电导率值 $\sigma\infty$.

实验结果与数据处理

利用所测 $$\sigma0, \sigma\infty, (t, \sigma_t)$$ 计算 $$S(t) = {\sigma0-\sigma\infty \over \sigmat-\sigma\infty}$$, 对 $S(t)$ 进行最小二乘拟合, 便可求出氧表面交换系数K和体相扩散系数D.

这是一个典型的非线性拟合问题, 利用MatLab编写代码时须注意 $\alpha, \beta, \gamma$ 需要在每一步拟合时进行求解, 这可借助于fsolve函数实现.

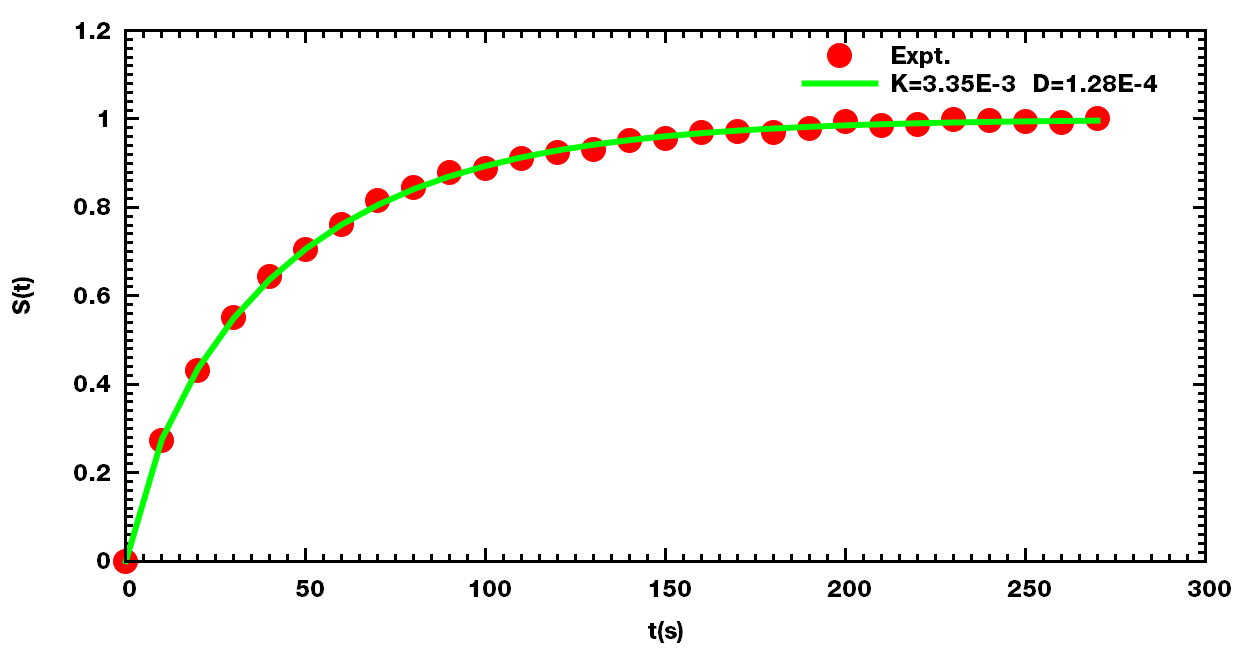
下面是某次实验所得数据及拟合结果.

参考

1. 王严东, 吕喆, 魏波. 无机材料学报, 25(6):635-640, 2010
2. C.-R. Song, H.-I. Yoo. Solid State Ionics, 124:289-299, 1999
3. R.A. Cox-Galhotra, S. McIntosh. Solid State Ionics, 181:1429-1436, 2010
4. M.W. den Otter, A study of OXYGEN TRANSPORT in mixed conducting oxides using isotopic exchange and conductivity relaxation

代码