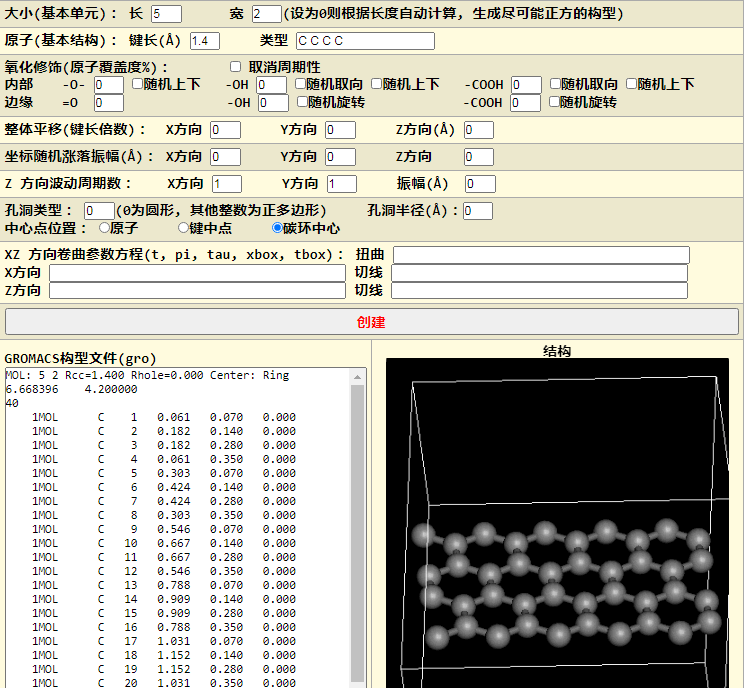
平面石墨烯结构很容易构建, 如何将石墨烯卷曲成需要的形状?
在研究中, 我们肯定会遇到问题. 这毫无疑问. 我们之所以要做研究, 就是因为存在问题. 我们的研究要顺利进行下去, 就要把遇到的问题一一解决. 这些问题有大有小, 有难有易, 无论大小难易, 也无论最终能否成功解决, 都需要我们积极思考, 尝试着分析问题, 看这些问题能否与已知问题联系起来, 然后查阅资料寻找解决方案. 很多时候, 我们的问题也出现在其他领域中, 并已经有了解决方案, 我们只要借助他们的方法就能顺利解决. 这样我们在解决问题的同时, 也扩大了自己的知识库, 锻炼了自己解决问题的能力. 积累的经验越多, 知识库越大, 知识之间的联系越紧密, 解决新问题的能力也就越强. 这些才是做研究的本质所在. 面对问题, 如果你只是要找一个答案, 而舍弃了自己的思考, 没有习惯这种模式, 那么再遇到新问题时, 仍然会感到无从下手.
在尝试解决问题之前, 最好先从理论上分析一下问题, 试着将问题化归为数学问题. 一般而言, 一个问题如果能化归为数学问题, 至少已经解决了一半. 如果数学上已经有了解决方法, 那这个问题就算解决了. 数学上不可解的问题也有很多, 这时在实际中也有各自的应对之道.
我们面对的这个具体问题, 在数学上是两个曲面的映射问题, 大致属于微分几何的研究范围. 一般来说, 对于任意的两个曲面, 是没有通用方法做到精确映射的. 如果两个曲面可以映射, 需要满足一定的条件. 我不是数学家, 没有能力给出这些条件的精确定义. 简单的例子就是你没法把一个环面映射到一个球面. 再一个例子是地图. 我们没有办法精确地绘制地图, 因为没有办法将球面映射到平面而不产生变形, 所以必须采用一定的约束条件, 比如保持距离不变, 或保持角度不变等才能绘制出相应的地图.
但我们的问题有点特殊, 要将平面结构的石墨烯映射到一个曲面上. 正如前一段所讲, 如果目标曲面是球面, 是没法做到精确映射的, 正如不存在表面只有六边形的足球. 这样的问题在计算机游戏模型的贴图中会遇到, 一般称为UV展开, 所以不算个新问题, 能够解决. 但这种解决方法操作起来并不简单, 所以我们继续分析一下, 看能不能进一步简化.
下一步简化就是忽略石墨烯的宽度, 将其视为沿长度方向的一条直线, 卷曲时也局限在一个平面内, 这相当于将一根柔性直线弯曲成目标曲线. 在这种条件下, 我们可以根据距离不变的条件将这条直线上的点精确地映射到目标曲线上. 这里的距离不变意味着, 直线的长度和距离会转变为目标曲线的弧长. 所以, 我们的问题就转化为如何将直线长度和曲线弧长联系起来. 为此, 我们需要对目标曲线进行弧长参数化.
一旦知道了 弧长参数化 这个关键词, 你就可以搜到大量资料. 这也说明, 对具体的问题, 只有化归为适当的数学问题, 才能找到恰当的关键词, 并进而找到解决方法. 如果我们直接搜索 石墨烯卷曲变形 之类, 大概是很难找到合适解决方法的. 确定搜索关键词在解决问题时是非常关键的一步. 知识库越大, 知识间的联系越多, 就越容易触类旁通, 确定恰当的关键词.
任意曲线的弧长参数化很难求得解析式, 大多只能使用数值方法来求解. on the arc length parametrization problem对此有比较宽泛的讨论, 并说明了困难所在. 举例来说, 即便对于简单的二次曲线, 弧长参数化后所得的表达式也很复杂.
在这里, 发散思维一下. 是不是存在简单的弧长参数曲线, 且容易调节, 像贝塞尔曲线一样? 如果存在的话, 我们可以用它来近似任意曲线, 等分长度也很方便, 应该有很多应用. 略微查了一下, 没有发现相关的文献. 或者, 这个想法并不好, 或者这种方法没有解. 无论如何, 这是个值得思考的问题. 在查阅已有解决方案时, 我们也不能放弃自己的思考, 先理解这些方案, 再尝试看自己能不能有新的想法. 大多数想法可能都是没有结果的, 但这个过程值得. 这也是锻炼的一部分.
到现在我们已经确定没法用解析方法做了, 那就使用数值方法吧. 数值方法虽然不优雅, 数学上显得比较脏, 但胜在简单粗暴, 在科学工程中的应用也更广泛. 任给曲线的参数 $t$ 方程, 要计算任意 $t$ 时对应的弧长 $s$, 使用数值积分即可. 反过来, 任给弧长 $s$, 反求参数 $t$, 可以用二分法, 从大的范围开始, 不断缩小范围, 只到具有一定的精确度.
这方面的资料就很多了. 在游戏中, 要想让目标沿某个曲线匀速运动, 就需要进行弧长参数化处理.
好了, 我们现在已经找到解决方法了, 将它写成代码实现一下, 然后测试, 看结果是否正确.
先看看默认的石墨烯.

在我们的石墨烯模型中, 长沿x方向, 宽沿y方向, 所以我们可以在x-z平面内弯曲它. 这样我就需要给出x-z平面内目标曲线的参数方程. 最简单的参数曲线, 就是倾斜的直线
$$x=t \ z=t$$
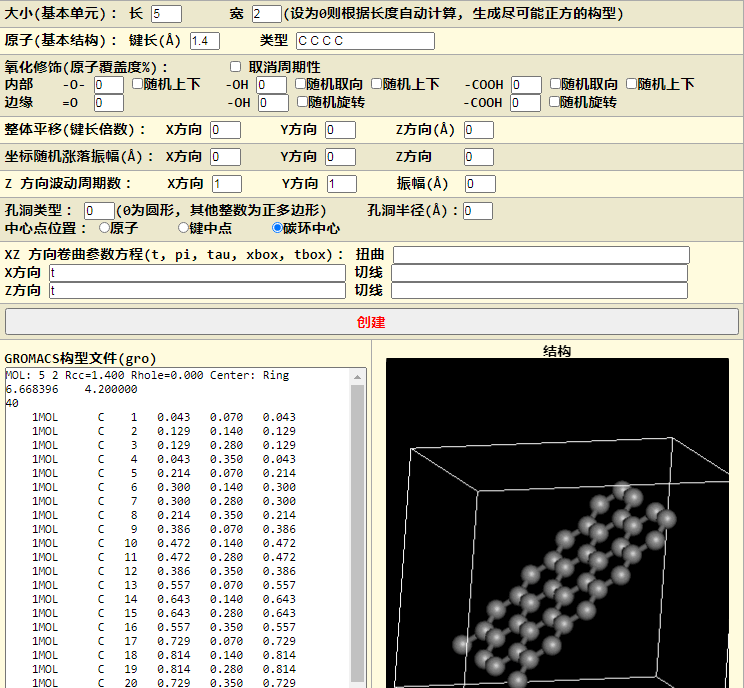
石墨烯沿 $z=x$ 方向倾斜起来, 符合预期.
上面这个例子很平凡, 结果也容易预期, 但程序的处理流程是一样的, 所以很适合用以测试代码的正确性. 如果这样简单的情况下代码都无法给出正确的结果, 那代码肯定有问题. 如果上来就用复杂的情形来测试代码, 你可能需要花费更多的时间才能确定问题所在.
简单的测试通过了, 下面就测试个更复杂点的, 圆弧
$$x=\cos(t) \ z=\sin(t)$$
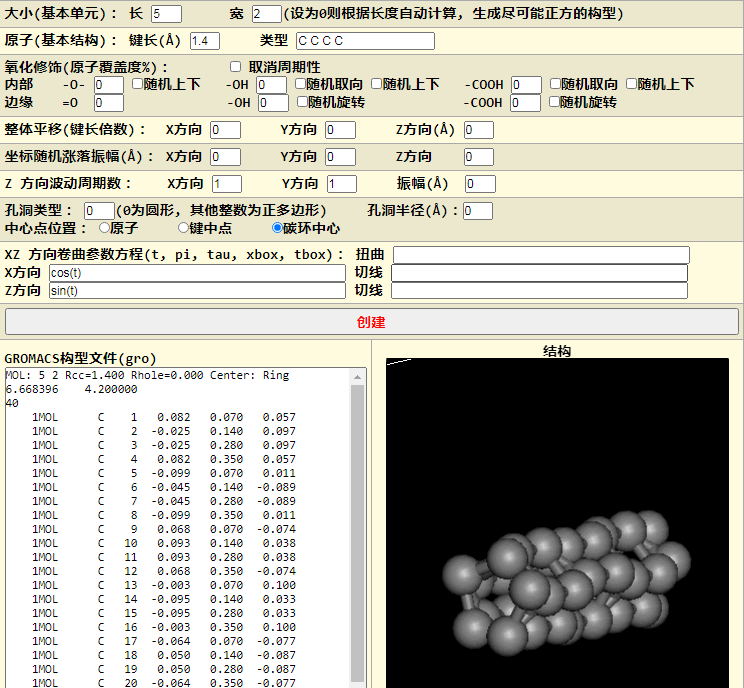
可以看到, 卷曲起来了, 但是由于半径太小, 所以原子发生了重叠. 为方便指定半径和卷曲角度, 我们可以使用程序中已经定义的常量, pi, tau(2 pi), xbox(x方向盒子长度).
卷曲成半圆
$$x=\text{xbox/pi}\cos(t) \ z=\text{xbox/pi}\sin(t)$$
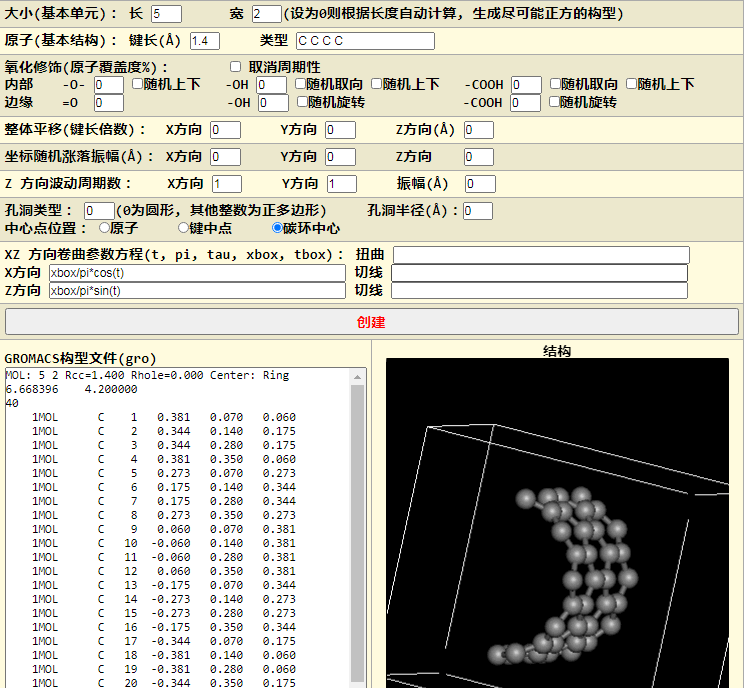
卷曲成整个圆, 也就是规则的碳管
$$x=\text{xbox/tau}\cos(t) \ z=\text{xbox/tau}\sin(t)$$
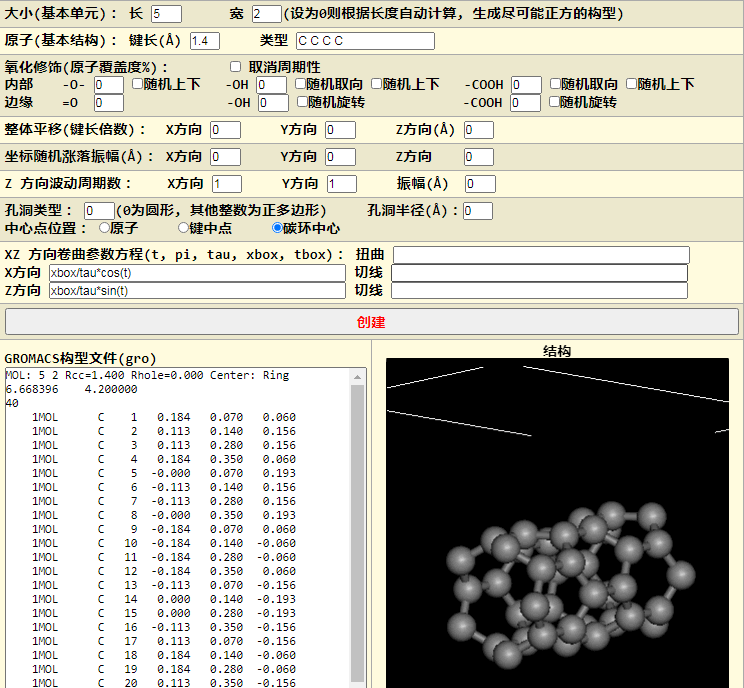
接下来试试简单的极坐标曲线, 阿基米德螺线
$$x=t\cos(t) \ z=t\sin(t)$$

有点意思, 但长度不够, 不明显. 增加盒子长度再试试
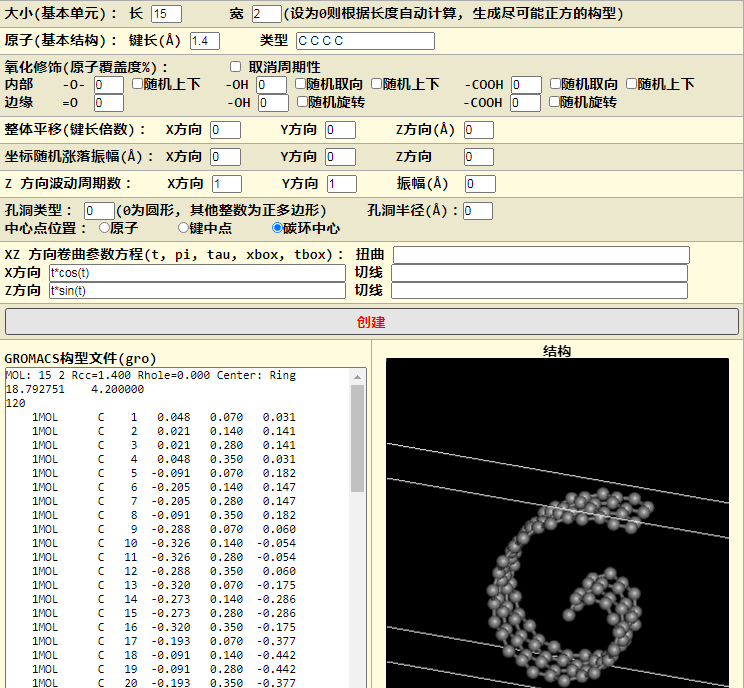
这个更6了吧.
心脏线行不行:
$$x=\cos(t)-.5\cos(2t) \ z=\sin(t)-.5\sin(2t)$$
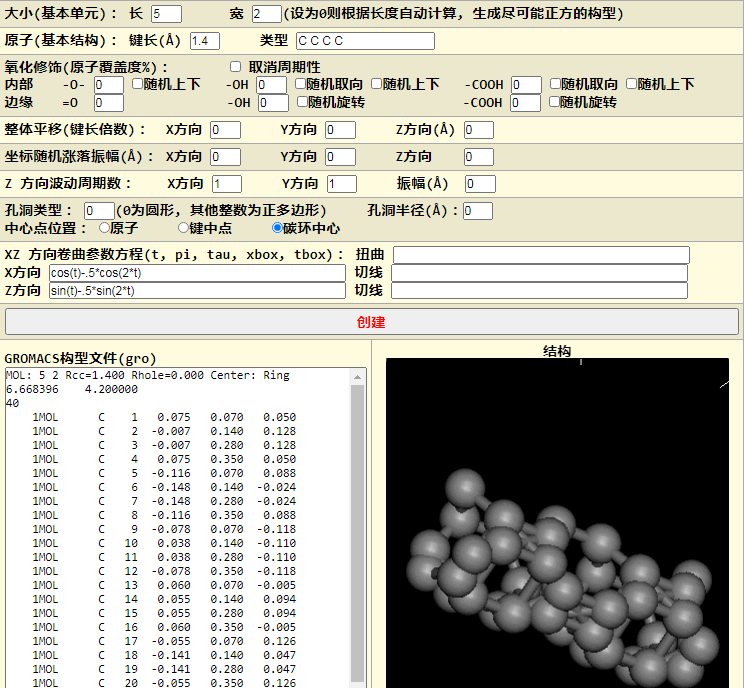
嗯, 与前面同样的问题, 半径过小. 让我们把半径变大
$$x=10(\cos(t)-.5\cos(2t)) \ z=10(\sin(t)-.5\sin(2t))$$
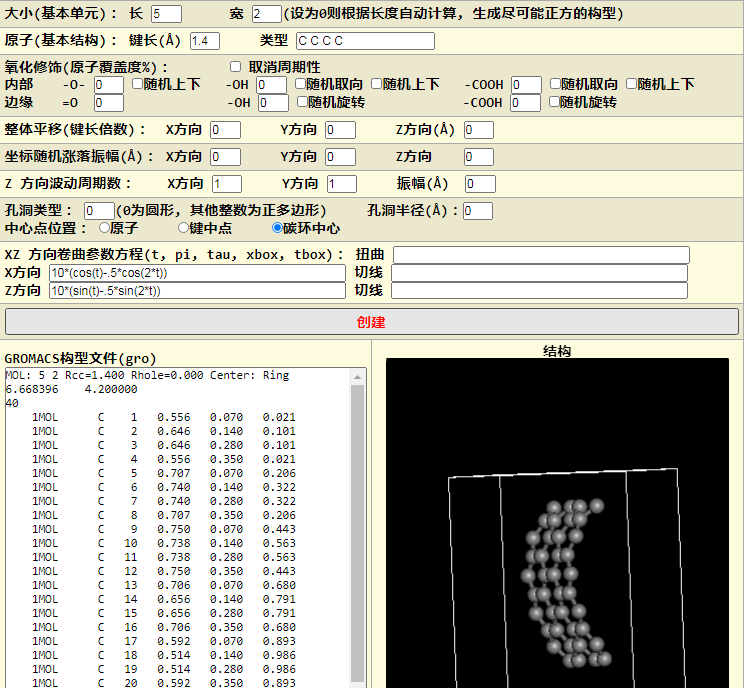
长度不够. 好像没有简单的办法确定到底该用多长, 就随便试试吧, 直到结果满意. 33好像差不多
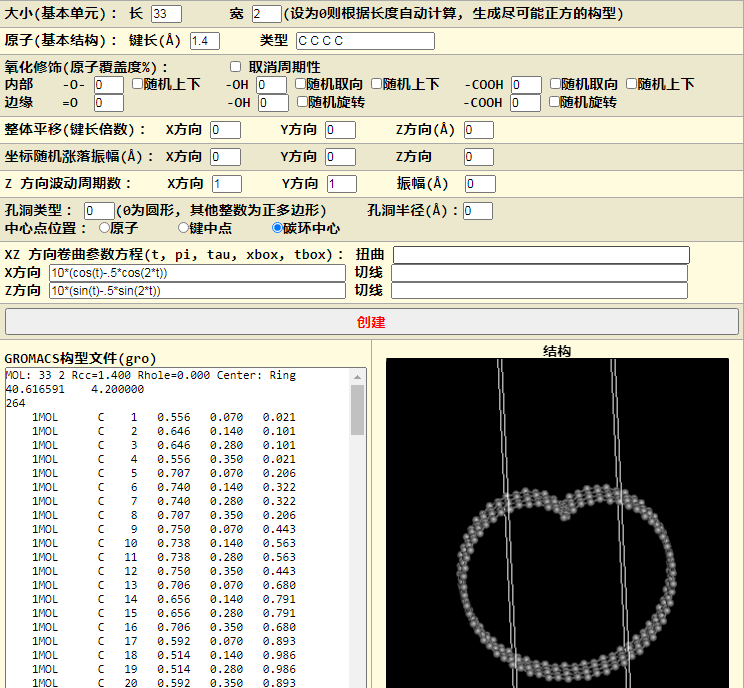
最后再试个更有趣爱心线, 同时变下色彩
$$\alg x &=16\text{pow}(\sin(t),3) \ z &=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4*t) \ealg$$
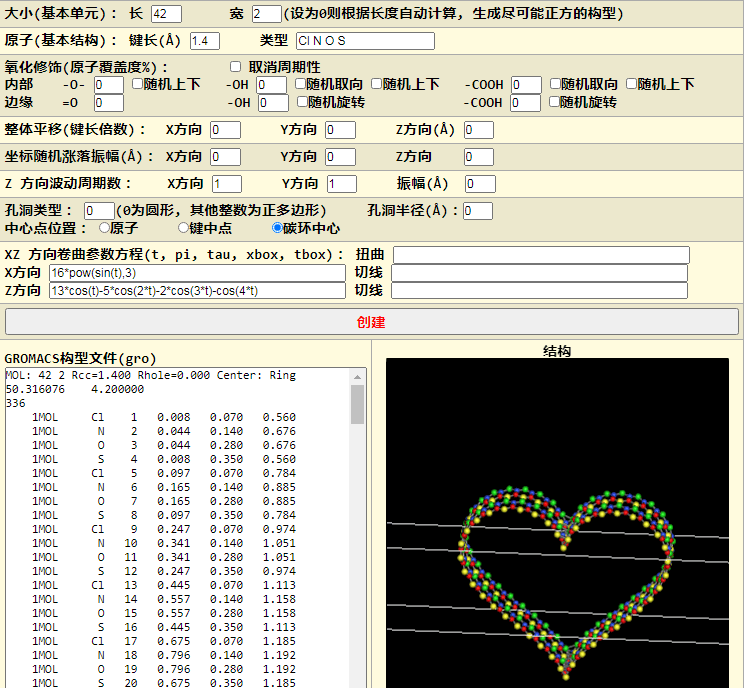
平面曲线无穷无尽, 你可到下面的链接找些有趣的自己试试.
我们已经能够将石墨烯平面卷曲各种形状了, 再进一步想, 能不能在卷曲的同时对平面进行扭曲呢? 有这个想法是因为考虑到一个特殊的曲面, 莫比乌斯面, 这是只有一个面的曲面. 我们能不能将石墨烯卷曲扭曲成这种曲面呢?
首先, 我们来看看莫比乌斯面的参数方程:
但是我们没有办法直接使用这个曲面的参数方程, 只得另想办法. 扭曲的本质是什么呢? 就是石墨烯平面的法向发生变化, 所以我们只要在卷曲的同时对平面法向进行改变就能达到扭曲的目的. 怎么做呢? 相对于目标曲线的切线方向旋转一定角度. 所以我们需要目标曲线切线的参数方程, 以及扭曲角度与参数 $t$ 的关系, 对应于扭曲的速率. 具体如何沿某个方向旋转, 这是一个常见的问题, 使用四元数矩阵很容易解决.
这些处理综合起来, 还是要写不少代码的. 如果你不明白这些背后的知识, 上来就看代码, 很难看明白.
为方便使用, 扭曲 方程中除了可以使用卷曲方程中的定义的几个常量, 还可以使用tbox常量, 对应于弧长为xbox时 $t$ 参数的值.
卷曲一周时扭曲180度就得到莫比乌斯面
$$t*\text{tau/tbox}$$
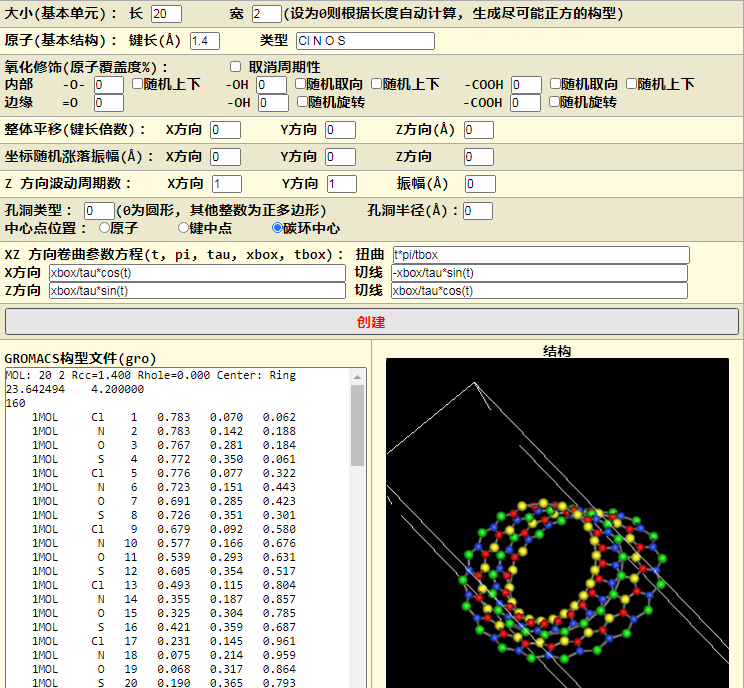
扭曲360度的莫比乌斯面
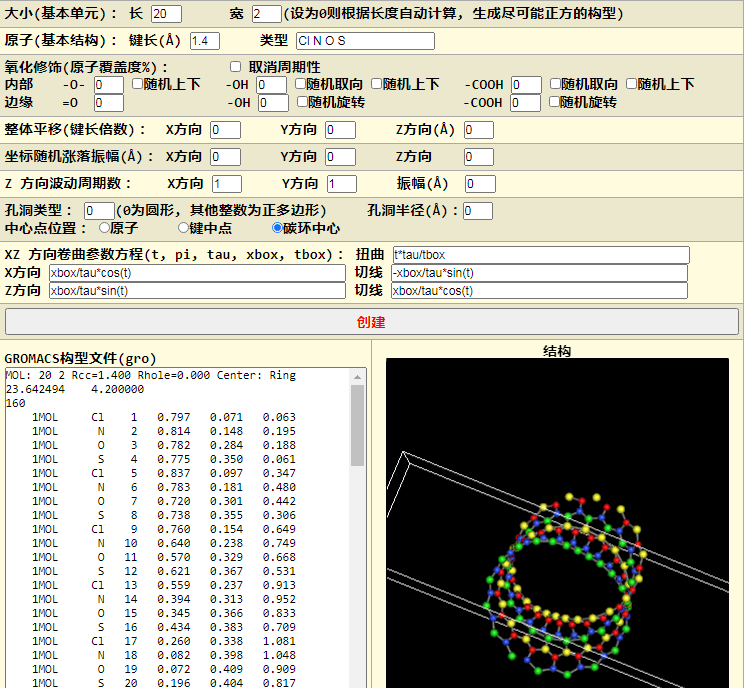
爱心曲线同样可以扭曲, 虽然这种说法不好听
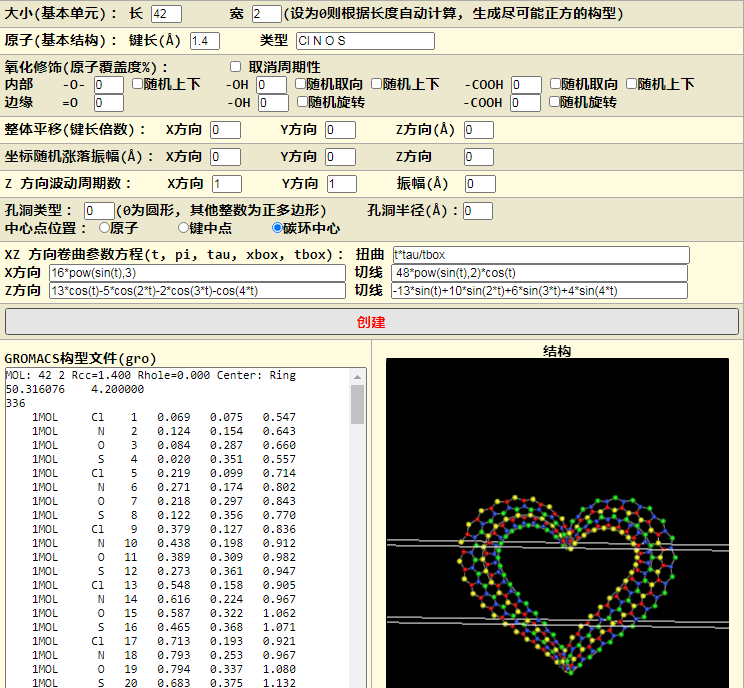
问题虽然解决了, 但是肯定还有未涉及的地方或者有待改进的地方: