layout: post title: 石墨烯：建模, 几何性质及力场模拟 categories:
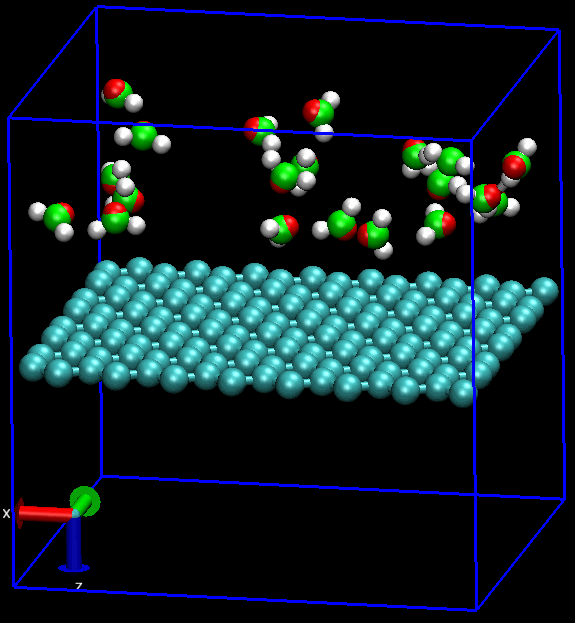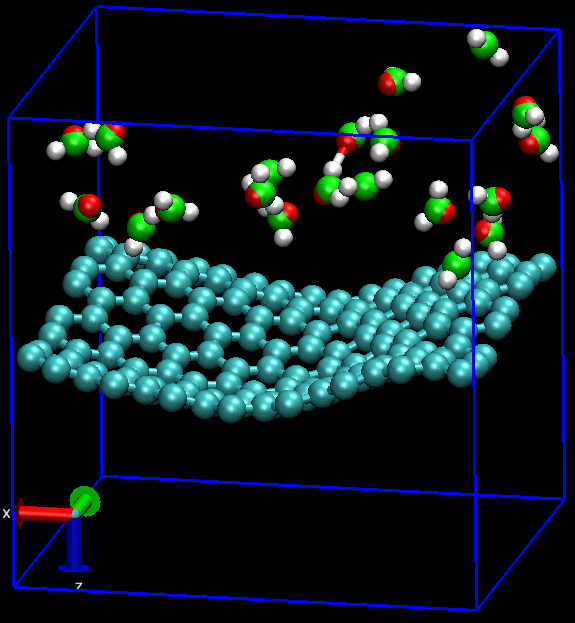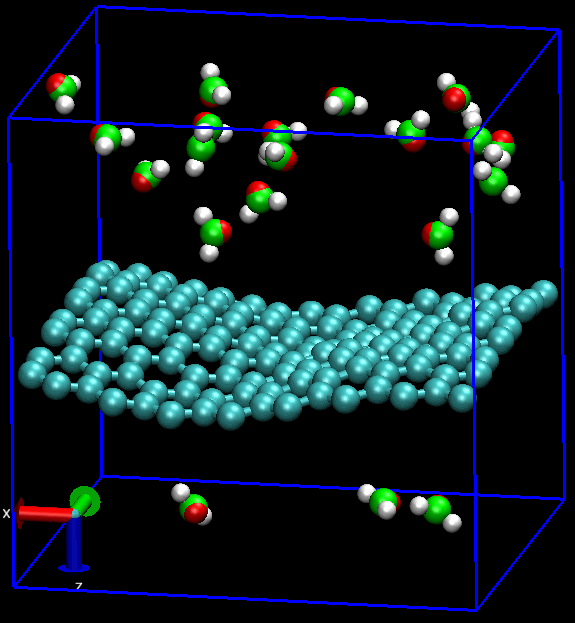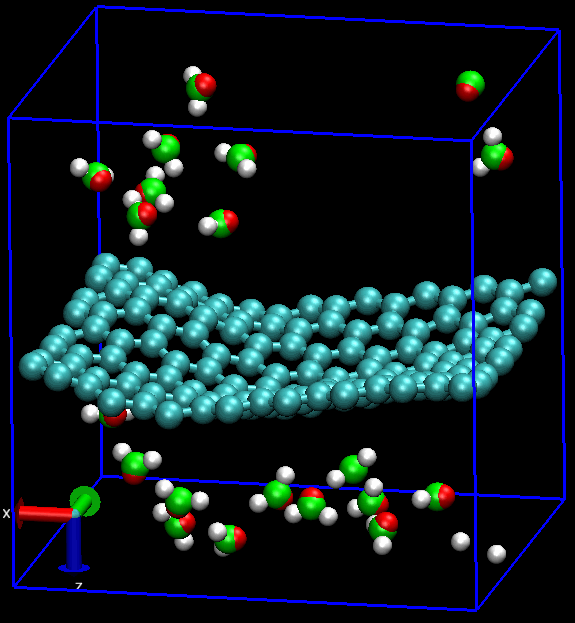
无论是做何种类型的计算研究, 首要的工作就是建模. 对分子动力学模拟MD而言, 还要加上体系的力场化, 明确指出体系中的各种相互作用. 石墨烯的MD也不例外.
只要熟悉晶体方面的知识, 石墨烯的建模不算复杂, 一种简单的方法可参考 建立石墨烯（Graphene）的模型. 这种方法构造出来的是六方结构, 用作MD不是很方便. 在六方结构上进行增删原子可得到四方结构, 但手动做起来有点麻烦. 所以还是写个简单的脚本来实现吧.
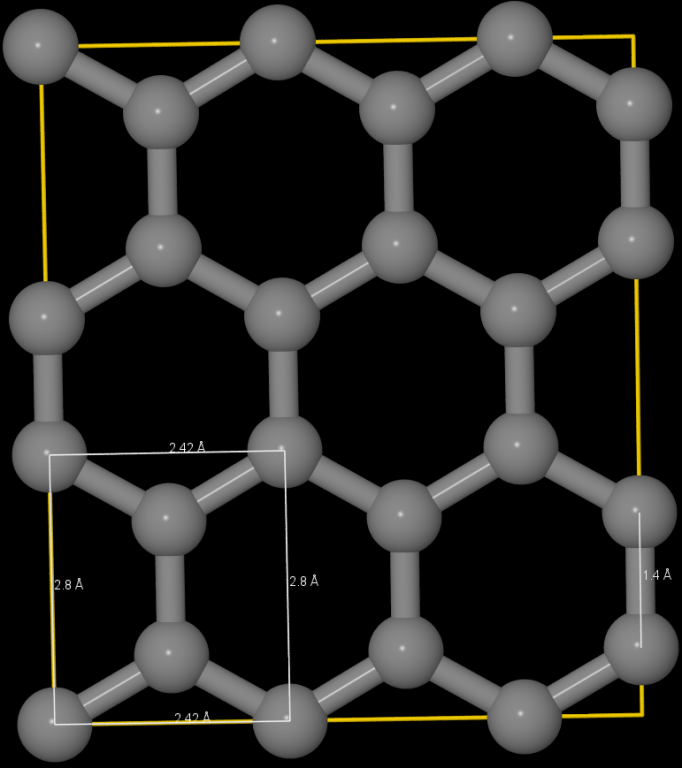
脚本实现的原理如下: 将石墨烯分解为含有四个C原子的基本单元, 再将基本单元在二维平面中排布.
若以C-C键长为单位, 基本单元的长宽分别为 $\sqrt 3, 3$, 其中的C原子坐标为 $(0,1/2) (0,5/2) (\sqrt 3/2, 1) (\sqrt 3/2, 2)$
力场化之前需要清楚石墨烯的几何性质, 主要是原子个数, 键数, 键角数, 二面角个数之间的关系.
<table><caption>石墨烯化学几何关系</caption> <tr> <th style="text-align:center;"> 化学 </th> <th style="text-align:center;"> 几何 </th> <th colspan="2" style="text-align:center;"> 数目 </th> </tr> <tr> <td style="text-align:center;"> 碳环数 </td> <td style="text-align:center;"> 六边形数 </td> <td colspan="2" style="text-align:center;"> 0.5N</td> </tr> <tr> <td style="text-align:center;"> 原子数 </td> <td style="text-align:center;"> 顶点数 V </td> <td colspan="2" style="text-align:center;"> N</td> </tr> <tr> <td style="text-align:center;"> 键数 </td> <td style="text-align:center;"> 棱数/边数E</td> <td colspan="2" style="text-align:center;"> 1.5N</td> </tr> <tr> <td style="text-align:center;"> 键角数 </td> <td style="text-align:center;"> 角数 </td> <td colspan="2" style="text-align:center;"> 3N</td> </tr> <tr> <td style="text-align:center;">二面角数 </td> <td style="text-align:center;"> </td> <td colspan="2" style="text-align:center;"> 6N</td> </tr> <tr> <td style="text-align:center;">1-3相邻数</td> <td style="text-align:center;"> </td> <td colspan="2" style="text-align:center;"> 3N</td> </tr> </table>数算方法
从拓扑角度来说, 对闭曲面, 其顶点数 $V$, 棱数 $E$, 面数 $F$ 与 欧拉示性数 $\c$ 和 亏格 $g, k$ 之间存在下面的关系
$$V-E+F=\c =\begin{cases} 2(1-g) &可定向曲面 \ \ 2-k &不可定向曲面 \end{cases}$$
石墨烯周期性体系与闭合的碳环面拓扑等价, 为可定向曲面, 其亏格 $g=1$, 因此 $V-E+F=0$.根据前面已知的关系
$F=E-V=V/2$
因此, 也可以根据六边形个数计算键数, 键角数和二面角数
periodic_molecules = yes选项, 否则计算有误.