上篇文章没有具体说明如何做颜色混合/融合, 因为我当时了解的也不多. 近几日看了一些资料, 知道的多了一些, 也就顺便记在这里吧.
处理颜色混合, 总免不了涉及颜色空间和颜色模型. 这是很大的话题, 我不是这方面的专家, 只略知自己用到的一些. 大致而言, 人眼中存在三类不同的细胞, 可以响应不同波长的光, 这些响应综合起来形成了人对颜色的感知, 所以人可以感知的颜色可以用三种颜色混合而成. 这样, 就可以用三个不同的分量来描述所有人可以感知的颜色. 因此, 各种颜色空间都是三维的, 用三个分量来表示颜色. 最常见的RGB颜色空间就是用红绿蓝三个分量来表示各种颜色的. 各种颜色空间都可以描述同样的颜色, 所以它们之间可以相互转换, 就像数学上的空间向量可以使用不同的坐标系描述, 具有不同的坐标分量, 这些分量之间可以相互转换. 在实际中具体使用哪个颜色空间, 取决于需要和方便程度, 这也是存在多种颜色空间的原因. 理论上, 有无穷多颜色空间, 它们都是等价的, 就像数学上存在无穷多的坐标系, 但常用的坐标系并不多一样, 常用的颜色空间也不是很多, 主要有:
上面这几种颜色空间都很老了, 近几年提出了几种比较重要的, 偏感知的颜色空间:
一般人可能会遇到的颜色空间基本就是这些了.
有些颜色空间会使用颜色强度分量, 其中比较好的是YUV, okLab这两种. HCT是谷歌刚刚推出的, 换算比较复杂, 实现麻烦, 效果即便好于okLab, 也有限, 所以暂且先不考虑了.
YUV颜色空间是一个统称, 有多种不同的变体, 如果名称中使用了Y'则表示颜色值已包含了伽马校正. 根据维基百科的说明, YUV有几种不同的标准, 标准的完整名称类似ITU-R Recommendation BT.2020, 有时会简写为Rec. BT.2020, Rec. 2020, BT.2020等. 在这些标准中, BT.609针对标清视频, BT.709针对HD高清视频, BT.2020针对超高清视频. BT.709的色域和sRGB大致相同, BT.2020的色域则大得多, 但目前用的还比较少, 因为很多显示器还不支持.
关于YUV和RGB之间的转换, 网上很多, 给出的公式也很乱:
下面根据维基给出的数据, 列出几种YUV标准与sRGB之间换算的详细计算过程, 用于对比/验证/确认公式.
BT.470标清
$$╤ W_R &= 0.299 \ W_G &=1-W_R-W_B=0.587 \ WB &= 0.114 \ U{\max} &= 0.436 \ V_{\max} &= 0.615 ╧$$
$$╤ Y' &= W_R R' +W_G G' +WB B' \ &= 0.299 R' +0.587 G' +0.114 B' \ U &= {U{\max} /1-WB} (B'-Y') \ &= {U{\max} /1-W_B} (B'-W_R R' -W_G G' -WB B') \ &= {U{\max} /1-W_B} (-W_R R' -W_G G' +(1-WB) B') \ &= { U{\max}/1-W_B} (-W_R R' -WG G') +U{\max} B' \ &= {0.436/0.886}(-0.299 R' -0.587 G') + 0.436B' \ &= 0.4920993227990971 ×(-0.299 R' -0.587 G') + 0.436B' \ &= -0.14713769751693 R' -0.28886230248307 G' + 0.436B' \ V &= {V_{\max} /1-WR} (R'-Y') \ &= {V{\max} /1-W_R} (R'-W_R R' -W_G G' -WB B') \ &= {V{\max} /1-W_R} ((1-W_R) R' -W_G G' -WB B') \ &= V{\max} R' + {V_{\max} /1-W_R} (-W_G G' -W_B B') \ &= 0.615 R' +{0.615/0.701}( -0.587 G'- 0.114B') \ &= 0.615 R' +0.877318116975749×( -0.587 G'- 0.114B') \ &= 0.615 R'- 0.5149857346647646 G' - 0.1000142653352354 B' ╧$$
BT.610标清
除$U{\max}$, $U{\max}$皆取0.5外, 与BT.470相同.
$$╤ W_R &= 0.299 \ W_G &=1-W_R-W_B=0.587 \ WB &= 0.114 \ U{\max} &= 0.5 \ V_{\max} &= 0.5 ╧$$
BT.709高清
$$╤ W_R &= 0.2126 \ W_G &=1-W_R-W_B=0.7152 \ WB &= 0.0722 \ U{\max} &= 0.436 \ V_{\max} &= 0.615 ╧$$
$$╤ Y' &= W_R R' +W_G G' +WB B' \ &= 0.2126 R' +0.7152 G' +0.0722 B' \ U &= {U{\max} /1-WB} (B'-Y') \ &= {U{\max} /1-W_B} (B'-W_R R' -W_G G' -WB B') \ &= {U{\max} /1-W_B} (-W_R R' -W_G G' +(1-WB) B') \ &= { U{\max}/1-W_B} (-W_R R' -WG G') +U{\max} B' \ &= {0.436/0.9278}(-0.2126 R' -0.7152 G') + 0.436B' \ &= 0.4699288639793059 ×(-0.2126 R' -0.7152 G') + 0.436B' \ &= -0.09990687648200043 R' -0.3360931235179995 G' + 0.436B' \ V &= {V_{\max} /1-WR} (R'-Y') \ &= {V{\max} /1-W_R} (R'-W_R R' -W_G G' -WB B') \ &= {V{\max} /1-W_R} ((1-W_R) R' -W_G G' -WB B') \ &= V{\max} R' + {V_{\max} /1-W_R} (-W_G G' -W_B B') \ &= 0.615 R' +{0.615/0.7874}( -0.7152 G' -0.0722 B') \ &= 0.615 R' +0.7810515621031242×(-0.7152 G' -0.0722 B') \ &= 0.615 R' - 0.5586080772161544 G' - 0.05639192278384557 B' ╧$$
BT.2020超高清
$$╤ W_R &= 0.2627 \ W_G &=1-W_R-W_B=0.678 \ WB &= 0.0593 \ U{\max} &= 0.436 \ V_{\max} &= 0.615 ╧$$
上面所给的是精确换算公式, 实际应用中为加快处理速度会根据情况进行一定的近似, 如使用整数运算代替浮点数运算, 使用位运算加快计算速度, 对取值范围进行调整等. 所以很多文章中所给的具体数字经常会不同, 在使用前需要确认是否正确. .
okLab颜色空间的换算公式, 直接看其作者给出的代码即可. 但具体数字似乎有点小问题, 我没有验证.
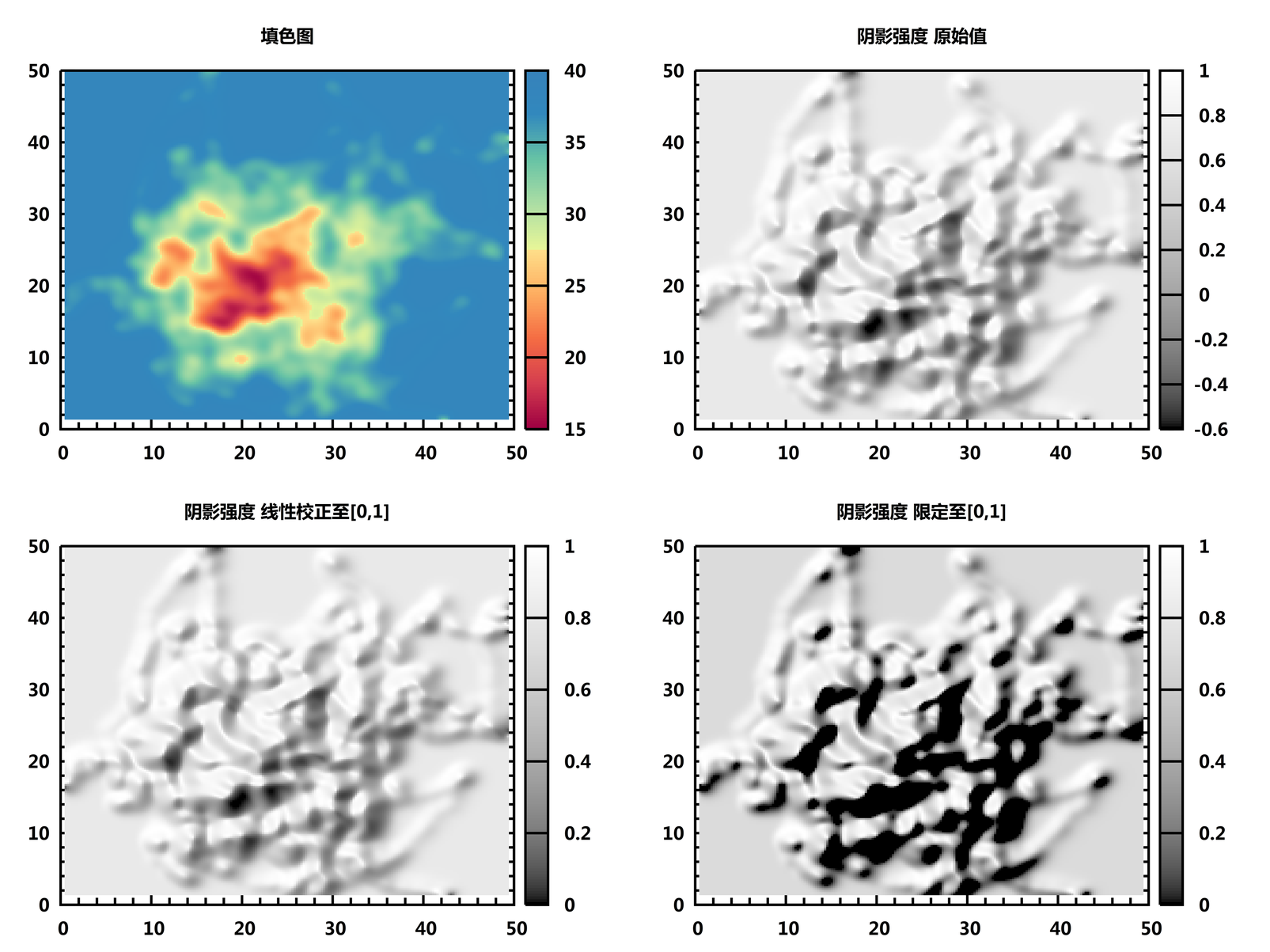
计算山体阴影强度时, 有时会出现负值. 处理这些负值时至少可以采用两种不同的方法, 一种是将所得阴影强度线性标定至[0,1]范围内, 一种是直接将强度限定在[0,1]范围内.
将阴影强度与颜填色图混合时可能有多种不同的方法, 粗略地可分为相乘, 相加两类. 前者将阴影强度视为颜色强度, 后者则采用类似透明度的模式叠加. 再细分下去, 还有很多细节的不同, 颜色强度如使选, 在哪个颜色空间进行混合等. 这些都涉及人的感觉, 但人的感觉并不是很精确, 也就无法确定怎么做是最好的, 最后只能诉诸艺术了.
使用上一篇文章中的自由能数据, 先看看原始数据以及不同方法处理后的阴影数据

下面分别使用不同方法来绘制颜色混合图
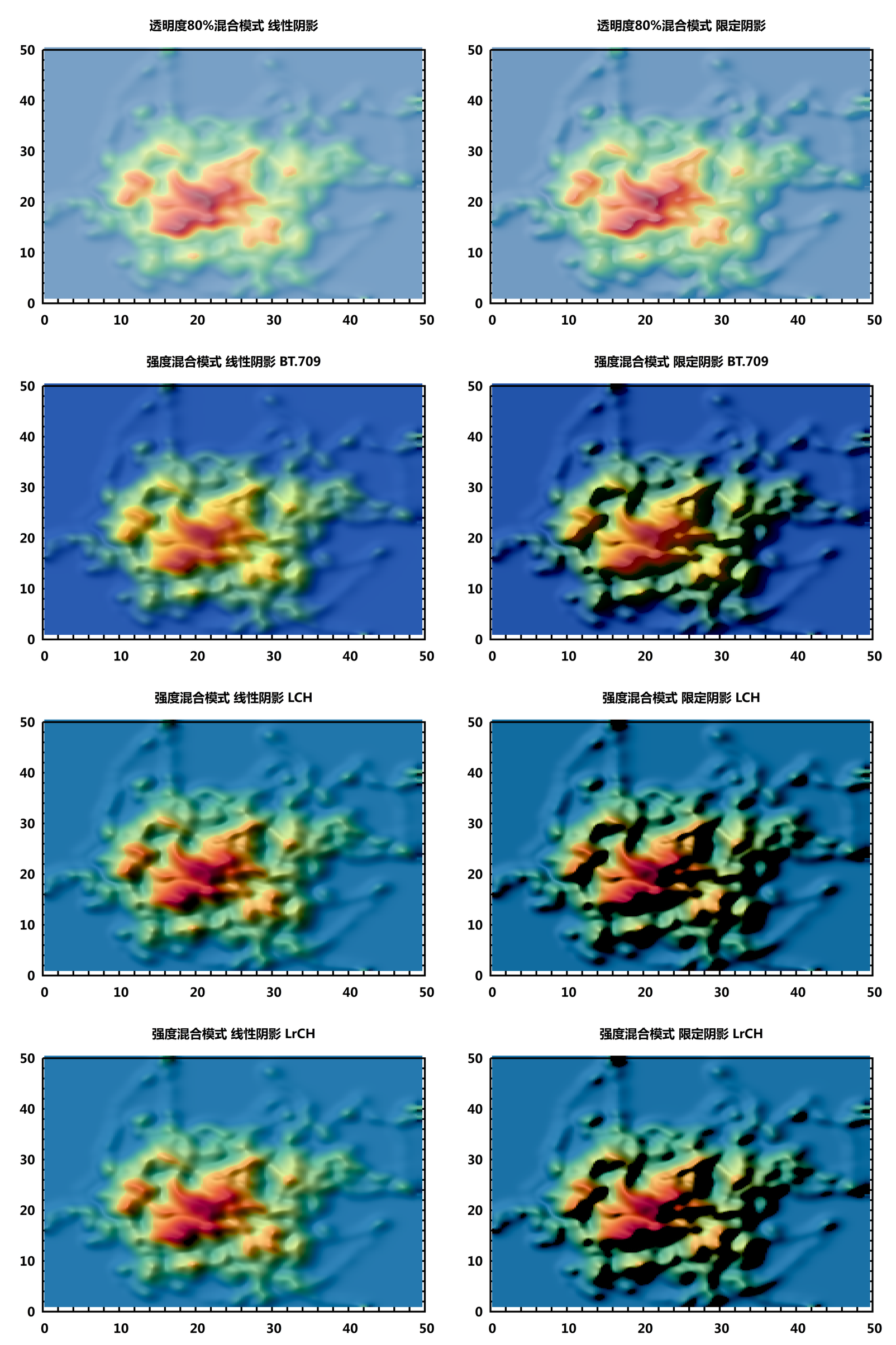
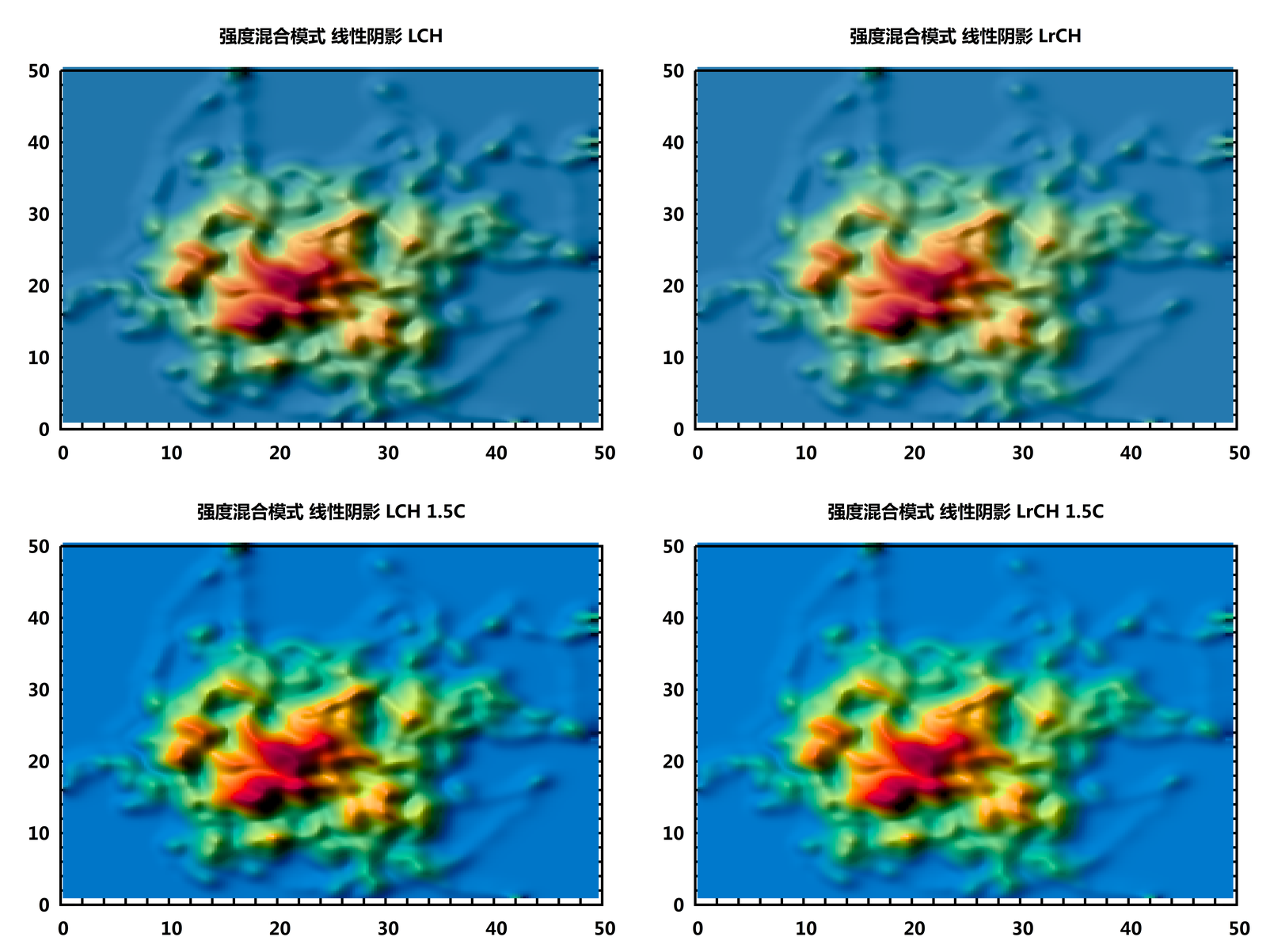
看起来, 使用强度混合模式, 线性阴影, LrCH效果更好. 使用这种颜色空间的另一个优点在于可以比较容易地调整颜色的亮度. 下面的图是将C变为原来1.5倍后的对比.