The following is my notes about the GROMACS Soft-Core Potential for Free Energy Calculation
The soft-core potential between two states A and B is defined as
$\begin{split} V_{sc}(r) &=(1-\lambda)V_A(r_A) + \lambda V_B(r_B) \ &=(1-\lambda)V_A(r) + \lambda V_B(r) \;\;\;\; \text{if } \alpha \sigma=0 \ r_A &= \left(\alpha \sigma_A^6 \lambda^p+r^6\right)^{1/6} \ r_B &= \left(\alpha \sigma_B^6 (1-\lambda)^p+r^6\right)^{1/6} \ \end{split}$
When $\alpha=0$ or $\sigma=0$, the soft-core potential degenerates to the original potential. $\alpha$ is usually about 0.5 and $p=1$ or $p=2$. The recommended combination is $\alpha=0.5, p=1$.
For LJ potential,
$\alg V &= { C_{12} \over r^{12} } - {C6 \over r^6} \ V{sc} &=C_{12}\left[{1-\lambda \over (\alpha \sigma^6 \lambda^p+r^6)^2} + {\lambda \over (\alpha \sigma^6(1-\lambda)^6+r^6)^2}\right] \ &-C_6 \left[{1-\lambda \over \alpha \sigma^6 \lambda^p+r^6} + {\lambda \over \alpha \sigma^6(1-\lambda)^6+r^6}\right] \ealg$
Some special cases
$\alg V_{sc}=0 &\Rightarrow V(r_A)=0 \; V(r_B)=0 \ r_A=r_B &\Rightarrow \lambda=0.5 \ealg$
If A state is totally decoupled, which means $V_A=0$, in this case
$\alg V_{sc}(r) &= \lambda V_B(rB) \ &= \lambda \left\{ {C{12} \over \left(\alpha \sigma^6 (1-\lambda)^p+r^6\right)^2} -{C_6 \over \alpha \sigma^6 (1-\lambda)^p+r^6} \right\} \ealg$
Define
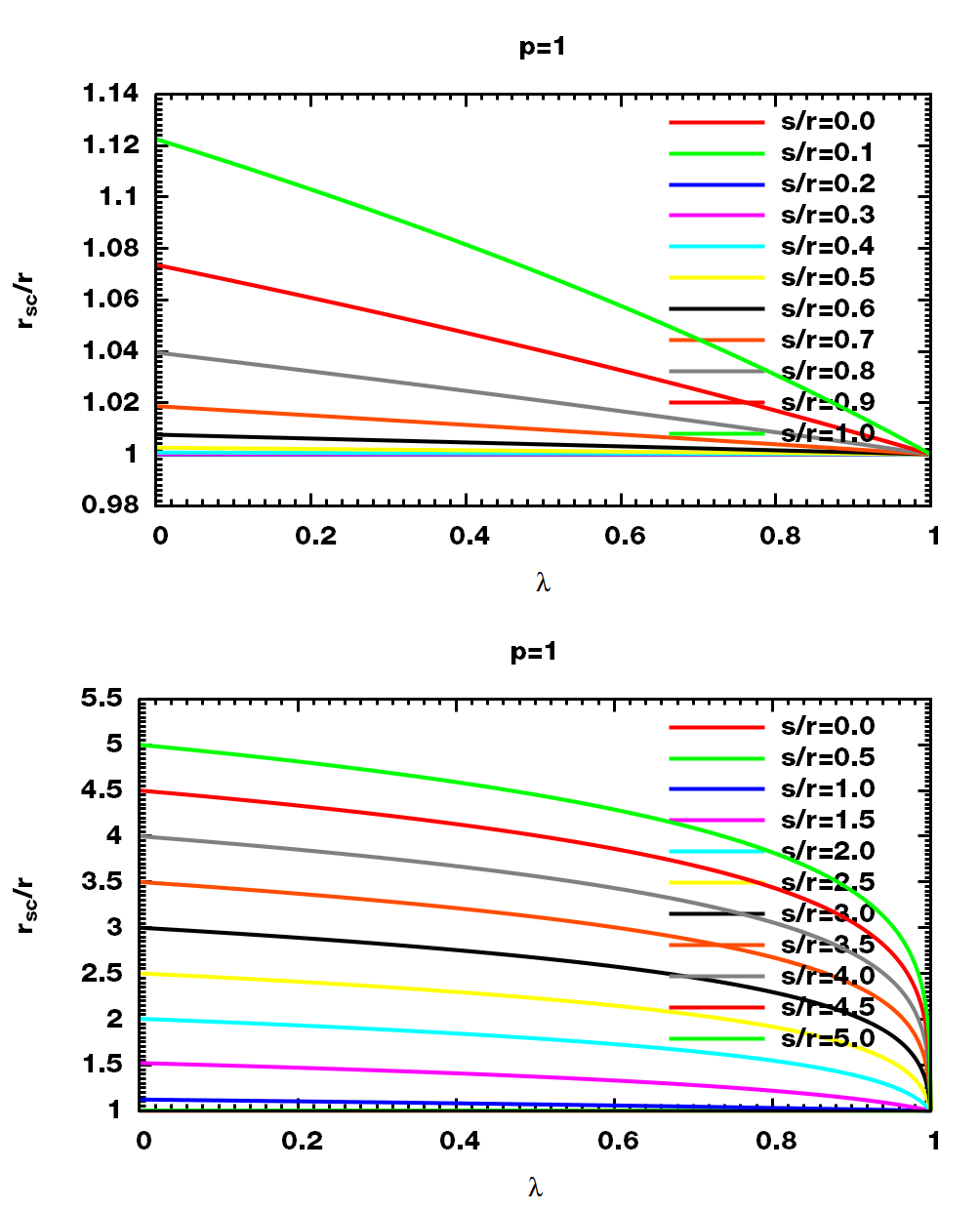
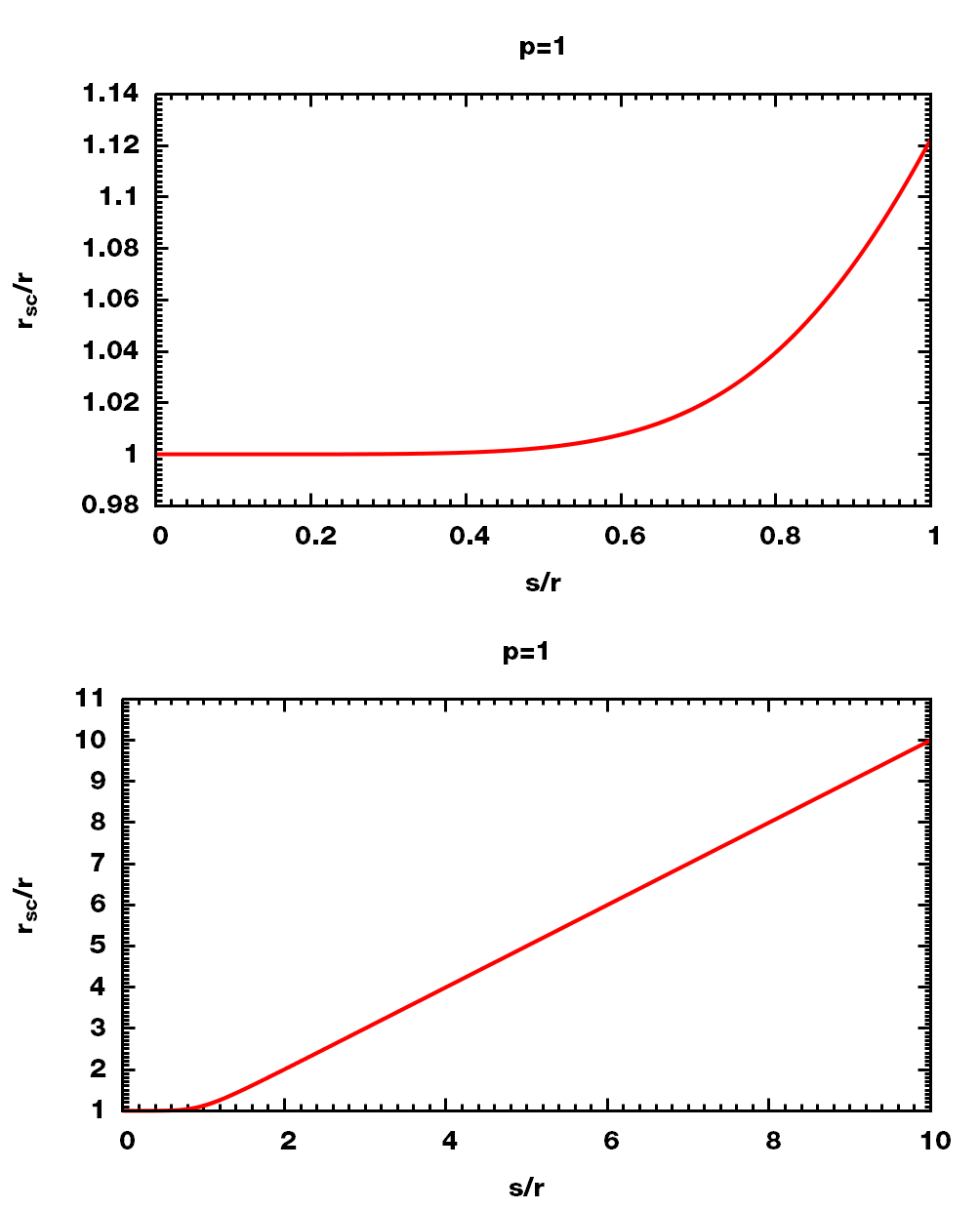
$\alg s^6 &=\alpha\sigma^6 \ r{sc} &= \left(r^6+ (1-\lambda)^p s^6\right)^{1/6} \ \min r{sc} &= r &\;\; \text{when } \lambda=1 \ \max r_{sc} &= (r^6+s^6)^{1/6} &\;\; \text{when } \lambda=0 \ealg$
$$r_{sc}/r = \left(1+(1-\lambda)^p (s/r)^6\right)^{1/6}$$

$$\max r_{sc}/r = (1+(s/r)^6)^{1/6}$$
$$\alg V{sc}(r, s, \l) &= \lambda \left\{ {C{12} \over \left(r^6+(1-\lambda)^p s^6\right)^2} -{C_6 \over r^6+(1-\lambda)^p s^6} \right\} \ &=4\e \lambda \left\{ {\s^{12} \over \left(r^6+(1-\lambda)^p s^6\right)^2} -{\s^6 \over r^6+(1-\lambda)^p s^6} \right\} \ealg$$
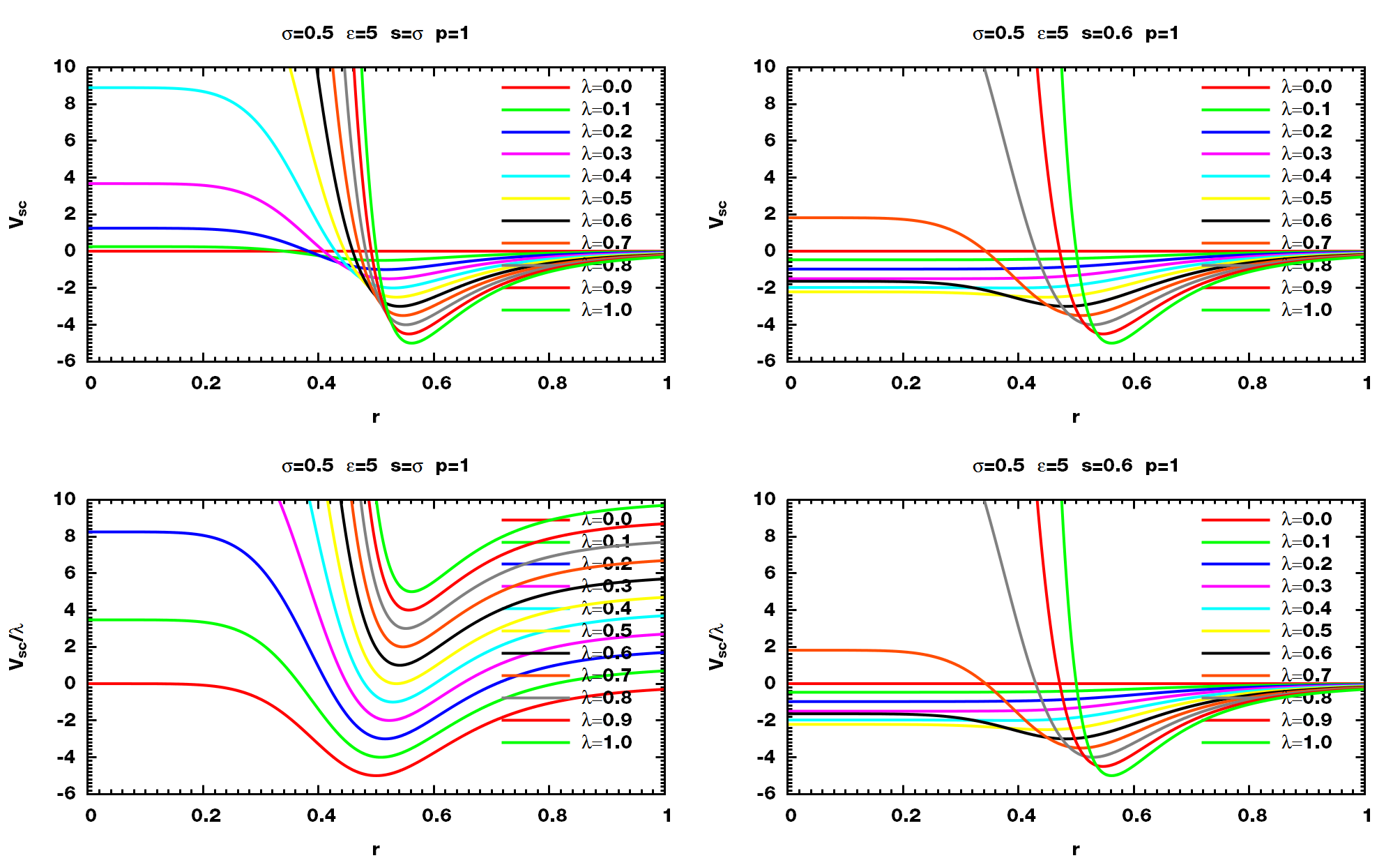
In GMX, $\alpha, \sigma, p$ is corresponding to sc_alpha, sc_sigma, sc_power, respectively.
The manual said
sc-alpha: (0)
the soft-core alpha parameter, a value of 0 results in linear interpolation of the LJ and Coulomb interactions
sc-r-power: (6)
the power of the radial term in the soft-core equation. Possible values are 6 and 48. 6 is more standard, and is the default. When 48 is used, then sc-alpha should generally be much lower (between 0.001 and 0.003).
sc-power: (0)
the power for lambda in the soft-core function, only the values 1 and 2 are supported
sc-sigma: (0.3) [nm]
the soft-core sigma for particles which have a C6 or C12 parameter equal to zero or <font color="#FF0000">a sigma smaller than sc-sigma</font>
The description of sc-sigma is not correct, actually
$\sigma= \begin{cases} & \sigma^*=(C{12}/C{6})^{1/6} \ & \text{sc_sigma} \; \text{ if } C6\times C{12}=0 \end{cases}$
See the discussion
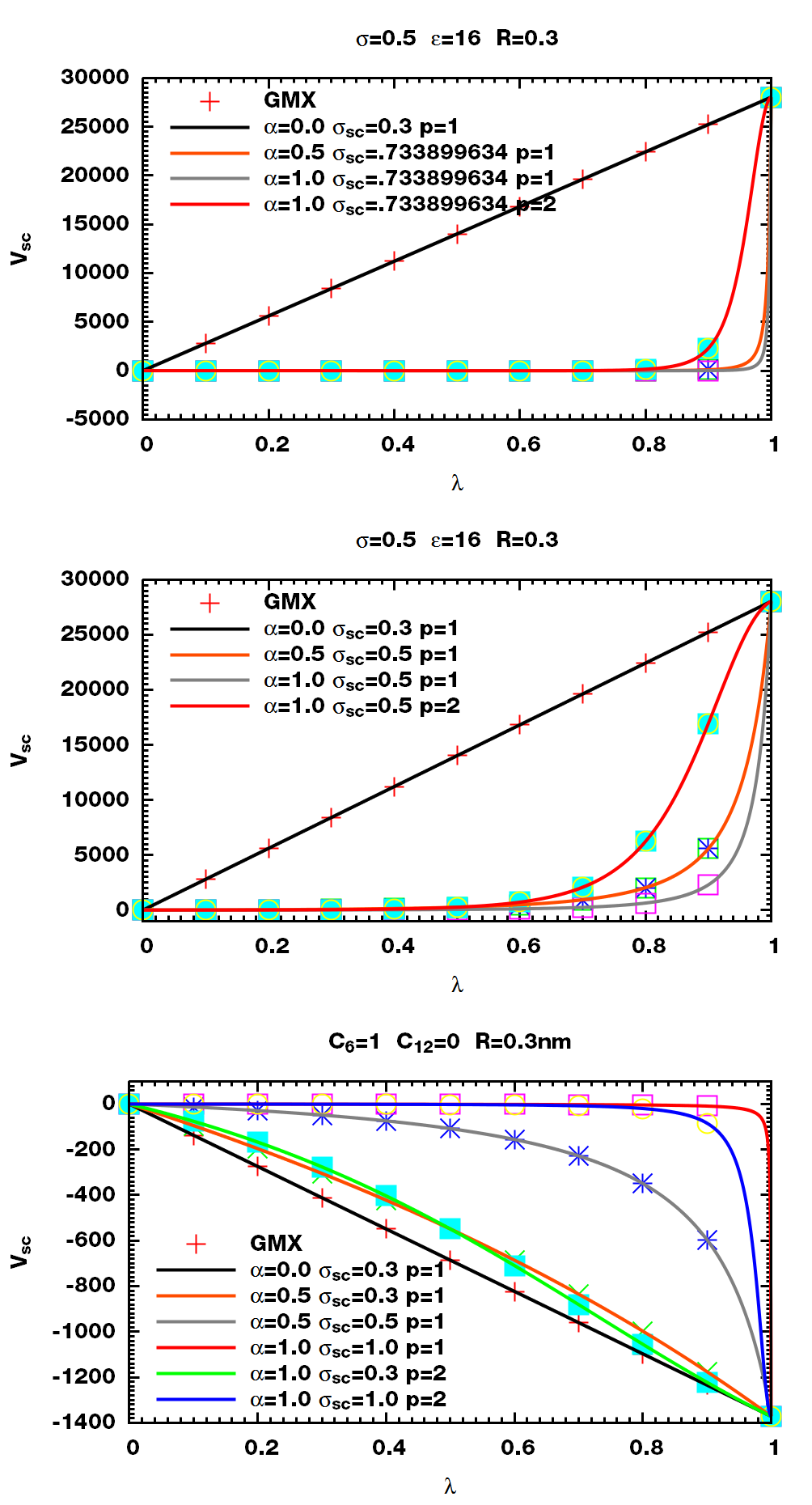
GROMACS DOES support table potential for free energy calculations
GROMACS calculates the interaction only If r_sc less than rvdw
The r_sc for any distance should be in the range of the table files, otherwise GROMACS will use a unkown value
If DispCorr is used, be sure C6 is the correct value
If sc-alpha is not zero, be sure the $\s$ GROMACS used is the correct value
If DispCorr not used, put total interaction in dispersion or repulsion column will force GROMACS to use sc-sigma
If DispCorr is used and sc-alpha is not zero, be sure C6 and C12 are both correct