
聚合物的参数化与其他分子参数化的标准过程基本一致, 但是仍有一些因素需要考虑.
有时, 你想要自己的聚合物模型能再现某些来自实验或全原子模拟的特定性质, 例如, 回转半径或是螺旋倾向. 与简单分子的参数化相比, 这些性质更加依赖于键/非键相互作用. 试着在拟合时考虑更大范围内距离和角度的分布, 并理解哪些因素可能导致粗粒化聚合物偏离这些性质.
在处理低聚物时, 末端残基的行为往往不能代表分子其余残基的行为. 对足够长的聚合物链中的中心残基来说, 其行为具有一致性, 因为从它们获取参考分布是较好的做法. 如果末端残基的行为非常不同, 可能需要为它们指定另一套不同的势能函数.
你可能会发现, 无论使用多少势函数, 或者映射得多精细, Martini仍然不能如实地再现你想要的长程结构组织. 在你放弃之前, 你可以使用弹性网络将珠子约束到你想要的构象(参见蛋白质的例子). 网络的柔性是可调的, 也许足够满足你的需要.
一些聚合物中可能存在取决于构象的, 不同的分子内偶极作用或盐桥(想想蛋白质中的羧基酰胺氢键). 一组单一的珠子类型也许不足以描述聚合物所有构象的有效极性. 这需要对每一构象指定中骨架珠子的极性取决于它们的二级结构. 注意这样的指定是静态的, 在模拟中即便构象变化指定也不会改变. 因此这种方法在聚合物构象确定保持不变时最有用(例如, 当使用弹性网络约束它时).
在聚合物熔体的情况下——或者甚至当使用小分子溶剂时——获得正确的密度变得至关重要. 迭代参数化步骤中应该考虑这一点.
当对长度以及残基组分有变化的聚合物进行参数化时. 分配行为的匹配最好基于单一残基/片段, 而不是整个分子. 这样才能得到最具有可移植性的行为.
在这个教程中我们根据目标全原子数据对PEG9进行Martini参数化. 重点在匹配键合构象的映射分布, 以及平均密度和分子的回转半径. 目前. 珠子的指定仅仅匹配Martini的构筑模块——没有为匹配分配性质而进行修正.
这次练习将涉及一些GROMACS工具和脚本的使用(提供示例脚本, 但注意这些脚本只针对这个教程, 不经修改的话对其他分子的参数化很可能不适用). 我们将处理新分子参数化所面临的一些普遍问题, 以及与聚合物有关的一些特殊问题. 快速阅读一下分子参数化的教程非常有用(特别是其中的流程图), 因为它囊括了大部分通用的Martini参数化工作流程. 最后在本教程中我们建议了一些文件名, 但它们并不是固定的. 每个用户都可以自由地修改这些名字以适合自己的组织方式.
PEG的Martini模型已经发布(参见Lee等人的论文或更新的Rossi等人的论文). 本教程的目的不是对论文的补充, 而是提供一个参数化工作流程的例子. 基于同样的原因, 拓扑自动生成工具ATB用于产生目标原子数据就足够了.
我们从要参数化体系的目标原子轨迹开始. 在PEG_parametrization.tgz文件中, 你会发现AA目录下有200个PEG9熔体的100 ns轨迹. 这些数据是从PEG9的拓扑获得的, 这一拓扑是通过基于GROMOS 54a7联合原子力场的自动拓扑生成器得到的. 文件名为PEG9.itp(命名和原子顺序相比于ATB数据库的.itp稍有改变, 但是势函数没有变化). 一定要看一下.itp文件, 对分子中的原子顺序和命名有所了解.

图 1: AA聚合物熔体的不同查看方式. 左: 近100 ns模拟后的体系快照; 右: 与左边相同时间点附近, 时间平均(200 ps)的系综.
有了全原子的数据, 就可以决定全原子到粗粒的映射了. 每个乙烯乙二醇残基包含两个亚甲基和一个醚氧(在来自联合原子拓扑的目标数据中, 每个亚甲基用一个粒子表示). 一种合理的映射方案是为每个残基指定一个粗粒化珠子. 这种3对1的映射比Martini典型的4对1映射更精细. 或者, 两个残基指定为一个珠子, 6对1的映射. 图2展示了PEG不同的可能映射方案. 注意到在第一种映射中每个珠子对应O-C-C序列, 末端的指定不对称. 考虑到聚合物内在的对称性, 这是不合理的.
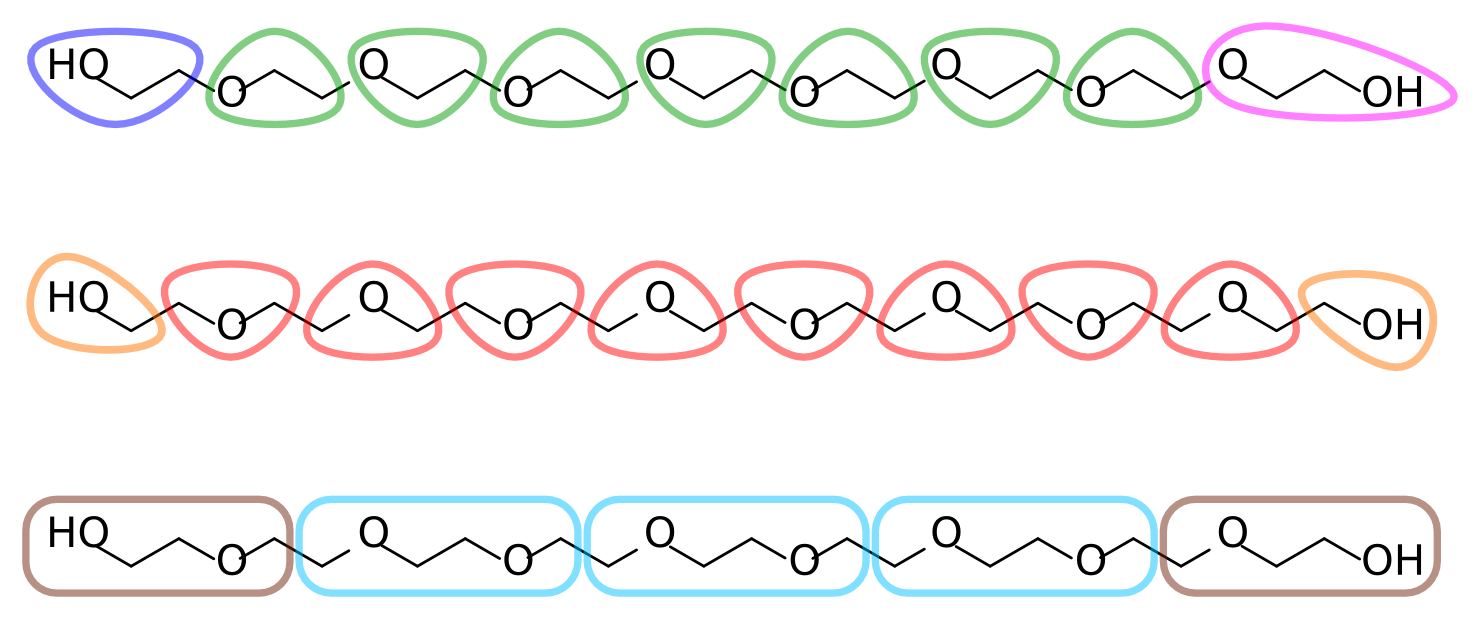
图2: PEG9不同的映射方案
本教程的其余部分使用图2中的第二种映射方案, 每个珠子代表C-O-C序列, 末端指定更小但对称的C-O-H. 自由地根据你的化学直觉来选择不同的映射, 这样更具挑战性和潜在的乐趣, 因为你将不得不更多地修改我们所提供的工具和文件.
使用选择的映射我们就可以将全原子坐标转换为粗粒化的坐标, 简单地将粗粒化珠子的坐标取为每组原子的质心即可. 有几种不同的方法进行这种所谓的"正向映射".
第一种方法使用GROMACS工具g_traj输出任意选区随时间变化的质心轨迹. 这需要创建一个索引文件, 其中包含每个珠子所代表的组, 每个组中分别列出全原子的原子编号. 可以想象, 像我们这样的体系需要编写许多脚本来准备这个索引文件, 因为有2000个组(或者与你映射产生的粗粒化珠子一样多). 脚本indexer.py将为你之执行此操作, 但是请编辑它以了理解其工作原理, 并确保其参数对于你选择的映射是正确的. 要使用g_traj, 需要2000个组, 设置-com选项, 并将其指向PBC处理过的全原子轨迹, 编译好的拓扑, 以及我们刚刚准备好的索引文件:
seq 0 1999 | g_traj -f AA/trajpbc.xtc -s AA/topol.tpr -oxt traj_cg.xtc -n mapping.ndx -com -ng 2000 -b 20000
g_traj将提示你哪些索引组对应于使用-ng请求的2000个组. 通过将seq 0 1999的输出使用管道传递给g_traj, 我们自动化了操作, 并确保它们的输出顺序正确. 这里我们还使用-b选项忽略作为预平衡的前20 ns轨迹. g_traj产生一个.xtc轨迹文件. 为了作为以后粗粒化模拟的起点, 以及可视化和分析的目的, 产生一个.gro文件很有必要. 可以对g_traj命令进行调整, 使用-b 100000来选择最后一帧, 并选择输出文件适当的扩展名:
seq 0 1999 | g_traj -f AA/trajpbc.xtc -s AA/topol.tpr -oxt cg.gro -n mapping.ndx -com -ng 2000 -b 100000
第二种正向映射方法使用backward工具, 我们在这里不详细讨论. 这个脚本是用于自动将粗粒化结构反向映射转换成全原子结构的, 但也可以执行正向映射. 它使用映射文件来决定根据哪些原子计算质心, 因此比上面的方法更灵活. 当处理具有不同残基的任意序列的聚合物时, 这一脚本更加有用, 因为编写创建索引的脚本并不简单.

图3: 质心映射后的全原子聚合物熔体的不同查看模式. 红色球代表质心, 深灰色代表键. 与图1的设置相同
有了映射的.xtc和.gro文件, 你现在可以使用g_bond和g_angle提取相关珠子的键合分布. 为此, 必须创建索引文件, 指定要测量的键/角/二面角(请参阅每个命令的-h选项). 同样, 生成成千上万的原子对(用于键), 三元组(用于角度)或四元组(用于二面角)需要编写一些脚本, 我们为你提供了gen_indices.py脚本. 如果检查代码, 你会注意到索引被分割在_core和_term组之间. 这些组将涉及末端的键合相互作用与仅涉及核心珠子的键合相互作用分割开来. 可能需要这么做, 因为 a) 末端与分子其余部分的映射方式不同, b) 即使它们跟核心珠子一样映射, 末端常常涉及不同或更极端的键合构型.
现在使用每个分析工具对每个索引组进行分析; 记住在选择末端和核心组时要更改输出文件名, 以免覆盖掉之前的结果:
g_bond -f traj_cg.xtc -blen 0.35 -tol 0.8 -n bonds.ndx -o bonds.xvg
g_angle -n angles.ndx -f traj_cg.xtc -od angdist.xvg
g_angle -type dihedral -n dihedrals.ndx -f traj_cg.xtc -od dihdist.xvg
稍后当你尝试再现这些分布时, 你将反复运行相同的命令. bash脚本calc_dists.sh会为你做这件事; 只要确保适当的文件名和位置.
现在查看你获得的分布. 将末端珠子与核心珠子进行比较, 并决定哪些应该考虑使用不同的势函数, 哪些可以同等对待. 你还可以据此预测那些重现可能存在问题的分布:
这时, 计算原子体系的密度也是一个好主意, 因为我们也需要匹配它(你也可以尝试匹配已知的实验密度, 如果你有的话). 如果有.edr文件可用, 可以使用g_energy工具来完成此任务. 然而, 如果没有.edr文件, 可以简单地使用
g_traj -f traj_cg.xtc -ob box.xvg -s cg.gro
此命令将提取随时间变化的盒向量. 然后可以使用g_analyze对其进行平均:
g_analyze -f box.xvg
可以从前三个平均值(分别对应于以nm为单位的X, Y和Z方向盒子的平均尺寸)计算平均体积. 根据平均体积, 就可以计算出体系的平均密度.
作为一个附加的参数化目标, 我们将重现原子化PEG分子的回转半径. 你可以使用g_polystat工具来计算它, 但需要一个.tpr文件来确定每个分子的原子数. 最好的是现在略过它, 当你得到一个包含合适的分子信息的粗粒度.tpr文件以后再计算它.
.itp文件对于这一步, 使用预先存在分子的.itp作为你自己分子的模板可能会有帮助(可以从Martini网站的一些可用的中选择). 因为在迭代优化过程中涉及这个文件的一些修改, 将它放在一个子目录运行是明智的(take0似乎是一个不错的名称). 当生成新的轨迹和分布文件时这会避免与全原子的或其他迭代的文件混淆. 本教程假设你将在每个take子目录中工作.
在[ moleculetype ]指令下, 应输入分子的名称. 这个名称是你在.top文件中引用的名称. 名称后面是排除非键相互作用时键合近邻的默认数量. 标准Martini流程将此值设置为1, 仅仅排除第一个键合近邻. 如果需要更多的排除, 通常最好在拓扑中单独添加它们.
此指令定义分子的原子属性. 记住, 在我们的粗粒化体系中, 分子具有10个原子(珠子). 此时, 原子和残基命名不太重要(但记住, 5个字符限制). 然而, 原子 类型 控制非键相互作用, 并且是粗粒化过程的核心部分. 同样, 你将使用你的化学直觉和2007年的Martini论文, 以判断哪个类型的珠子能更好地代表每个映射部分: 在论文中找到表3, 在那里找到与每个珠子最匹配的构建单元. 对于C-O-C映射, 可能是N珠子类型之一, 而对于末端, 则是P其中一个. 正确的选择意味着珠子与不同溶剂的相互作用遵循正确的分配能量(参见论文表格中用于参数化的溶剂). Martini背后的设想是, 通过匹配这些分配行为, 我们可以得到表中的珠子类型之间一致的非键相互作用强度.
Martini还提供了所谓的S珠子(SP, SN等). 它们比常规的珠子更小, 可以堆积得更紧密, 但具有更浅的非键势阱以防止固化. 它们通常用于比1对4更精细的映射, 并且在我们的情况下可能是有用的, 如果体系的密度太低的话. 请注意, 这些珠子只能更靠近其他S珠子, 与常规珠子间的相互作用遵循与常规珠子之间相同的势函数.
对于[ atoms ]指令的其余部分, 确保将所有珠子的电荷设置为0.0, 并且将它们指定为单独的电荷组. 将质量留空设为默认值. 当粗粒化时, 我们的键合参数旨在再现统计平均值, 而不是真实的二次或余弦振动频率; 因此, 与全原子力场相比, 珠子质量的意义和重要性不那么严格.
现在开始流程的试错部分. 写下每个势函数中涉及原子的相关段, 函数编号, 以及平衡值和力场数的初始猜测.
Martini通常使用1型键, 力常数通常处于10<sup>3</sup> kJ/mol•nm<sup>2</sup>范围内.
角度通常使用类型2, 因为它们在180°处不会变得不稳定. 力常数通常处于10<sup>2</sup> kJ/mol范围内.
最后, 二面角通常被设为类型1(力常数处于10<sup>0</sup> kJ/mol范围内), 或者, 当保持结构如环的平面性时, 设为类型2(力常数处于10<sup>2</sup> kJ/mol•rad<sup>2</sup>范围内).
这说明, 作为体系参数化的最高执行者, 你可以完全自由地选择使用哪些势函数(甚至可以使用非解析的列表势函数, 虽然它们有点偏离本教程的范围). 然而...
DIFFICULTY WARNING 困难警告
该映射涉及的键角可以达到180°. 在这些键上施加二面角势将导致严重的不稳定性. 我们建议, 为了及时和成功地完成教程, 跳过重现二面角分布. 如果你敢走这条路径采取以下建议:
这样, 我们就可以开始测试我们全新的粗粒化分子(在.itp文件中不再需要更多的指令).
创建.top文件, 其中使用#includes包含martini_v2.2.itp文件(其中定义了珠子之间的相互作用)以及刚刚创建的PEG的.itp文件(你可以使用全原子的topol.top作为模板). 指定体系中有多少分子, 就完成了.
第一步是生成一个足够稳定的粗粒化构象用来开始模拟. 将提供的em.mdp与刚刚创建的.top文件和先前映射的cg.gro一起使用:
grompp -f ../em.mdp -p topol.top -c cg.gro
你可能会收到一条警告, 告诉你原子名称不匹配. 这是可以忽略, 只要你明白为什么会出现这种差异(你明白, 对吧?). 使用-maxwarn 1标志重新运行grompp命令, 并使用以下命令最小化结构:
mdrun -v -rdd 1.4 -c em.gro
mdrun完成后, 会将最小化的坐标输出到em.gro文件. 注意选项-rdd 1.4, 它告诉GROMACS当进行并行化时, 要进一步搜索相邻单元格中的键合珠子. 在你的模拟中可能不是必需的, 而且使用这个选项会导致性能损失. 然而, 如果需要这个选项而你忽略了, 你会得到大量错误信息抱怨"missing interactions".
这时, 阅读em.mdp并查看Martini所需的选项是有益的. 在这个特殊情况下, 静电处理是不必要的, 因为我们的体系中没有电荷. 还要注意的是, Martini势函数的典型平滑性使得我们可以直接使用最陡下降最小化方法(.mdp文件中integrator=steep), 而不必担心体系被限制在离能量最小值太远的位置.
接下来, 准备MD运行:
grompp -f ../md.mdp -p topol.top -c em.gro
你不应该得到有关原子名称的进一步警告, 因为它们已经在em.gro中整理好了. 但是, 你可能被警告, 时间步长对于一些键合势函数产生的预期频率来说太大了. 如果这是你的第一次尝试, 请降低出问题的力常数. 如果在必须使用高的力常数来匹配键分布之后得到这些警告, 那么可以通过使用约束来替换它们. 如果减小了它们的时间常数, 你也可能会得到恒温器和恒压器的不是弱耦合的警告. 这些在Martini中通常是可以忽略的, 虽然取决于你能证明压力和温度行为是足够好的.
你现在可以(最后!)运行参数化PEG的MD模拟了!
mdrun -v -rdd 1.4
当模拟进行时, 你可以阅读.mdp文件, 并理解其控温和控压选项. Martini传统上与berendsen恒温器和恒压器耦合, 尽管也可以使用其他组合方案. 在大多数简单情况下, Martini和berendsen方案的稳健性允许我们忽略任何NVT预平衡步骤.
如果在这时上出现错误, 可能有多种原因, 而且GROMACS并不总是能完全退出, 并给出有用的信息. 最常见的情况是:
.mdp中设定的精度(参见lincs_order和lincs_iter选项), 约束网络不能正确地满足;当然, 还可能有许多其他原因造成不稳定. 减少时间步长通常会有帮助, 但这是不可取的(Martini典型时间步长的目标是20 fs). 有时使用小时间步长运行短时的NVT模拟会使体系变得足够稳定, 从而能够在更大时间步长下继续进行NPT模拟. 此外, 良好的诊断过程是创建一个输出每个模拟步的.mdp. 这将让你能够准确地识别出导致崩溃的事件.
当你得到一个稳定的运行, 继续...
在这一步, 你将简单地对粗粒化轨迹重新运行分析工具. 非常重要的是, 在分析之前, 你必须保证分子穿过PBC时保持完整:
trjconv -f traj.xtc -pbc mol -o trajpbc.xtc -b 1000
-b选项忽略作为预平衡的前1 ns轨迹. 现在可以使用calc_dists.sh脚本, 但务必保证其中的文件位置正确.
还要计算体系的密度. 除非你使用了特定的珠子质量, 否则g_energy将无法给出正确的密度值. 对输出的ener.edr文件简单运行g_energy来获取平均体积, 并使用已知的体系质量来计算密度.
最后, 使用g_polystat计算聚合物链的平均回转半径. 使用从这次运算中产生的.tpr文件, 你现在还可以计算全原子的回转半径, 如果你还没有这样做.
现在使用你最喜欢的绘图工具将得到的分布, 平均密度和回转半径与全原子的目标结果进行比较.
不太可能第一次尝试就完全正确地匹配所有分布和目标性质. 现在是时候创建一个take1目录, 并将新运行所需的文件放到里面. 复制PEG.itp并根据分布/性质差异对其进行调整. 为了防止较长的平衡时间, 一个好的做法是, 使用前一个take的输出构型作为新参数化测试运行的起始构型. 小心那些终止构象明显不稳定, 或经历不需要相变的运行.
留心, 当参数化溶剂或本教程的熔体时, 检查密度是否偏离目标值太大. 超过5-10%的差异很难通过单独调整键合势函数进行校正, 你可能需要重新思考所用的珠子类型.
重复上面的步骤, 直到你对得到结果满意. 如果是这样, 恭喜你, 你已经参数化了你的第一个Martini聚合物! 去喝杯马提尼酒庆祝一下吧.
在我们的方法中, 我们专注于重现聚合物的键合行为. 非键部分通过选择代表PEG化学本质, 并能得到正确密度的Martini结构单元来解决. 然而, Martini的理念要求更细致的方法, 对分子的分配性质与实验或模拟数据进行比较.
通常, 自由能与在水溶液和非极性溶剂之间的分配数据相匹配. 这源于Martini是用于生物分子模拟的力场. 然而, 应该强调的是, 这种参数化方法必须适应正在研究的问题. 例如, 如果模型的应用主要涉及与疏水性分子的相互作用, 那么目标中应该注重分配性质.
我们的PEG9分子的溶剂化自由能已经通过热力学积分(TI)方法在细粒度水平上确定了. 你可以点击此处获取该数据. 相同的存档文件中包含一个CG目录, 其中的H2O和Melt子目录, 可用于处理你的体系.
在每一目录中, 你将执行模拟以计算各自的溶剂化自由能. 这将通过去耦溶质(单个PEG9分子)和每种溶剂之间的非键相互作用来实现. 去耦将逐步完成, 经历10步, 这样就可以计算每次之间的自由能差. 你将需要优化好的PEG的.itp拓扑文件, 两个.top文件: 一个用于熔体系统, 另一个用于1个PEG和几个水.
你可以使用参数化结束时的.gro文件作为起点, 计算PEG9进入其自身熔体的溶剂化能. 然而, 我们需要告诉GROMACS我们希望将一个分子与所有其他分子去耦合.
GROMACS具有几种方式指定如何在耦合和去耦合状态之间切换. 这里我们通过将要去耦合分子的名称传递给.mdp中的couple_moltype选项来实现. 然而, 对于熔体, 这将意味着所有分子将同时被去耦合. 解决方法是复制并更改PEG.itp文件的名称, 然后更改其中的分子名称(例如PEG9X). 这就可以在.top文件中分开指定两种"不同"的分子:
[ molecule ]
PEG9X 1
PEG9 199
对于水系统, 你需要创建一个含有溶剂化的PEG9链的.gro文件. 一个简单的方法是使用与上述步骤相同的.gro文件, 但将.top更改为:
[molecule]
PEG9 1
W 1990
这将告诉GROMACS将第一个PEG后的任何原子都视为水珠子. 然后, 在将其用于TI之前, 需要平衡此系统一段时间(使用提供的eq.mdp文件).
为了在耦合和去耦合状态之间切换, 我们在.mdp文件中定义11个状态, 每个状态具有不同强度校正因子的范德华相互作用(更多的步骤需要关闭库伦相互作用, 但在我们的体系中不存在库伦相互作用). 强度校正因子由变量lambda定义, 其在0和1之间变化. lambda = 0和lambda = 1的含义由.mdp中的couple-lambda0和couple-lambda1来设定. 在我们的.mdp文件中, lambda = 0表示完全的范德华耦合(couple-lambda0=vdw), 而lambda = 1表示完全去耦合的分子(couple-lambda0=none).
11个不同状态中每个状态的lambda值由.mdp中的vdw-lambdas选项给出; init-lambda-state选项告诉GROMACS在特定的运行中实际使用10个lambda中的哪一个. 模拟将周期性地输出体系的势能(输出频率由nstdhdl选项控制). 我们将要使用的分析方法要求, 对于给定的状态, 相同的构象在所有其他状态下的能量也要输出. 这可以使用calc-lambda-neighbors = -1来设置(这也是为什么每个运行都需要知道有哪些其他状态).
你会在每个H2O和Melt子目录中找到一个TI.sh脚本. 此文件会自动生成要运行的10个体系. 仔细阅读并理解脚本如何根据每个解耦步骤修改.mdp文件(提示: 查看sedstate标签, sed命令使用它来创建不同步骤的文件). 还要注意它是如何将dhdl.xvg输出文件链接到根目录以便进行进一步分析的.
我们将使用MBAR积分和误差估计方法(方法的详细描述以及使用的分析脚本参见AlchemistryWiki). 我们提供了一个用于分析的python脚本, 但它需要pymbar安装包. 如果还没有安装, 你可以用:
sudo pip install pymbar==2.1.0-beta
进行安装(如果你没有工作站的sudo权限, 你可以通过传递--user选项将pymbar安装到你本地的主目录).
在完成所有运行后, 在H2O和Melt目录中, 使用提供的alchemical-gromacs.py脚本(来源于http://github.org/choderalab/pymbar-examples), 并给出输出文件名的前缀(-p选项), 温度(-t选项)和忽略多少ps作为平衡时间(-s选项; 1000 ps足够了):
python ../../alchemical-gromacs.py -p dhdl -t 300 -s 1000
输出中会给出使用不同方法的计算结果. 你应该使用来自MBAR的结果. 脚本的输出文件中还会给出各步骤之间的单个自由能变化值, 并识别出应该运行更多lambda点以降低估计误差的区域(但要注意, 因为需要计算所有步骤的能量, 如果你添加了更多的lambda点, 所有 步骤都必须重新运行).
在成功地参数化并模拟了你的新分子后, 你可能需要将其转换回精细结构(例如, 在使用粗粒化平衡体系后再进行细粒度模拟). 这个过程称为反向映射(或逆映射).
由于粗糙化过程中自由度数目会减小, 反向映射过程并不唯一: 一个粗粒化结构可以对应于多个全原子构象. 然而, 原子拓扑的信息使得我们可以输入更多的数据: 准备初始的全原子构象, 其中原子随机地置于粗粒化珠子附近. 然后就可以对体系进行受限于一些约束下的能量最小化和平衡. 拓扑中包含的键合信息会使得我们能够得到与初始粗粒化构象一致的细粒度构象. 在继续之前, 您可以在这里和这里以了解有关过程的更多信息.
要逆映射你的粗粒化PEG体系, 你需要使用backward工具. 点击这里下载并将其解压到新文件夹中. 现在将CG的.gro文件, 细粒度的.top文件及其引用的PEG9.itp一起复制到同一文件夹. 这些信息足以重建与GROMOS 54a7兼容的结构.
现在必须我们将PEG映射变为反向映射过程. 这通过创建一个.map文件完成, 其格式说明见这里, 但你也可以从Mapping目录复制一个已存在的文件(在你下载的教程目录的根目录中你也可以找到一个准备好的示例).
在.map文件中, 你需要将[ molecule ]命名为用于每个粗粒化PEG残基的名称. 如果你将残基命名为不同的名字(比方说, 为了区分末端), 最好编辑你的粗粒化.gro文件, 并将它们全部设置为相同的名称.
在[ martini ]指令下, 你可以输入构成每个残基的珠子的名称. 在我们的情况下, 每个残基由单个珠子组成. 同样, 这些珠子在.gro文件中应该都具有相同的名称; 否则的话, 编辑并修改文件.
[ mapping ]指令列出了此映射设置的力场. 它作为存在多重映射时的标签, 并且让脚本知道目标力场(粗粒化, 联合原子或全原子)的详细程度. 因为我们将反向映射到gromos54a7力场, 你可以设置为这个名字(目前的脚本识别martini, gromos, gromos43a2, gromos45a3, gromos53a6, gromos54a7, charmm, charmm27和charmm36).
最后, 在[ atoms ]指令下, 你要列出构成每个残基的原子编号和名称, 以及它们属于哪个粗粒化珠子. 格式为atom_number atom_name bead1 bead2 .... 检查全原子.itp文件中正确的原子名称. 此时, 你应确保.itp中的残留编号与映射一致. 你还应该检查每个残基没有重复的原子名称. 这是因为原子到珠子坐标的指定方法如下进行:
.gro文件中读取对应于残基n的珠子;.map文件中的相匹配, 并且划分到从.gro文件中读取的相应珠子上;最后一个规则意味着你可以忽略.map文件中特定的末端原子, 这可以简化列表.
在[ atoms ]指令之后, 你可以选择增加有关原子在珠子内相对位置的进一步信息. 在我们的情况下这没有必要. 如果原子拓扑可能导致最小化到错误的构象, 例如手性中心反转, 这将是需要的.
一旦完成后, .map文件必须放在Mapping目录中(实际上具有.map扩展名). 然后只需运行以下命令(指定正确的.gro和.top文件名):
./initram.sh -f cg.gro -p topol.top -to gromos54a7
这个shell脚本自动调用backward.py来生成起始的原子结构, 并运行一些适当的最小化和约束平衡步骤; initram.sh和backward.py都接受-h选项列出过程需要的所有选项.
一旦initram.sh完成, 你就准备好了原子体系! 可视化地叠加粗粒化和原子的.gro文件来判断转换的质量. 或者对生成的结构进行测试模拟, 模拟时使用合适的.mdp文件, 你可以在AA目录中找到它.
如果在最小化/平衡过程中出现错误并退出, 你可以尝试重新运行: 将原子分配到珠子空间是随机进行的, 运气不佳可能导致错误的反向映射.