对未知曲面进行插值, 在处理数据中经常用到. 我们这里所谓的曲面, 指的是以 $x, y, z$ 坐标给出的一些点. 这些点决定了一个单值曲面 $z=f(x,y)$, 但我们并不知道 $f(x,y)$ 的具体形式. 否则的话, 我们就可以进行拟合, 而无须插值了.
给出的格点数据可分为两类. 一类是规则数据, 也称均匀数据, 就是按一定步长对X-Y平面进行分格, 给出 $N_x \times N_y$ 个 $x,y, z$ 数据. 对这种数据, 插值相对容易, 样条函数法, 卷积法效果都不错. 我也写过一段代码进行这种规则数据的三次卷积插值. 如果给出的 $x, y,z$ 数据是随意的, 并不遵循某种规则, 这种无规则数据也称为非均匀数据. 非均匀数据的插值相对较困难, 不同插值的方法可以给出大不相同的曲面.
对非均匀曲面的插值, 常用的方法有样条函数法, 径向基函数法, Matlab的v4方法, 还有高斯过程法(Kriging为其中一种). 具体的理论还是很复杂的, 这里就不细究了, 只关注如何使用Matlab对曲面进行插值.
Matlab自带的曲面插值函数为griddata, 但这个函数效果不好, 所以有人开发了新函数gridfit, 很多人使用这个函数. 又有人在gridfit基础之上开发了RegularizeData3D, 效果更好, 这是目前最好的曲面插值函数, 建议优先使用.
除了使用这两个函数进行曲面插值之外, 也还有其他的一些方法. 如有人提到
先用tri = delaunay(x,y)对区域进行三角剖分, 让点自行连接成一个个三角形, 然后使用trisurf(tri,x,y,z)生成曲面, 再用shading interp插值拟合. 注意, 如果你的曲面在xy平面的投影不是矩形, 要用inpolygon把不在区域内的点删掉.
这种方法可行, 但稍嫌麻烦, 效果也未必好, 仅供参考.
对于Kriging方法, 效果也不错, 但比较复杂, 控制参数很多, 要知晓很多知识才能熟练使用, 不太适合用于简单的插值. 如果需要使用, 请参阅下面参考资料中的相关链接.
下面是使用griddata以及RegularizeData3D函数进行曲面插值并计算插值曲面曲率的示例代码, 供参考. 点击这里下载相关的文件.
<table class="highlighttable"><th colspan="2">matlab</th><tr><td><div class="linenodiv" style="background-color: #f0f0f0; padding-right: 10px"><pre style="line-height: 125%"> 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81</pre></div></td><td class="code"><div class="highlight" style="background: #f8f8f8"><pre style="line-height: 125%"><span style="color: #008800; font-style: italic">%% 根据离散点坐标(x,y,z), 插值生成空间曲面</span>
clc; clear; clear all;
<span style="color: #008800; font-style: italic">% 载入数据文件</span>
<span style="color: #008800; font-style: italic">% 数据文件每行三个数值分别为x, y, z坐标, 各数值之间以空格作为分隔符</span>
<span style="color: #008800; font-style: italic">% load xyz.dat</span>
<span style="color: #008800; font-style: italic">% 或使用下面的测试数据,8个离散点的xyz坐标</span>
xyz=[
<span style="color: #666666">1</span> <span style="color: #666666">0.5</span> <span style="color: #666666">0.5</span>
<span style="color: #666666">1</span> <span style="color: #666666">2</span> <span style="color: #666666">1</span>
<span style="color: #666666">1</span> <span style="color: #666666">3.5</span> <span style="color: #666666">0.5</span>
<span style="color: #666666">3</span> <span style="color: #666666">0.75</span> <span style="color: #666666">0.5</span>
<span style="color: #666666">3</span> <span style="color: #666666">1.5</span> <span style="color: #666666">1</span>
<span style="color: #666666">3</span> <span style="color: #666666">2.25</span> <span style="color: #666666">0.5</span>
<span style="color: #666666">3</span> <span style="color: #666666">3</span> <span style="color: #666666">1</span>
<span style="color: #666666">3</span> <span style="color: #666666">4</span> <span style="color: #666666">0.5</span>
];
<span style="color: #008800; font-style: italic">% 获取xyz数据xyz坐标</span>
x=xyz(:,<span style="color: #666666">1</span>); y=xyz(:,<span style="color: #666666">2</span>); z=xyz(:,<span style="color: #666666">3</span>);
<span style="color: #008800; font-style: italic">% 生成规则网格坐标X和Y</span>
dX=<span style="color: #666666">0.1</span>; dY=dX; <span style="color: #008800; font-style: italic">% X和Y方向步长均取0.1</span>
Xmin=min(x)<span style="color: #666666">-</span>dX; Ymin=min(y)<span style="color: #666666">-</span>dY; <span style="color: #008800; font-style: italic">% X和Y方向范围</span>
Xmax=max(x)<span style="color: #666666">+</span>dX; Ymax=max(y)<span style="color: #666666">+</span>dY;
<span style="color: #008800; font-style: italic">% 对网格进行插值生成相应的z坐标</span>
<span style="color: #008800; font-style: italic">% 注意: 不同插值方法得到的曲面不同</span>
<span style="color: #008800; font-style: italic">% 内置函数, 建议优先使用v4</span>
[X,Y]=<span style="color: #AA22FF">meshgrid</span>(Xmin:dX:Xmax, Ymin:dY:Ymax);
Zv4=griddata(x,y,z, X,Y,<span style="color: #BB4444">'</span>v4<span style="color: #666666">'</span>);
<span style="color: #008800; font-style: italic">% 外部函数, 优先使用bicubic方法, Bilinear得到的结果可能不正确</span>
X=Xmin:dX:Xmax;
Y=Ymin:dY:Ymax;
Smoothness=<span style="color: #666666">0.0001</span>; <span style="color: #008800; font-style: italic">% 控制曲面光滑程度, 越小越接近数据点</span>
Zreg=RegularizeData3D(x,y,z, X,Y, <span style="color: #BB4444">'</span>interp<span style="color: #666666">'</span>, <span style="color: #BB4444">'</span>bicubic<span style="color: #666666">'</span>, <span style="color: #BB4444">'</span>smoothness<span style="color: #666666">'</span>, Smoothness);
<span style="color: #008800; font-style: italic">% 绘制离散点及插值曲面</span>
figure(<span style="color: #666666">1</span>)
plot3(x,y,z, <span style="color: #BB4444">'</span>r.<span style="color: #666666">'</span>,<span style="color: #BB4444">'</span>MarkerSize<span style="color: #666666">'</span>,<span style="color: #666666">30</span>)
hold on; grid on
mesh(X,Y,Zv4, <span style="color: #BB4444">'</span>facealpha<span style="color: #666666">'</span>,<span style="color: #666666">0</span>)
surf(X,Y,Zreg, <span style="color: #BB4444">'</span>facealpha<span style="color: #666666">'</span>,.<span style="color: #666666">75</span>, <span style="color: #BB4444">'</span>FaceColor<span style="color: #666666">'</span>,<span style="color: #BB4444">'</span>interp<span style="color: #666666">'</span>, <span style="color: #BB4444">'</span>EdgeColor<span style="color: #666666">'</span>,<span style="color: #BB4444">'</span>none<span style="color: #666666">'</span>)
title({<span style="color: #BB4444">'</span><span style="color: #666666">\</span>fontname{微软雅黑}不同插值方法得到的曲面<span style="color: #BB4444">'</span>; <span style="color: #008800; font-style: italic">...</span>
<span style="color: #BB4444">'</span>线框: griddata<span style="color: #666666">-</span>v4 表面: RegularizeData3D<span style="color: #666666">-</span>bicubic<span style="color: #666666">'</span>})
<span style="color: #008800; font-style: italic">%% 根据插值曲面计算曲面曲率</span>
figure(<span style="color: #666666">2</span>)
[X,Y]=<span style="color: #AA22FF">meshgrid</span>(Xmin:dX:Xmax, Ymin:dY:Ymax);
[K,H,P1,P2] = surfature(X,Y,Zreg);
surf(X,Y,Zreg,H,<span style="color: #BB4444">'</span>facecolor<span style="color: #666666">'</span>,<span style="color: #BB4444">'</span>interp<span style="color: #666666">'</span>);
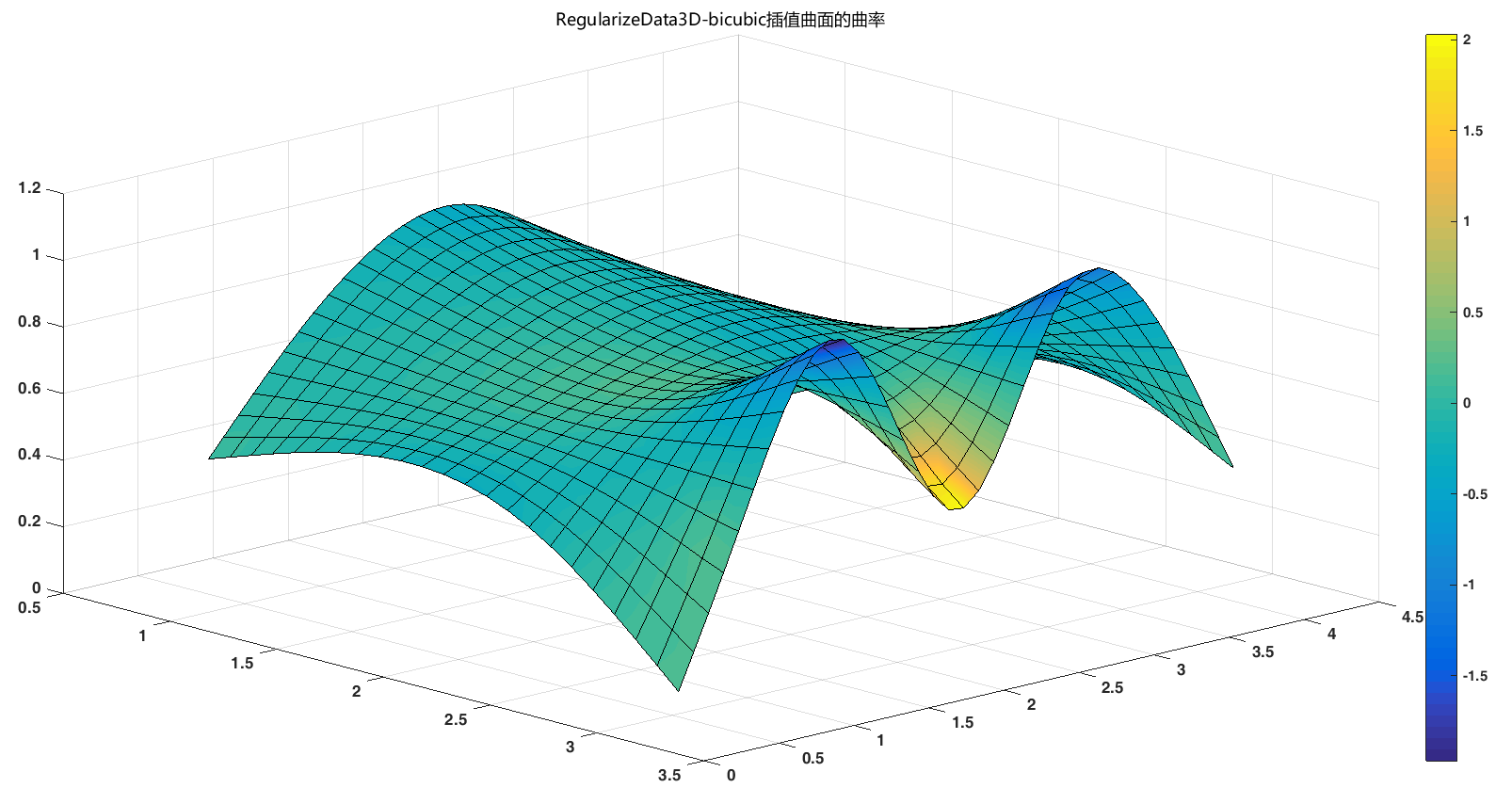
title <span style="color: #BB4444">'</span><span style="color: #666666">\</span>fontname{微软雅黑}RegularizeData3D<span style="color: #666666">-</span>bicubic插值曲面的曲率<span style="color: #BB4444">'</span>
<span style="color: #008800; font-style: italic">%% 径向基Multiquadric插值方法</span>
<span style="color: #008800; font-style: italic">% 结果与RegularizeData3D-bicubic相差不大, 可用于研究具体算法的实现</span>
<span style="color: #008800; font-style: italic">%{</span>
<span style="color: #008800; font-style: italic">[xj,xi]=meshgrid(x);</span>
<span style="color: #008800; font-style: italic">[yj,yi]=meshgrid(y);</span>
<span style="color: #008800; font-style: italic">dij2=(xi-xj).^2+(yi-yj).^2;</span>
<span style="color: #008800; font-style: italic">idls=logical(tril(ones(length(x)),-1));</span>
<span style="color: #008800; font-style: italic">idx=dij2(idls)>0;</span>
<span style="color: #008800; font-style: italic">if all(~idx)</span>
<span style="color: #008800; font-style: italic"> delta=1/618;</span>
<span style="color: #008800; font-style: italic">else</span>
<span style="color: #008800; font-style: italic"> delta=1/max(sqrt(dij2(idx)));</span>
<span style="color: #008800; font-style: italic">end</span>
<span style="color: #008800; font-style: italic">Q=sqrt(dij2+delta^2);</span>
<span style="color: #008800; font-style: italic">alpha=Q\z;</span>
<span style="color: #008800; font-style: italic">[X,Y]=meshgrid(Xmin:dX:Xmax, Ymin:dY:Ymax);</span>
<span style="color: #008800; font-style: italic">[Xj,Xi]=meshgrid(x,X);</span>
<span style="color: #008800; font-style: italic">[Yj,Yi]=meshgrid(y,Y);</span>
<span style="color: #008800; font-style: italic">Z=sqrt((Xi-Xj).^2+(Yi-Yj).^2+delta^2)*alpha;</span>
<span style="color: #008800; font-style: italic">hold on</span>
<span style="color: #008800; font-style: italic">surf(X,Y,reshape(Z,size(X)));</span>
<span style="color: #008800; font-style: italic">%}</span>
</pre></div>
</td></tr></table>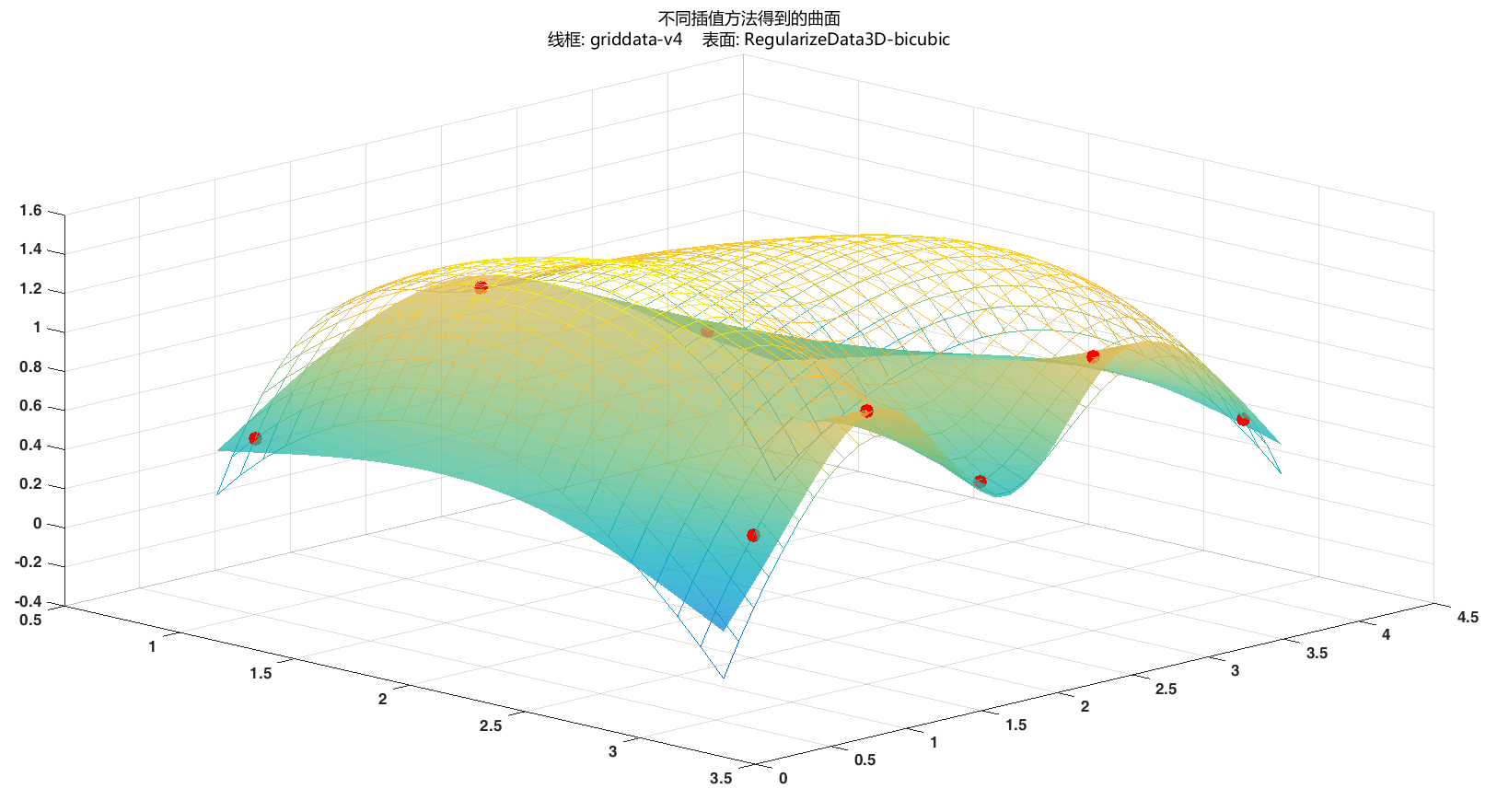
参考资料


