我的gmx_mmpbsa脚本发布时间也不短了, 有不少人用过, 也有些人在文章中引用. 但凡一件事物, 用的人多了, 总会暴露出一些问题与缺陷, 于代码而言, 尤其如此. 查看总结网上涉及gmx_mmpbsa的留言与问题后, 我觉得有必要更新一下这个脚本, 其中最主要的一点就是, 试着解决所得结合能数值不合理的问题.
在计算两个组分, 如蛋白和配体的结合能时, 如果其中一个或两个组分带有净电荷, 气相MM部分的静电相互作用MM(COU)往往会很大, 从而导致总的结合能绝对数值过大或为正值. 这并不是什么计算错误, 而是由MMPBSA这个方法的近似导致的. 虽然计算MM(COU)时可以引入溶质的介电常数对此进行校正, 但具体使用什么数值, 文献上并没有定论. 一些讨论可以参考文献[^1].
最近有篇论文[^2]使用gmx_mmpbsa研究了新冠病毒与ACE2, 两种抗体的结合能. 由于涉及到的蛋白都带有很大的净电荷, 直接使用原始MMPBSA方法自然会得到非常大的结合能, 远远大于实验值, 明显与实验结果不符, 而且连相对强弱顺序也与实验结果不一致. 为此, 文章的作者建议使用德拜-休克尔屏蔽方法计算MM(COU): 计算MM(COU)时使用考虑离子强度, 使用德拜特征长度对静电作用进行指数衰减. 这样处理后, 所得MM(COU)贡献就变小了, 再加上考虑熵的贡献, 最终所得的结合能总算与实验值比较一致了, 相对强弱顺序也能对得上了.
我不是专门研究自由能计算的, 所以也不太关注这些, 但鉴于他们是基于自行修改的gmx_mmpbsa脚本进行计算的, 所以我觉得还是将他们的方法集成到我的脚本中去, 弄成类似官方支持吧, 这样如果有人需要使用这种方法, 能更方便一些.
代码
见https://jerkwin.github.io/gmxtools/.
几点说明:
- 这种屏蔽方法实现起来并不复杂, 但需要指出论文[^2]中所给德拜长度公式存在笔误, 根号应该扩展到整个表达式. 此外, 公式中的相对介电常数应该用水的值.
- 脚本将PB计算的默认方法由线性lpbe方法改为非线性npbe方法. 根据一些资料的说法, 对于净电荷很大的体系, lpbe方法误差过大. 根据维基, 改为npbe后, 所得PB相互作用能会变小.
- 再次强调, 网格参数
df对PB结果的影响非常显著, 默认值0.5可能并未达到收敛的结果. 如果要仔细对待结果, 那么请牢记这一点.
简单测试
1EBZ: 屏蔽效应并不显著
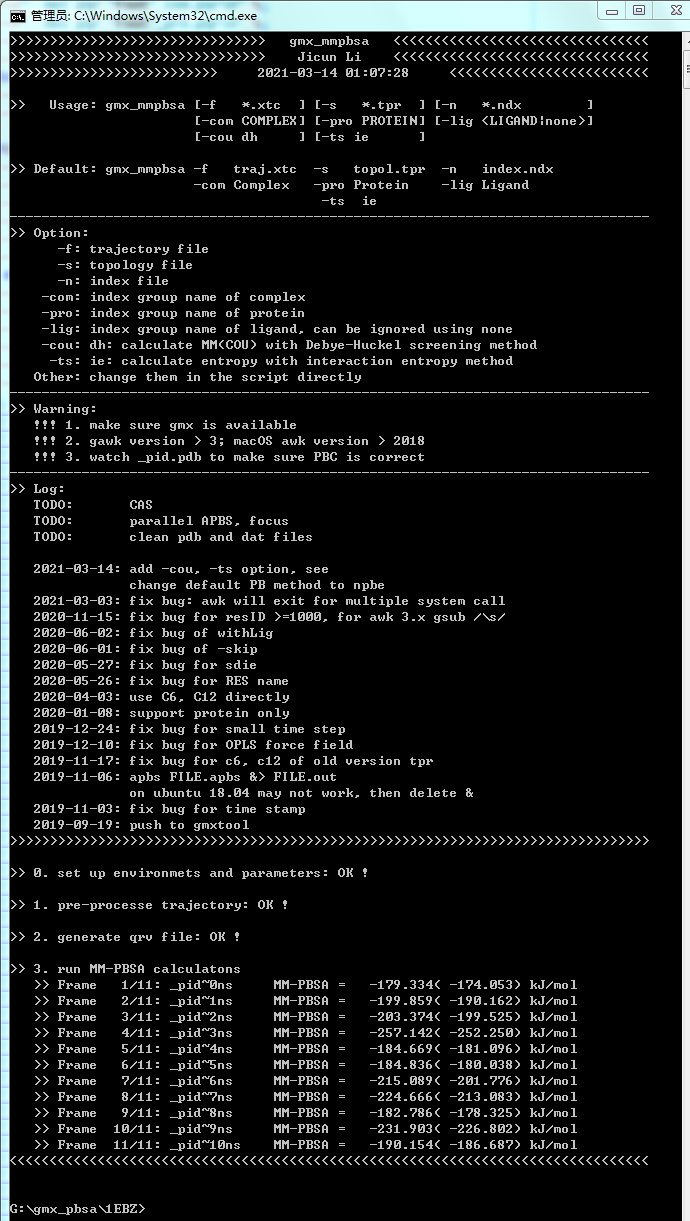
<table id='tab-0'><caption>1EBZ轨迹MMPBSA计算结果 <input type='button' id='tab-0_tog' value='折叠表格' onclick="togtab('tab-0', this.value)"></caption><tr>
<th rowspan="1" colspan="1" style="text-align:center;">#Frame</th>
<th rowspan="1" colspan="1" style="text-align:center;">Binding( with DH )</th>
<th rowspan="1" colspan="1" style="text-align:center;">MM ( with DH )</th>
<th rowspan="1" colspan="1" style="text-align:center;">PB</th>
<th rowspan="1" colspan="1" style="text-align:center;">SA</th>
<th rowspan="1" colspan="1" style="text-align:center;">COU ( with DH )</th>
<th rowspan="1" colspan="1" style="text-align:center;">VDW</th>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">0ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-179.334( -174.053)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-468.203( -462.922)</td>
<td rowspan="1" colspan="1" style="text-align:center;">323.523</td>
<td rowspan="1" colspan="1" style="text-align:center;">-34.654</td>
<td rowspan="1" colspan="1" style="text-align:center;">-147.070( -141.788)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-321.134</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">1ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-199.859( -190.162)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-488.041( -478.344)</td>
<td rowspan="1" colspan="1" style="text-align:center;">322.631</td>
<td rowspan="1" colspan="1" style="text-align:center;">-34.449</td>
<td rowspan="1" colspan="1" style="text-align:center;">-176.307( -166.610)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-311.734</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">2ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-203.374( -199.525)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-484.874( -481.025)</td>
<td rowspan="1" colspan="1" style="text-align:center;">316.239</td>
<td rowspan="1" colspan="1" style="text-align:center;">-34.740</td>
<td rowspan="1" colspan="1" style="text-align:center;">-146.223( -142.374)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-338.651</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">3ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-257.142( -252.250)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-555.574( -550.682)</td>
<td rowspan="1" colspan="1" style="text-align:center;">332.083</td>
<td rowspan="1" colspan="1" style="text-align:center;">-33.651</td>
<td rowspan="1" colspan="1" style="text-align:center;">-179.019( -174.127)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-376.555</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">4ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-184.669( -181.096)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-474.791( -471.219)</td>
<td rowspan="1" colspan="1" style="text-align:center;">323.676</td>
<td rowspan="1" colspan="1" style="text-align:center;">-33.553</td>
<td rowspan="1" colspan="1" style="text-align:center;">-144.987( -141.414)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-329.804</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">5ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-184.836( -180.038)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-480.970( -476.172)</td>
<td rowspan="1" colspan="1" style="text-align:center;">330.706</td>
<td rowspan="1" colspan="1" style="text-align:center;">-34.573</td>
<td rowspan="1" colspan="1" style="text-align:center;">-162.984( -158.186)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-317.986</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">6ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-215.089( -201.776)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-513.379( -500.066)</td>
<td rowspan="1" colspan="1" style="text-align:center;">331.582</td>
<td rowspan="1" colspan="1" style="text-align:center;">-33.292</td>
<td rowspan="1" colspan="1" style="text-align:center;">-181.463( -168.149)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-331.917</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">7ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-224.666( -213.083)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-505.049( -493.466)</td>
<td rowspan="1" colspan="1" style="text-align:center;">314.445</td>
<td rowspan="1" colspan="1" style="text-align:center;">-34.062</td>
<td rowspan="1" colspan="1" style="text-align:center;">-170.463( -158.879)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-334.587</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">8ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-182.786( -178.325)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-453.628( -449.167)</td>
<td rowspan="1" colspan="1" style="text-align:center;">304.229</td>
<td rowspan="1" colspan="1" style="text-align:center;">-33.387</td>
<td rowspan="1" colspan="1" style="text-align:center;">-134.991( -130.530)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-318.636</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">9ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-231.903( -226.802)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-513.090( -507.988)</td>
<td rowspan="1" colspan="1" style="text-align:center;">315.202</td>
<td rowspan="1" colspan="1" style="text-align:center;">-34.015</td>
<td rowspan="1" colspan="1" style="text-align:center;">-156.808( -151.707)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-356.282</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">10ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-190.154( -186.687)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-467.055( -463.589)</td>
<td rowspan="1" colspan="1" style="text-align:center;">310.690</td>
<td rowspan="1" colspan="1" style="text-align:center;">-33.788</td>
<td rowspan="1" colspan="1" style="text-align:center;">-140.663( -137.196)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-326.393</td>
</tr>
<tr>
<td rowspan="1" colspan="8" style="text-align:center;"></td>
</tr>
<tr>
<th rowspan="1" colspan="1" style="text-align:center;">mean</th>
<td rowspan="1" colspan="1" style="text-align:center;">-204.892( -198.527)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-491.332( -484.967)</td>
<td rowspan="1" colspan="1" style="text-align:center;">320.455</td>
<td rowspan="1" colspan="1" style="text-align:center;">-34.015</td>
<td rowspan="1" colspan="1" style="text-align:center;">-158.271( -151.906)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-333.062</td>
</tr>
<tr>
<th rowspan="1" colspan="1" style="text-align:center;">-TdS</th>
<td rowspan="1" colspan="1" style="text-align:center;">31.779( 29.874)</td>
<td rowspan="1" colspan="6" style="text-align:center;"></td>
</tr>
<tr>
<th rowspan="1" colspan="1" style="text-align:center;">dG</th>
<td rowspan="1" colspan="6" style="text-align:left;">-173.113( -168.653) kJ/mol = -41.375( -40.309) kcal/mol</td>
</tr>
</table>某蛋白-蛋白: 屏蔽效应显著
<table id='tab-1'><caption>蛋白-蛋白MMPBSA计算结果 <input type='button' id='tab-1_tog' value='折叠表格' onclick="togtab('tab-1', this.value)"></caption><tr>
<th rowspan="1" colspan="1" style="text-align:center;">#Frame</th>
<th rowspan="1" colspan="1" style="text-align:center;">Binding( with DH )</th>
<th rowspan="1" colspan="1" style="text-align:center;">MM ( with DH )</th>
<th rowspan="1" colspan="1" style="text-align:center;">PB</th>
<th rowspan="1" colspan="1" style="text-align:center;">SA</th>
<th rowspan="1" colspan="1" style="text-align:center;">COU ( with DH )</th>
<th rowspan="1" colspan="1" style="text-align:center;">VDW</th>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">20ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1325.265(-180.626)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1815.333( -670.694)</td>
<td rowspan="1" colspan="1" style="text-align:center;">524.813</td>
<td rowspan="1" colspan="1" style="text-align:center;">-34.745</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1611.968( -467.330)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-203.365</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">21ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1215.585(-109.710)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1900.597( -794.722)</td>
<td rowspan="1" colspan="1" style="text-align:center;">723.437</td>
<td rowspan="1" colspan="1" style="text-align:center;">-38.425</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1646.821( -540.946)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-253.776</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">22ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1452.256(-224.669)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-2026.828( -799.240)</td>
<td rowspan="1" colspan="1" style="text-align:center;">616.961</td>
<td rowspan="1" colspan="1" style="text-align:center;">-42.389</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1740.134( -512.547)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-286.694</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">23ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1547.032(-287.347)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-2095.682( -835.997)</td>
<td rowspan="1" colspan="1" style="text-align:center;">586.848</td>
<td rowspan="1" colspan="1" style="text-align:center;">-38.199</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1805.780( -546.095)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-289.901</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">24ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1305.430(-188.950)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1801.379( -684.899)</td>
<td rowspan="1" colspan="1" style="text-align:center;">535.587</td>
<td rowspan="1" colspan="1" style="text-align:center;">-39.638</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1535.285( -418.806)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-266.093</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">25ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1407.047(-229.259)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1940.299( -762.510)</td>
<td rowspan="1" colspan="1" style="text-align:center;">572.962</td>
<td rowspan="1" colspan="1" style="text-align:center;">-39.710</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1670.085( -492.296)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-270.214</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">26ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1410.308(-231.828)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1892.770( -714.290)</td>
<td rowspan="1" colspan="1" style="text-align:center;">525.772</td>
<td rowspan="1" colspan="1" style="text-align:center;">-43.310</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1586.906( -408.426)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-305.864</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">27ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1420.565(-214.647)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-2089.784( -883.866)</td>
<td rowspan="1" colspan="1" style="text-align:center;">715.753</td>
<td rowspan="1" colspan="1" style="text-align:center;">-46.534</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1730.488( -524.570)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-359.296</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">28ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1429.163(-206.088)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1972.306( -749.231)</td>
<td rowspan="1" colspan="1" style="text-align:center;">587.422</td>
<td rowspan="1" colspan="1" style="text-align:center;">-44.279</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1679.958( -456.883)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-292.348</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">29ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1522.787(-265.283)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-2001.972( -744.468)</td>
<td rowspan="1" colspan="1" style="text-align:center;">520.315</td>
<td rowspan="1" colspan="1" style="text-align:center;">-41.130</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1724.539( -467.035)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-277.433</td>
</tr>
<tr>
<td rowspan="1" colspan="1" style="text-align:center;">30ns</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1464.768(-260.994)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1915.157( -711.384)</td>
<td rowspan="1" colspan="1" style="text-align:center;">494.979</td>
<td rowspan="1" colspan="1" style="text-align:center;">-44.590</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1607.751( -403.977)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-307.407</td>
</tr>
<tr>
<td rowspan="1" colspan="8" style="text-align:center;"></td>
</tr>
<tr>
<th rowspan="1" colspan="1" style="text-align:left;">mean</th>
<td rowspan="1" colspan="1" style="text-align:center;">-1409.110(-218.127)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1950.191( -759.209)</td>
<td rowspan="1" colspan="1" style="text-align:center;">582.259</td>
<td rowspan="1" colspan="1" style="text-align:center;">-41.177</td>
<td rowspan="1" colspan="1" style="text-align:center;">-1667.247( -476.265)</td>
<td rowspan="1" colspan="1" style="text-align:center;">-282.945</td>
</tr>
<tr>
<th rowspan="1" colspan="1" style="text-align:left;">-TdS</th>
<td rowspan="1" colspan="1" style="text-align:center;">142.877( 82.579)</td>
<td rowspan="1" colspan="6" style="text-align:center;"></td>
</tr>
<tr>
<th rowspan="1" colspan="1" style="text-align:center;">dG</th>
<td rowspan="1" colspan="6" style="text-align:left;">-1266.232(-135.548) kJ/mol = -302.637( -32.397) kcal/mol</td>
</tr>
</table>几点思考与想法
- 结合能的计算是一个系统流程, 需要全局考虑, 结合能每项贡献具体计算方法的不同都可能导致总结合能发生变化. 所以在对比评估不同计算流程时, 要考虑到这一点, 不要将不同计算流程的部分贡献拿来组合. 这么做可能会凑出看起来更好的结果, 但也可能只是误差抵消导致的假象. 当然了, 说成杂凑有点低陋, 说成杂化/杂合hybrid就高深多了, 各式论文中屡见不鲜.
- 屏蔽方法对某个特定体系能给出更好结果只是给出了一点线索, 要成为通用的方法可能还不够. 接下来需要对尽可能多的不同体系进行考察, 综合评定其效果. 浙大的侯廷军搜集整理了一个结合能数据库PDBbind, 并在论文[^3]中用于对比评判各种MMGBSA/MMPBSA流程. 同样, 我们可以用这个数据库来测评下屏蔽方法, 如果总体结果确是好于原始的MMPBSA方法, 也算是篇不错的论文. 有了这样的测评结果之后, 可以让人在使用这种方法时更有信心, 当然也可以吸引更多人来使用这种方法.
- 考虑屏蔽效应时, 离子浓度用的是所加盐的浓度(一般为0.15M). 如果模拟过程中没有加盐, 只添加了抗衡离子, 这种情况下还要考虑屏蔽效应么? 此外, 对每一帧NPT轨迹, 严格来说盐浓度也并非固定不变, 我觉得根据每帧轨迹的体积和总离子数目来计算屏蔽长度更说得通.
- 计算MM(COU)时也使用PB方法, 只不过改用不同的介电常数/原子半径, 是否可行? 不知道PB计算时原子半径是否可以设置为零.
- 论文[^4]中提出了一种电荷校正方法, 或许可以看看, 有什么启示.
参考文献
- Samuel Genheden, Ulf Ryde; The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities; Expert Opinion on Drug Discovery 10(5):449-461, 2015; 10.1517/17460441.2015.1032936
- Hong-ming Ding, Yue-wen Yin, Song-di Ni, Yan-jing Sheng, Yu-qiang Ma; Accurate Evaluation on the Interactions of SARS-CoV-2 with Its Receptor ACE2 and Antibodies CR3022/CB6*; Chinese Phys. Lett. 38(1):018701, 2021; 10.1088/0256-307X/38/1/018701
- Huiyong Sun, Youyong Li, Sheng Tian, Lei Xu, Tingjun Hou; Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set; Phys. Chem. Chem. Phys. 16(31):16719-16729, 2014; 10.1039/c4cp01388c
- Martin A. Olsson, Alfonso T. García-sosa, Ulf Ryde; Binding affinities of the farnesoid X receptor in the D3R Grand Challen; J Comput Aided Mol Des 32(1):211-224, 2017; 10.1007/s10822-017-0056-z

