title: "半监督学习简要" categories:
参考
书比较老, 介绍了 SVM 时代一些分类问题机器学习算法的半监督版本. 特色是强调半监督学习有效需要的假设, 以及不符合假设的人造数据样例的可视化展示. 本文只涉及通用的算法.
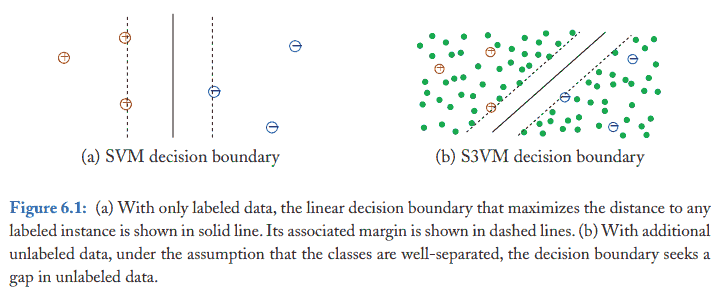
<!-- more -->假设依模型而定, 一般而言要假定同类数据聚集在一起, 或者对输入小扰动后输出也只会小扰动 (光滑). 下面是 SVM 的例子.
下面的图左上角和右下角分为两类标签, 但是数据聚集为左下角和右上角两块, 半监督学习由于不知道真实标签, 无法处理.
用有标签数据训练模型, 用训练好的模型预测无标签数据, 把部分无标签数据加入训练集 (预测标签视为真实标签). 重复上述过程. 比如可以选择模型认为把握很大的数据加入训练集.
假设: 模型预测准确, 至少对于它自己把握大的预测要准确.
首先数据特征分为不相交的两部分, 同时训练两个分类器, 用这两个模型分别预测无标签数据, 把模型最自信的一些无标签数据加入另一个分类器的训练集中 (同时). 重复上述过程.
假设:
书上的例子是命名实体分类, 把一个 sample 的特征分为两部分: 命名实体本身 $x^{(1)}$, 和它的上下文 $x^{(2)}$. 比如 samples 有
headquartered in (Washington State)
(Mr. Washington), the vice president
headquartered in (Kazakhstan)
flew to (Kazakhstan)
| $x^{(1)}$ | $x^{(2)}$ | $y$ |
|---|---|---|
| Washington State | headquartered in | Location |
| Mr. Washington | vice president | Person |
| Kazakhstan | headquartered in | ? |
| Kazakhstan | flew to | ? |
根据上下文 headquartered in 学习到它意味着地名后, 可以推测出拥有同样上下文的 Kazakhstan 是地名, 然后继续迭代又能学到 flew to 意为着地名等.
条件独立意味着
$$ \begin{align} \mathbb P(x^{(1)} \mid y, x^{(2)}) &= \mathbb P(x^{(1)} \mid y),\ \mathbb P(x^{(2)} \mid y, x^{(1)}) &= \mathbb P(x^{(2)} \mid y). \end{align} $$
对应例子就是, 知道是一个实体是地名后, 那么它是哪个地名, 不影响它的上下文特征的分布, 反之亦然. 但比如知道上下文特征是 "首都是" 之后, 地名只能是首都, 而不能是别的地名, 这就不符合条件独立性. 实际上除了这个假设难以满足, 把特征分为两部分本身就是很难操作的事情.
除了上面的两种 wrapper 方法 (具体的分类器不限), 半监督学习一般通过改造损失函数加入无标签数据, 而无标签数据的项又可以视为正则项...