title: "知识蒸馏简要" categories:
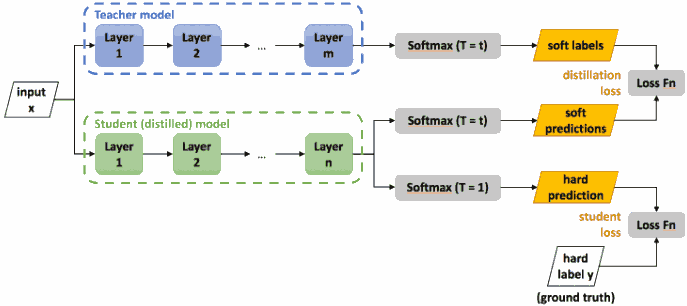
模型压缩, 用小模型向大模型学习. 神经网络最后一层通常将 logits $z_i$ 经过 softmax 函数转化为类别概率预测 $q_i$ 输出,
$$ q_i = \frac{\exp(z_i/T)}{\sum_j \exp(z_j/T)}, $$
其中 $T=1$. 这种概率预测称为 soft target/label (相对于 hard target, 即直接预测一个类别, 而不给与概率).
<!-- more -->以 MNIST 手写数字识别为例.
For example, one version of a 2 may be given a probability of $10^{−6}$ of being a 3 and $10^{−9}$ of being a 7 whereas for another version it may be the other way around. This is valuable information that defines a rich similarity structure over the data (i. e. it says which 2's look like 3's and which look like 7's) but it has very little influence on the cross-entropy cost function during the transfer stage because the probabilities are so close to zero.
在知识蒸馏中, 小模型 student model 要模仿大模型 teacher model 的概率预测. 然而在很多时候, 正确类别的预测概率非常大, 于是引入了上面式子中的 $T$ (称为温度参数). 参数 $T$ 越大, 则预测分布越接近均匀分布, 从而拔高了那些原先很小的概率预测, 使得整个分布更加平滑, 让模型学到这些 dark knowledge.
Hinton 发现用数据的 true labels 和教师模型的 soft-labels 同时训练学生模型会更好. 把两种 loss 加权如下.
$$ L = \alpha H(y, \sigma(z_s; T=1)) + \beta H(\sigma(z_t; T=\tau), \sigma(z_s; T=\tau)), $$
其中 $H$ 是交叉熵函数, $y$ 是真实标签, $\sigma$ 是带温度参数 $T$ 的 softmax 函数, $z_s$, $z_t$ 分别是学生模型和教师模型的 logits, $\alpha$ 和 $\beta$ 是权重.
训练完成后在预测阶段取 $T=1$.