title: "Bayes 优化简介" categories:
首先强烈推荐
写得非常清楚. 本文只简单介绍最基本的内容.
考虑优化问题
$$ \max_{x\in A} f(x), $$
Bayesian optimization is designed for black-box derivative-free global optimization. 黑箱意思是不知道函数 $f$ 的形式和性质 (凸性等), 只能通过输入 $x$ 得到输出 $f(x)$, 另外也不知道导数信息, 目标是求解全局最优.
<!-- more -->Bayes 优化由两部分组成: 目标函数上的 Bayes 模型, 以及用来决定下一步输入哪个值的 acquisition function. 场景是每次输入 $x$ 得到输出 $f(x)$ 有一定成本 (比如时间成本), 希望试最少的次数得到最大值.
GP regression is a Bayesian statistical approach for modeling functions. 现在有 $k$ 个点上的函数值 $f(x_{1:k}) := (f(x_1), \dots, f(x_k))$, 假设它是服从某个先验分布的随机向量的一个具体观测值. GP 把这个先验分布取为多元正态分布
$$ f(x_{1:k}) \sim \operatorname{Normal} (\mu0(x{1:k}), \Sigma0(x{1:k}, x_{1:k})), $$
其中 $\mu_0$ 和 $\Sigma0$ 自定义 (这里会引入新的超参数, 略). 对于新的点 $x$, 考虑后验分布 (条件分布) $f(x) \mid f(x{1:k})$, 它也是多元正态分布.
The most commonly used acquisition function is expected improvement. (此外还有 knowledge gradient, entropy search and predictive entropy search 等.) 要决定下一个点 $x$ 试哪里收益高, EI 根据历史观测, 取期望增益 (相比历史观测最大值) 最高的点, 即
$$ \operatorname{EI}_k(x) = \mathbb Ek \max(0, f(x) - \max{j\le k} f(x_j)), $$
其中 $\mathbb Ek$ 对应的分布为观测 $k$ 个点的后验分布. 然后下一个点 $x{k+1}$ 取为使这个期望最大的点
$$ x_{k+1} = \operatorname{argmax} \operatorname{EI}_k(x). $$
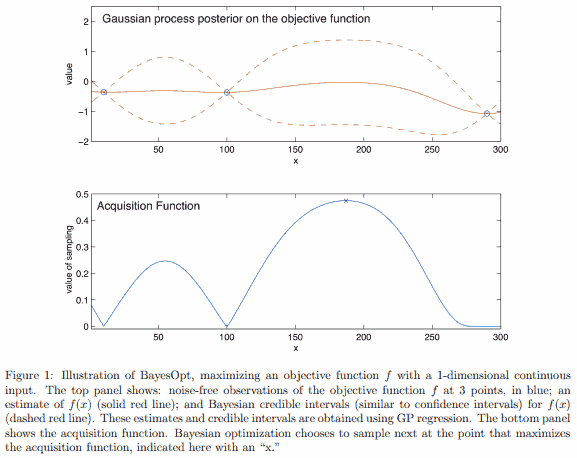
总得来说贝叶斯优化把原先的寻找超参数问题转换为在 surrogate model (GP) 上调超参, 求解 acquisition function 最大值的问题.