title: "Deep Learning for Time Series Probabilistic Forecasting" categories:
主要介绍 DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks, 其他方法暂时略讲. 附带讲一些我知道的统计学领域的方法. 例子依然主要以销量预测为例.
<!-- more -->尽量和原论文记号保持一致. 假设我们有 $N$ 条时间序列, $T$ 个时间点. 第 $i$ 条时间序列在时间 $t$ 的值记为 $z{i, t}$, 特征记为 $x{i,t}$ (向量). 为了符号简便, 去掉下标 $i$, 简记为 $z_t$, $x_t$. 记
$$ z_{t_1:t2} := (z{t1}, z{t1+1},\dots, z{t_2}) $$
为时间段 $[t_1, t2]$ 的序列. 类似地定义 $x{t_1:t_2}$, 并假设特征在所有时间点 (包括未来) 都是已知的. 假设历史序列时间段为 $[1, t_0-1]$, 未来为 $[t_0, T]$, 我们要建模条件似然
$$ P(z_{t0:T} | z{1:t0-1}, x{1:T}). $$
假设模型的条件似然为
$$ Q\Theta(z{ t0:T} | z{1:t0-1}, x{1:T}) = \prod_{t=t0}^T Q\Theta(z{t} | z{1:t0-1}, x{1:T}) = \prod_{t=t0}^T \ell(z{t}|\theta(h_{t}, \Theta)), $$
其中 (省略 $h$ 下标 $i$)
$$ ht = f(h{t-1}, z_{t-1}, x_t, \Theta), $$
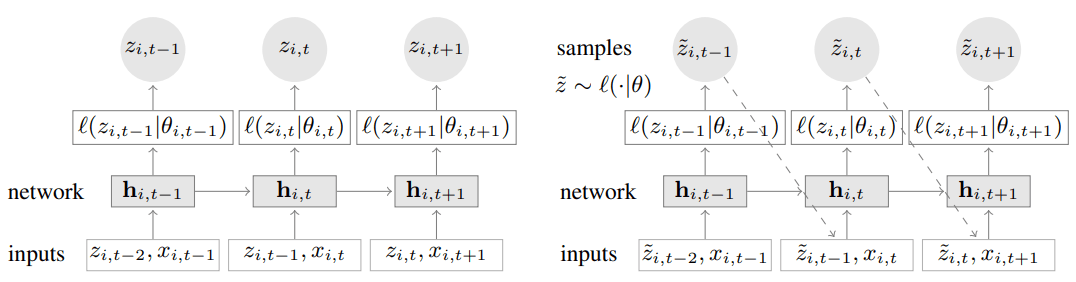
而 $f$ 表示多层 LSTM, 似然 $\ell$ 是根据指定的参数分布来取的 (如 Gauss, negative binomial).
生成预测样本的方法是迭代式 (很常见的做法): 根据选定的参数分布 sample 出一个值, 之后将这个值当成真实值继续 sample 下一个时间点的样本. 重复若干次, 再根据多条模拟样本估计感兴趣的分位数.
Gauss 和 negative binomial 分布可以用一阶矩和二阶矩完全刻画, 神经网络干的事情就是学习这俩参数. 目标是极大化 log 似然
$$ \sum{i=1}^N\sum{t=t0}^T \log \ell(z{i, t}|\theta(h_{i,t})). $$
特征: 价格, 促销, 'age' (the distance to the first observation in that time series), day-of-the-week, category embedding 等.
类似 cross-validation, 用一个 window 去截时间序列.
模型结构很简单, 就是常见的 RNN 变种. AR (autoregressive) 就在于上一个时间点的真值会被用来预测当前时间点的值.
总得来说就是假设时间序列的条件分布服从某个参数分布, 而这个参数是用神经网络学来的, 目标是最大化条件似然. 整个结构实际上就是统计学中 state space model 的结构, 唯一区别在于 $f$ 被换成了神经网络. 实际上也有直接标题为深度学习 ssm 的文章 Deep State Space Models for Time Series Forecasting, 但我还没读.
说回统计学, 在 Some Evaluations for Time Series Forecasting 里提到过销量属于计数时间序列, 关于计数时间序列的状态空间模型, 可以参考
专著, Davis 是老时间序列专家了. 一些综述可以在这里找到.
这篇我觉得证明很漂亮.
比较近的文章, 综述可以一看.
统计学更注重证明相关性质: 参数估计的相合性, 渐进正态性等.
在 深度需求预测 (Deep Demand Forecast) 中提到了几篇文章, 我看了作者关于 DeepAR 的 PyTorch 实现, 发现有明显的问题, 而且文章提到的一些 tricks 并没有实现. 后来看到了亚马逊的 gluonTS 包, 这里有一篇介绍 Neural time series models with GluonTS Time Series Workshop ICML 2019.
在 gluonTS 中, 其他深度时间序列的模型实现粗看都不如 deepar 的完整.
文档比较缺, 很多细节必须要读源码.