仓库源文，站点原文

title: "TPLinker 实体关系抽取以及 NER 变种" categories:

Machine Learning tags: NLP updated: 2022-01-30 comments: true mathjax: true

COLING 2020 的文章

Wang, Y., Yu, B., Zhang, Y., Liu, T., Zhu, H., & Sun, L. (2020). Tplinker: Single-stage joint extraction of entities and relations through token pair linking. arXiv preprint arXiv:2010.13415. [Code]

主要解决的问题: 两阶段方法中训练和推理阶段的数据分布不一致

实体关系抽取传统方法先抽取实体, 再预测实体对的关系 (分类问题). 这种两阶段方法无法考虑两个子任务之间的联系. 因此引入联合 (joint) 抽取, 即同时抽取实体和关系. 此外还要解决实体重叠问题 (同一个实体出现在多个三元组中).

大多数现有处理实体对重叠 (EntityPairOverlap, EPO) 和单实体重叠 (SingleEntiyOverlap, SEO) 的方法可分为两类:

基于解码器的模型使用编码器-解码器结构, 解码器每次抽取一个词或一个元组.
基于分解的模型先识别候选主语实体, 然后标注宾语实体和关系.

这些方法有共同的问题: 曝光偏差 (exposure bias). 编码器-解码器在训练阶段用了真实数据的 tokens, 但推理阶段用的是模型自己生成的 tokens. 因此训练和推理阶段用的数据来自不同分布. 基于分解的模型也有类似问题.

个人评价: 充其量是包装论文用的说法.

方法

TPLinker 是一个单阶段方法, 将联合抽取任务转化为 Token Pair Linking 问题.

TPLinker 其实非常简单粗暴, 标题就概括了它的方法: token pairs 的分类问题. 长度为 $n$ tokens 的序列中有顺序地取两个 tokens (可以取相同的), 记为 $p_1$ 和 $p_2$, 称为一个 token pair, 一共有 $n^2$ 个 token pairs. 对于每个 token pair 和每个关系 $r$, TPLinker 做三个独立的分类任务:

$p_1$ 和 $p_2$ 是否分别为同一个实体的开始和结束位置? 紫色: entity head to entity tail (EH-to-ET) 这个问题和关系 $r$ 无关.
$p_1$ 和 $p_2$ 是否分别为关系是 $r$ 的两个实体的开始位置? 红色: subject head to object head (SH-to-OH)
$p_1$ 和 $p_2$ 是否分别为关系是 $r$ 的两个实体的结束位置? 蓝色: subject tail to object tail (ST-to-OT)

几乎把所有的情况枚举了一遍, 当然理念上可以解决实体重叠问题.

无关紧要的细节

标注的实现

极其简单且无关紧要的细节, 把上述过程用矩阵表示, 其中 $n^2$ 个 token pairs 可以用 $n(n+1)/2$ 个数表示.

在矩阵中用 1 存储上述标签, 不同标签用不同矩阵.

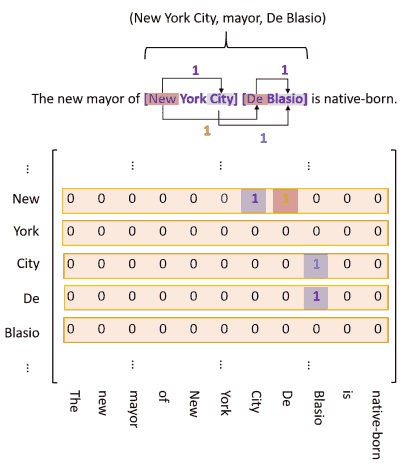
由于实体的尾部必然在头部后面, 所以对第一类标签, 矩阵左下三角都是 0, 可以舍去以节约内存. 而对另外两类标签, 宾语可能出现在主语前, 所以不能直接舍去矩阵左下角. 办法是把左下角的 1 翻到右上角, 存储为 2, 再把左下角舍去. 最后把矩阵摊平便于计算. (作者这里兜了圈子, 直接说在所有 token 对上标注就完事了, 1 是正向, 2 是反向.)

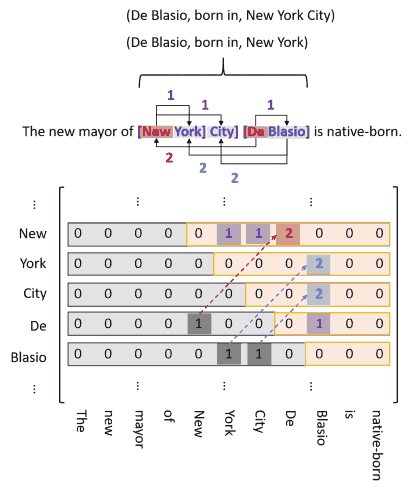
这样如上图可以自然地处理单实体重叠问题 (De Blasio 出现在两个三元组中). 为了解决实体对重叠问题, 需要对每一个关系都做序列标注. 如果有 $R$ 个关系, 就要做 $2R + 1$ 次序列标注 (第一类标签不涉及关系, 可以共用), 每个子任务生成长度为 $n(n+1)/2$ 的序列 (所有可能的 token pair 数), 其中 $n$ 为输入序列长度.

Handshaking tagger

很容易先得到所有的实体.
对每个关系 $r$, 做以下操作:
- 得到所有的 tail-to-tail token pairs $\mathcal T$.
- 对每一个 head-to-head token pair:
  - 对每一个以当前 subject head token 为起始的实体 $s$, 和每一个以当前 object head token 为起始的实体 $o$:
    - 如果 $s$ 到 $o$ 的 tail token pair 在 $\mathcal T$ 中, 则抽出三元组 $(s, r, o)$.

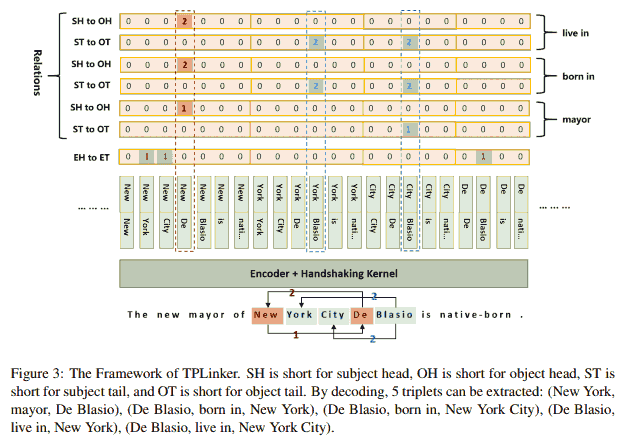
It seems that our tagging scheme is extremely inefficient because the length of the tagging sequence increases in a square number with increasing sentence length. Fortunately, our experiment reveals that by utilizing a lightweight tagging model on the top of the encoder, TPLinker can achieve competitive running efficiency compared with the state-of-the-art model, since the encoder is shared by all taggers (see Figure 3) and only needs to generate $n$ token representations for once.

BERT 是开销大头, 这个组件不影响速度.

The sequence is like the handshaking of all tokens, which is the reason why we refer to this scheme as the handshaking tagging scheme.

至少这个命名理由没有说服我. 下面是作者没有提及到的问题: 构造一个反例说明这个方案会出错的情况.

对于句子 ABCDEF, 三元组为 (AB, EF) 和 (ABC, DEF) 两个 (省略谓语, 只写主语宾语).

所有 tail-to-tail token pairs $\mathcal T$ 为 (B, F) 和 (C, F).
对于 head-to-head token pair (A, E):
- 考虑以 A 开头的主语 AB, ABC 和以 E 开头的宾语 EF, 因为 (B, F) 在 $\mathcal T$ 中, 抽取 (AB, EF).
对于 head-to-head token pair (A, D):
- 考虑主语 AB, ABC 和宾语 DEF, 因为 (B, F) 和 (C, F) 都在 $\mathcal T$ 中, 因此还会错误地抽取出 (AB, DEF).

实际上这种情况应该比较少, 而且最终是除了正确的三元组还会抽取多余的三元组.

顺便一提, 对于一篇 EMNLP 2021 文章

Ren, F., Zhang, L., Yin, S., Zhao, X., Liu, S., Li, B., & Liu, Y. (2021). A Novel Global Feature-Oriented Relational Triple Extraction Model based on Table Filling. arXiv Preprint arXiv:2109.06705.s

他主要是对 TPLinker 的基础上增加关于 relations 和 token pairs 的 "全局" 表格特征, 并相应提出了新的 tagging scheme (略), 它不能处理的情况如下

句子 ABCD 以 (A, D) (B, C) 为实体对时, 会抽取为错误的 (A, D) (B, C).
如果句子 ABCD 以 (A, C) (A, D) (B, C) (B, D) 为实体对时, 也会抽成 (A, D) (B, C).

这个方案可能抽取出错误的三元组或者少抽.

模型

分类问题的标准流程.

对一个长度为 $n$ 的句子 $[w_1, \dots, w_n]$, 先用 encoder 把每个 token $w_i$ 映射为向量 $c_i$, 然后用通常方法 (拼接输入向量, 线性变换后接激活函数) 生成 token pair $(w_i, w_j)$ 的表示

$$ h_{i, j} = \operatorname{tanh}\left(W_h [c_i, c_j] + b_h\right), \quad j\ge i, $$

其中 $W_h$ 和 $b_h$ 是训练参数.

之后是分类问题的通常方法 (线性变换后接 softmax 得到概率分布预测) 生成这个 token pair 的 link label (0, 1, 2) 的概率预测

$$ Y_{i,j} \sim \operatorname{softmax}(Wo h{i, j} + b_o). $$

上述操作对每个子任务都做一遍. 损失函数为对数极大似然

$$ L = - \frac1n \sum{t\in T} \sum{i=1}^n \sum{j\ge i}^n \log \mathbb P(Y^{(t)}{i, j} = l^{(t)}), $$

其中 $T$ 是序列标注全体子任务, $l^{(t)}$ 是对应子任务的真实 link label (0, 1, 2).

预测

$$ \operatorname{link}(w_i, w_j, t) = \operatorname{arg\,max}l \mathbb P(Y^{(t)}{i, j} = l). $$

具体实现的细节和效果

可以看到他把长度为 $n$ 的序列展成了 $\Theta(n^2)$ 的东西, 所以长度不能太大, 作者推荐不超过 100. 另外可以看到, 展开后这么长的序列里, 非 0 值很少, 矩阵非常稀疏.

对于超过最大长度的序列, 他的处理是, 用 sliding window 截取. 比如最大长度为 100, 每次划窗移动距离为 20, 则先取头 100 个 tokens 作为一个序列, 再取第 21~120 个 tokens 作为新的序列 (有关的实体关系对也要相应处理), 以此类推.

加速收敛的 trick: loss 可以看成实体识别和关系分类两个任务 loss 之和 (多任务学习). 先给实体识别更高的权重, 之后逐渐让其权重和关系分类持平. 经验上实体识别任务更简单, 并且对关系分类任务有一定指导作用, 可以加速收敛.
- 从网络设计上, 他并没有限制 head-to-head 的两头都存在以那个 token 为起始的实体, 所以先重视实体识别似乎有些道理.
构建数据集: 如果一个实体出现了复数次, 那么全部标注出来比较好.
有若干效果不好的报告 (f1 指标): 中文数据集上的效果探讨 0.6775, evaluating other datasets 0.6485, 自定义数据集上关系识别的效果很差, 我自己的数据集上大多收敛为 0.65 出头, 不到 0.7 (数据集太小? 标注质量低? 句子太长? 难度高? I have no idea.). 经验上 6k steps 后就拟合地差不多了.
- 在百度数据集上表现还可以. 估计是自己的数据集太小, 过拟合了.
代码比较乱, 一堆 jupyter notebooks, 代码里函数大量用全局变量.

衍生: TPLinker-NER

由于 TPLinker 做的是 token pairs 的分类, 显然它也可以做实体识别. TPLinker 是对每个 token pair 独立地做了 $2R+1$ 个分类问题, TPLinker-plus (原作者开发中的版本) 只做一个多标签分类问题, 具体参考苏剑林的推广, 也就是把 $n$ 选 1 的分类问题变成了 $n$ 选 $k$ 的分类问题. 有人用 TPLinker-plus 的这个子功能整理出了 TPLinker-NER, 并对中文数据集 CLUENER2020 做了验证, 据称效果还行 (用同样代码我还没复现出).

从发布时间上看, 他应该直接参考了苏剑林的 GlobalPointer, 用同样的数据集验证, 但好像没有实现后者的一些优化.