tags: [程序设计, 笔记, C++, '#NEED-UPDATE'] title: 哔哩哔哩 冒-_-泡 技术视频的笔记 last_modified_at: 2023-3-4 slug: bilibili-mao-pao-video-notes redirect_from:
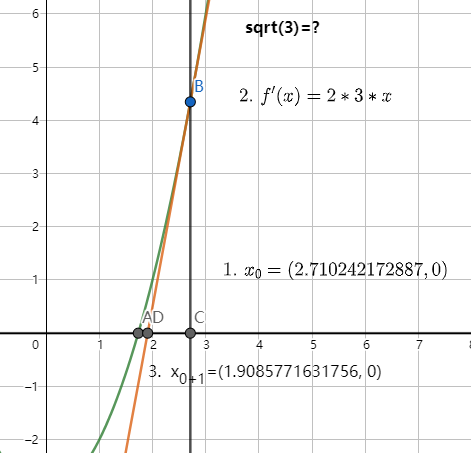
首先，我们要了解sqrt的原理：简而言之，就是先将$sqrt(a)=x$转换为求$x^2-a=0$的解。
具体来说，计算机会任取一个$x_0$，并求$x^2-a=0$在$x_0$上的切线（也就是导函数），通过该导函数与 x轴 的交点来逐渐逼近原函数的交点。多次重复以上过程，从而得到误差允许的解。（具体公式如下图）
其中，$x_{0+1}$点（也就是D点，或者说$x_1$点）的坐标可以化简为$(x_0+a/x_0)/2$（如果第一个值$x_0$为负数，也很容易看出$x_1$必定为正数）
那么，如何优化呢？若最开始取的$x_0$足够接近正解，我们就可以跳过大量运算。为此，我们要先了解一下 IEEE 754 浮点数规范
可以看到，浮点数是由指数与底数两部分分开存储。因此，我们只需要将指数先除 2，再将底数部分略微调整（此处通过多次实验，可以得出最优底数调整值），即可得到非常近似的结果。
具体代码参看原视频12:55处，摘录如下：
float mySqrt(float x){
float a = x;
unsigned int* p = (unsigned int*)&x; // 用于进行位的运算
*p = (*p + 0x3f76cf62) >> 1; // 魔数推导详见视频，通过大量随机测试得到结果
x = (x + a / x) / 2; // 前文所述的逼近正解，这句可以复制多次以更大减小误差
return x;
}
建模：以一个一维数组表示每行皇后的位置
搜索树：搜索+剪枝，找到合法状态
前提：约束满足问题（CSP）：在若干变量的情况下，要求找到一组满足约束的解
原因：传统搜索深度与 n 成指数关系，效率低，且目的是统计所有状态
性质：随机化算法，每次得到的解可能不同
联系：模拟退火；局部剪枝；弧相容技术
状态空间：n 行所有可能性
状态变迁：某行皇后位置的迁移
若两个状态能通过一次迁移得到，则认为它们是连接的
状态价值评估：冲突数量，冲突越少则目前状态价值越高
多次随机选择起点，通过不断迁移找到更好的解（局部贪心搜索），找到正解或局部最优解后本次搜索结束
若找到的是局部最优解（本身有冲突，且无论如何迁移都会冲突），则随机起点重新搜索
效率：由于是单向搜索（只像价值较高状态搜索），效率较高
状态空间：n 行不同列的排列
状态变迁：某两个皇后所在行的交换
状态价值评估：冲突数量（仅需考虑斜线）
效果：状态空间：$n^n$ -> $n!$
strcmp随机输入时，标准库中的strcmp远比手动实现的慢。为什么？
其中一个原因，可能是strcmp存在硬件优化，由于进行大范围的读取而导致效率降低；但手工实现的是逐个字符比较的，在第一处不同就会直接返回，不会出现大规模复制问题。
那随机字符串比较的平均时间复杂度是？或者说，找到第一处不相等的字符需要几次比较？
不懂，请自行跳转原视频08:09查看
$E=(c-1)/c+(1/c)*(1+E)$
其中c代表每个字符可取的值的数量，E代表最终比较数的期望值，本方程的思想就是设字符串无限长，将第一个字符相等与第一个字符不相等的总值相加，解得$E=c/(c-1)$；当c较大（比如 255）时，平均时间复杂度就约为O(1)
最坏时间复杂度O(MN)，平均时间复杂度O(N)（输入随机）（参考：《算法导论》），也是 Java 的实现算法
需要预处理，在极端情况下可能更慢，而朴素算法相对较通用；同时，作为基础库要保证代码维护性
根据视频的描述，该 hash 算法是在 Java 中对字符串求 hashCode的算法的一种实现。具体来说，它将字符串视作类似 31 进制求值（若溢出则直接回环），近似公式如下（与真正代码很不同）：
$str.hashCode() == (\sum_{i=0}^{str.length}str[i]*31^i) \% 2^N$
注意，这里的 B 不一定要选 31,但最好不要选 2 的倍数。由于执行时会对$2^N$取模，因此若字符串很长，前半段就无法参与运算。
对 100 万以内所有数字取 hash，可以发现，以字符串形式存储数字不会产生 hash 冲突，但以大端序整数存储数字冲突率极高（约每 40 个数字会有相同的 hash）
以0xbd4与0xaf3为例，(b-a)^31 = 1^31 = 31^1 = (0xf3-0xd4)^1，也就是说后两位的哈希值经过累计抵消了最高位的的哈希差。然而，在 ASCII 码中几乎不可能出现此情景，因此以字符串形式存储不会有这种冲突。
那么，如何解决？显而易见，只要低位的差远远小于模数，就不会发生这种冲突（可以理解为不会进位）。因此，将模数由 31 调整为 60001 一类的数，就可以解决此问题。
目前的算法中，如果最后一次参与加法的位是连续的，那么计算出来的 hash 值也是连续的，会造成一定效率问题。对此，需要乘法打散：即将最后得到的 hash 值再次乘以一个相对较大的数（如 60001），以防止所有 hash 值完全连续
如果最早参加乘法的数位数值上均为 0，那无论有多少个 0，hash 值都是相同的。对此，可以将运算时的初值由 0 改为 1（也就相当于上方简介中的公式），这样前导零会被视为普通的数值参与运算。
<del>历史遗留</del> 在随机生成数据的场景下已经有较好的表现了，但并不完善。生产环境下建议自己重新实现。